* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Production Function - National Bureau of Economic Research
Survey
Document related concepts
Transcript
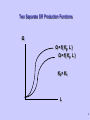
Production Function Qt=ƒ(inputst) Qt=output rate inputt=input rate where is technology? Production Function Q=ƒ(Kt,Lt) Qt Kt Firms try to be on the surface of the PF. Inside the function implies there is waste, or technological inefficiency. Lt 1 Difference between LR and SR LR is time period where all inputs can be varied. Labor, land, capital, entrepreneurial effort, etc. SR is time period when at least some inputs are fixed. Usually think of capital (i.e., plant size) as the fixed input, and labor as the variable input. 2 LR production function as many SR production functions. Long Run: Q = f (K,L) Suppose there are two different sized plants, K1 and K2. One Short Run: Q = f ( K1,L) i.e., K fixed at K1 A second Short Run: Q = f ( K2,L) i.e., K fixed at K2 Show this graphically 3 Two Separate SR Production Functions Q Q = f( K2, L ) Q = f( K1, L ) K2 > K1 L 4 What Happens when Technology Changes? This shifts the entire production function, both in the SR and in the LR. Technology Changes Q TP after computer TP before computer L 6 SR Production Function in More Detail Express this in two dimensions, L and Q, since K is fixed. Define Marginal Product of Labor. Slope is MPL=dQ/dL Identify three ranges Qt=ƒ(Kfixed,Lt) I II III Q I: MPL >0 and rising II: MPL >0 and falling III: MPL<0 and falling L 7 Where Diminishing Returns Sets In As you add more and more variable inputs to fixed inputs, eventually marginal productivity begins to fall. As you move into zone II, diminishing returns sets in! Why does this occur? Q I II L 8 Why Diminishing Returns Sets In Since plant size (i.e., capital) is fixed, labor has to start competing for the fixed capital. Even though Q still increases with L for a while, the change in Q is smaller. Q I II L 9 Define APL and MPL Average Product = Q / L output per unit of labor. frequently reported in press. Marginal Product = dQ/dL output attributable to last unit of labor used. what economists think of. 10 Average Productivity Graphically Take ray from origin to the SR production function. Derive slope of that ray Q=Q1 L=L1 Thus, Q/L =Q1 /L1 Q Q=f(KFIXED,L) Q1 Q L L1 L 11 Average Productivity Graphically APL rises until L2 Beyond L2 , the APL begins to fall. That is, the average productivity rises, reaches a peak, and then declines Q Q=f(KFIXED,L) Q2 Q/L L L2 APL L2 12 Average & Marginal Productivity There is a relationship between the productivity of the average worker, and the productivity of the marginal worker. Think of a batting average. Think of your marginal productivity in the most recent game. Think of average productivity from beginning of year. When MP > AP, then AP is RISING When MP < AP, then AP is FALLING When MP = AP, then AP is at its MAX 13 Average Productivity Graphically Q MPL rises until L1 Beyond L1 , the MPL begins to fall. Look at AP i. Until L2, MPL >APL and thus APL rises. ii. At L2, MPL=APL and thus APL peaks. iii. Beyond L2, MPL<APL and thus APL falls. L1 L L2 Q/L MPL L1 L2 APL 14 Intuitive explanation Anytime you add a marginal unit to an average unit, it either pulls the average up, keeps it the same, or pulls it down. When MP > AP, then AP is rising since it pulls it the average up. When MP < AP, then AP is falling since it pulls the average down. When MP = AP, then AP stays the same. Think of softball batting average example. 15 LR Production Function Qt Kt Isoquants (i.e.,constant quantity) Lt 16 Define Isoquant Different combinations of Kt and Lt which generate the same level of output, Qt. Isoquants & LR Production Functions ISOQUANT MAP Qt = Q(Kt, Lt) Output rate increases as you move to higher isoquants. Slope represents ability to tradeoff inputs while holding output constant. K Marginal Rate of Technical Substitution. Closeness represents steepness of production hill. Q3 Q2 Q1 L 18 Slope of Isoquant Slope is typically not constant. Tradeoff between K and L depends on level of each. Can derive slope by totally differentiating the LR production function. Marginal rate of technical substitution is –MPL/MPK Kt Q Lt 19 Extreme Cases No Substitutability Perfect Substitutability K K Q2 Q Q1 2 Q1 L Inputs used in fixed proportions! L Tradeoff is constant 20 Substitutability Low Substitutability High Substitutability K K Q1 Q1 L Slope of Isoquant changes a lot L Slope of Isoquant changes very little 21 Isoquants and Returns to Scale Returns to scale are cost savings associated with a firm getting larger. Increasing Returns to Scale Production hill is rising quickly. Lines on the contour map get closer with equal increments in Q. K Q=40 Q=30 Q=20 Q=10 L 23 Decreasing Returns to Scale Production hill is rising slowly. Lines on the contour map get further apart with equal increments in Q. K Q=40 Q=30 Q=20 Q=10 L 24 How Can You Tell if a PF has IRS, DRS, or CRS? It is possible that it has all three, along various ranges of production. However, you can also look at a special kind of function, called a homogeneous function. Degree of homogeneity is an indicator returns to scale. 25 Homogeneous Functions of Degree A function is homogeneous of degree k if multiplying all inputs by , increases the dependent variable by Q = f ( K, L) So, • Q = f(K, L) is homogenous of degree k. Cobb-Douglas Production Functions are homogeneous of degree + 26 Cobb-Douglas Production Functions Q=A•K •L is a Cobb-Douglas Production Function Degree of Homogeneity is derived by increasing all the inputs by = A • ( K) • ( L) Q = A • K • L Q = A • K • L Q 27 Cobb-Douglas Production Functions This is a Constant Elasticity Function Elasticity of substitution s = 1 Coefficients are elasticities is the capital elasticity of output, EK is the labor elasticity of output, E L If Ek or L <1 then that input is subject to Diminishing Returns. C-D PF can be IRS, DRS or CRS if + 1, then CRS if + < 1, then DRS if + > 1, then IRS 28 Technical Change in LR Technical change causes isoquants to shift inward Less inputs for given output May cause slope to change along ray from origin Labor saving Capital saving May not change slope Neutral implies parallel shift 29 Technical change Labor Saving Capital Saving K K L L 30 Lets now turn to the Cost Side What is Goal of Firm? Define Isocost Line Put K on vertical axis, and L on horizontal axis. Assume input prices for labor (i.e., w) and capital (i.e., r) are fixed. Define: TC=w*L + r*K Solve for K: r*K= TC-w*L K=(TC/r) - (w/r)*L Isocost Line K TC/r Slope=-w/r L 32 TC constant along Isocost line. K TC1/r L TC1/w 33 in TC parallel shifts Isocost K TC2/r TC2 > TC1 TC1/r L TC1/w TC2/w 34 Change in input price rotates Isocost K w2 < w1 TC/r L TC/w1 TC/w2 35 Optimal Input Levels in LR Suppose Optimal Output level is determined (Q1). Suppose w and r fixed. What is least costly way to produce Q1? K Q1 L 36 Optimal Input Levels in LR Suppose Optimal Output level is determined (Q1). Suppose w and r fixed. What is least costly way to produce Q1? Find closest isocost line to origin! K Optimal point is point of allocative efficiency. K1 Q1 L1 L 37 Cost Minimizing Condition Slopes of Isoquant and Isocost are equal Slope of Isoquant=MRTS=- MPL/ MPK Slope of Isocost=input price ratio=-w/r At tangency, - MPL/ MPK = -w/r Rearranging gives: MPL/w= MPK /r In words: Additional output from last $ spent on L = additional output from last $ spent on K. 38 The LR Expansion Path Costs increase when output increases in LR! Look at increase from Q1 to Q2. Both Labor and Capital adjust. Connecting these points gives the expansion path. K expansion path K2 K1 Q2 Q1 L L1 L2 39 We can show that LR adjustment along the expansion path is less costly than SR adjustment holding K fixed! Start at an original LR equilibrium (i.e., at Q1). K K1 Q1 L L1 41 LR Adjustment LR adjustment: K increases (K1 to K2) L increases (L1 to L2) TC increases from black to blue isocost. K K2 K1 Q2 Q1 L1 L2 L 42 SR Adjustment SR adjustment. K constant at K1. L increases (L1 to L3) TC increases from black to white isocost. K K1 Q2 Q1 L1 L3 L 43 LR Adjustment less Costly White Isocost (i.e., SR) is further from the origin than the Blue Isocost (LR). Thus, the more flexible LR is less costly than the less flexible SR. K K2 K1 Q2 Q1 L1 L2 L3 L 44 Impact of Input Price Change Start at equilibrium. Recall slope of isocost=K/L= -w/r Suppose w and optimal Q stays same (i.e., Q1) Rotate budget line out, and then shift back inward! K Q1 K1 L1 L 45 Decrease in wage leads to substitution Firms substitute away from capital (K1 to K2). Firms substitute toward labor (L1 to L2) Pure substitution effect: a to b Maps out demand for labor curve K a K1 b K2 Q1 L1 L2 L 46 Derivation of Labor Demand from Substitution Effect Wage falls w K w1 a K1 w2 b K2 Q1 L1 L2 DL1 L L1 L2 L 47 There is also a scale effect Scale effect is increase in output that results from lower costs Scale effect: b-c K Q1 Q2 a K1 c b L1 L 48 Scale Effect Shifts Demand Wage falls w K w1 K1 c a w2 b K2 DL2 Q1 L1 L2 L3 DL1 L L1 L2 L3 L 49 Recall the Isocost Line TC=w*L + r*K Thus, TC=TVC+TFC Lets relate the cost relationships to the production relationships. Recall the Law of Diminishing Returns. 50 Law of Diminishing Marginal Returns As you add more and more variable inputs (L) to your fixed inputs (K), marginal additions to output eventually fall (i.e., MPL= Q/L falls) What does this say about the shape of cost curves? 51 Marginal Productivity (MPL) and Marginal Cost (MC) Look at how TC changes when output changes. Assume w and r are fixed. Since TC=w*L+r*K then TC = w*L + r*K How does K change in SR? 52 Changes in TC in SR must come from changes in Labor. TC = w* L Divide through by change in Q (ie. Q) TC/Q = w* (L/Q) TC/Q = Marginal Cost = MC What is MPL? MPL=(Q/L) Thus: TC/Q = w* 1/(Q/L) This gives: MC=w/MPL 53 MC=w/MPL Look at where Diminishing Returns sets in. MC MPL MPL L1 L Q 54 MC=w/MPL Substitute L1 into SR Production Function Q1=f(KFIXED,L1) MC MPL MC MPL L1 L Q1 Q 55 Alternatively: TC and TP Substitute L1 into SR Production Function Q1=f(KFIXED,L1) TC Q TC MPL L1 L Q1 Q 56 Relationship between APL and AVC TC=TVC + TFC TC = w*L + r*K Divide equation by Q to get average cost formula. TC/Q = w*L/Q + r*K/Q ATC = AVC + AFC Thus, AVC=w*L/Q 57 AVC and APL AVC=w*L/Q Rearranging: AVC=w/(Q/L) Since Q/L=APL AVC=w/APL Diagram is similar. 58 AVC=w/APL Substitute L2 into SR Production Function Q2=f(KFIXED,L2) APL AVC AVC APL L2 L Q2 Q 59 Put SR Cost Curves Together Average Cost Curves ATC $ AVC AFC Q 61 Short Run Average Costs and Marginal Cost $ ATC MC AVC Q 62 Cost Curve Shifters (Variable Cost Increases) A change in the wage shifts the AVC and MC curves. Thus, the ATC curve also shifts upward. MC’ ATC’ $ AVC’ ATC AVC MC Q 63 Cost Curve Shifters (Fixed Cost Increases) An increase in price of capital increases fixed costs, but not variable costs. Thus, AVC and MC are fixed, but ATC increases. $ ATC’ MC ATC AVC Q 64 Costs in the LR Why did SR cost curves have the shape they did? Why do LR cost curves have the shape they do? 65 LR Total Costs Graphically TC Cost CRS DRS IRS Q 66 Why are there Economies of Scale? Specialization in use of inputs. Less than proportionate materials use as plant size increase. Some technologies are not feasible at small scales. 67 Why do Diseconomies of Scale Set In? Eventually, large scale operations become more costly to operate (i.e., they use more resources) due to problems of coordination and control. e.g., red tape in the bureaucracy. Graphical Representation 68 Economies and Diseconomies of Scale Assume Q increases 10 units for each isoquant K IRS L 69 Economies and Diseconomies of Scale Assume Q increases 10 units for each isoquant K DRS IRS L 70 Economies and Diseconomies of Scale LRAC curve Assume Q increases 10 units for each isoquant K $ DRS DRS IRS CRS CRS IRS L QMES Q 71 LRMC and LRAC Curves LRAC and LRMC LRMC is TC/Q (i.e., change in TC from a change in Q) when all inputs are variable inputs. When LRMC is above LRAC, it pulls the average up, and viceversa. $ LRMC LRAC Q 73 Relating SR to LR curves Relationship between SR ATC and LRAC curves. At Q1, the SR plant size which gives ATC1 is least costly. $ ATC1 LRAC Q Q1 75 Relationship between SR ATC and LRAC curves. At Q1, the SR plant size which gives ATC1 is least costly. SR ATC is tangent to LRAC at one point. $ ATC1 LRAC Q Q1 76 Relationship between SR ATC and LRAC curves. $ ATC1 LRAC At Q1, the SR plant size which gives ATC1 is least costly. SR ATC is tangent to LRAC at one point. Tangency is not at minimum point of ATC1. Q Q1 77 Adjustments in SR are still more costly than LR At Q2, the SR plant size which gives ATC1 is no longer least costly. $ ATC1 LRAC atc1 lrac1 Q Q2 78 Adjustments in SR are still more costly than LR At Q2, the SR plant size which gives ATC1 is no longer least costly. Optimal move would be to larger plant size! $ ATC1 LRAC atc1 lrac1 Q Q2 79 LRAC is lower “envelope” of family of SRATC curves $ ATC1 ATC2 ATC3 LRAC Q Q1 Q2=QMES Q3 80 SRMC and LRMC $ LRMC SRMC1 SRMC3 SRMC2 LRAC SRATC3 SRATC1 SRATC2 q1 q2 q3 q 81