* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Pricing I: Linear Demand - Management By The Numbers
Pricing science wikipedia , lookup
Revenue management wikipedia , lookup
Yield management wikipedia , lookup
Service parts pricing wikipedia , lookup
Gasoline and diesel usage and pricing wikipedia , lookup
Dumping (pricing policy) wikipedia , lookup
Perfect competition wikipedia , lookup
Pricing strategies wikipedia , lookup
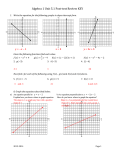
Pricing I: Linear Demand This module covers the relationships between price and quantity, maximum willing to buy, maximum reservation price, profit maximizing price, and price elasticity, assuming a linear relationship between price and demand. Authors: Paul Farris and Phil Pfeifer Marketing Metrics Reference: Chapter 7 © 2010-14 Paul Farris, Phil Pfeifer and Management by the Numbers, Inc. Definition Linear demand functions are those in which the relationship between quantity and price is linear. This means that any identical change in price (no matter what the starting price) produces an identical change in units demanded. The per unit change in Q caused by a change in P is called the slope. With linear demand “curves”, the slope is constant (the same for all prices). The demand “curve” is actually a demand “line”. LINEAR PRICE-QUANTITY FUNCTIONS Linear Price-Quantity Functions This presentation covers the topics of maximum willing to buy (MWB), maximum reservation price (MRP), profit maximizing price, and price elasticity under the assumption of a linear relationship between price and quantity. MBTN | Management by the Numbers 2 Increasing price from $0.50 to $1.50 causes a drop in quantity from 9 to 7 units. Thus, the slope (delta Q / delta P) is – 2 = (9 – 7) / (1.5 –.50). 10 9 8 7 Quantity 6 5 4 3 2 1 0 Increasing price from $2 to $3 causes a drop in quantity from 6 to 4. Thus, the slope (delta Q / delta P) is also -2, for each $1 change in price we see a change on 2 unit of quantity sold in the opposite direction. 0 $1 $2 Price $3 $4 $5 LINEAR PRICE-QUANTITY DEMAND Linear Price-Quantity Demand Insight Price slope is almost always negative, but often people drop the sign. Definition Slope of demand = change in quantity / change in price. 3 MWB is where P = 0 MWB -- Maximum Willing to Buy 10 9 8 7 Quantity 6 5 4 3 2 1 0 Formulas for linear demand functions use the following format (recall y = mx + b): Quantity = Slope * Price + MWB In this example, beta = - 2. One could then solve for MWB and MRP using this equation and a price quantity point. MRP -- Maximum Reservation Price 0 $1 $2 Price $3 $4 LINEAR PRICE-QUANTITY DEMAND FORMULA Linear Price-Quantity Demand Formula $5 MRP is where Q = 0. MBTN | Management by the Numbers 4 Definitions Maximum Willingness to Buy (MWB) = Quantity - Slope * Price Conceptually, MWB is the quantity that would be sold (presuming linear demand) if the price is free (price = 0). Maximum Reservation Price (MRP) = MWB / (- Slope) Conceptually, MRP is the maximum price where some quantity would be sold (again, presuming linear demand). This is actually where the linear demand line crosses the axis or where quantity = 0. LINEAR PRICE-QUANTITY DEMAND FORMULA Linear Price-Quantity Demand Formula We took a bit of a leap of faith there. For some of you, it may be helpful to review the how these formulas were derived which we’ll do on the following slide. MBTN | Management by the Numbers 5 You may recall from algebra that linear functions follow the format: y = mx + b Where b is the Y intercept (where the line crosses the y axis or where x = 0), m is the slope of the line, and x and y are the coordinates of any point on the line. First, let’s express the basic linear function using marketing terminology: Quantity = Slope * Price + MWB We can use this basic equation for price / quantity relationships as well as bringing in some other important managerial concepts such as the maximum willingness to buy (MWB) and maximum reservation price (MRP). With a little substitution, the equation is, Quantity = MWB * [1 – Price / MRP] LINEAR PRICE-QUANTITY DEMAND FORMULA Linear Price-Quantity Demand Formula From this, we can derive functions solving for MWB and MRP in the definitions. Definitions Maximum Willingness to Buy (MWB) Maximum Reservation Price (MRP) = Quantity - Slope * Price = MWB / (- Slope) MBTN | Management by the Numbers 6 Now let’s turn to the question of maximizing profit using the following example. MWB 10 9 8 7 Quantity 6 5 4 3 2 1 0 If you are told that the unit cost is $1, what is the optimal (profitmaximizing) price to charge? OPTIMAL (PROFIT MAXIMIZING) PRICE Optimal (Profit Maximizing) Price MRP 0 $1 $2 Price $3 $4 $5 Unit Cost MBTN | Management by the Numbers 7 Answer As you might expect, the profit maximizing price is always more than cost and less than the MRP. MWB 10 9 8 7 6 Quantity 5 4 3 2 1 0 But, it is nice, and maybe a little surprising, that the profit-maximizing price is ALWAYS exactly half-way between unit costs and MRP. Profit = Q * (P-C) = 4 * ($3-$1) = $8 0 $1 $2 Price $3 OPTIMAL (PROFIT MAXIMIZING) PRICE Optimal (Profit Maximizing) Price MRP $4 $5 C = Unit Cost, P = Price, Q = Quantity MBTN | Management by the Numbers 8 So, for linear demand functions, we only need two pieces of information to calculate the profit maximizing price: 1. Unit Variable Cost and 2. Maximum Reservation Price (MRP is where Q is equal to 0) BIG CONCLUSION! Big Conclusion! Definition Profit Maximizing Price = ½ (Unit Cost + MRP) In addition, since linear demand functions have a constant slope, with any two points (price quantity combinations) you can calculate the slope, the MWB, and the MRP. Now let’s apply these definitions in a couple of examples. Question 1: For a product, we observe that at a price of $5, a quantity of 8 is sold and that at $4 we sell 12 units of a product. The cost of the product is $3. What is the MWB, MRP and Profit Maximizing Price? MBTN | Management by the Numbers 9 First, we have two data points, necessary to calculate the slope which we’ll need for solving for MWB. Slope = delta Q / delta P = (8 – 12) / (5 – 4) = – 4 Using the MWB = Quantity - Slope * Price formula, substitute one set of price & quantity values from above along with the slope. MWB = 12 – (-4 * 4) MWB = 12 – (-16) = 12 + 16 = 28 Verify with the other point: MWB = 8 – (-4 * 5) = 8 + 20 = 28 (Matches) Now, it is easy to find MRP by solving for the price at which we sell zero units. 0 = 28 – 4 * price = $7 or by using MRP = MWB / (- Slope) MRP = 28 / - (-4) = 28 / 4 = $7 EXAMPLE OF HOW TO CALCULATE MWB AND MRP Example - How to Calculate MWB & MRP Profit Maximizing Price = 1/2 (Cost + MRP) = ½ (3 + 7) = $5. Answers: MBW = 28, MRP = $7, Profit Maximizing Price = $5 MBTN | Management by the Numbers 10 Question 2: Suppose we apply regression to sales data, and find the following demand function where slope = – 4 and MWB = 100: q = slope * p + MWB = – 4 * p + 100 If the unit cost equals $5, what is the optimal price? Answer: First, find MRP by dividing MWB by – slope (e.g. a + value), 100 / 4 = 25, so MRP = 25 FINDING OPTIMAL PRICE WITH REGRESSION Finding Optimal Price with Regression Then add to the cost ½ the difference between cost and MRP. Cost + ½ (MRP – Cost) = $5 + ½ ($25 – $5) = $15 So, the profit-maximizing price is $15. MBTN | Management by the Numbers 11 The slope is the unit change in quantity for a small unit change in price. For linear demand curves, the slope is constant (the same at all prices). Another measure of how “much” quantity reacts to changing prices is ELASTICITY. Whereas slope is a unit per unit change rate, elasticity is a percentage per percentage change rate. It is the slope times (P/Q), and is often thought of as the percentage change in Q for a small percentage change in P. MBTN | Management by the Numbers SLOPE VERSUS ELASTICITY Slope versus Elasticity 12 For a linear demand curve, the slope is a constant. This means that the elasticity will NOT be a constant but will depend on the initial price. For any linear demand curve, the elasticity is larger for higher prices. This makes sense because if a unit change in price produces a constant unit change in Q, the unit increase in price is a smaller percentage of P if P is high and the unit decrease in Q is a larger percentage of Q when Q is low (which it is if P is high). MBTN | Management by the Numbers SLOPE VERSUS ELASTICITY Slope versus Elasticity 13 Increasing price from $0.50 to $1.50 causes a drop in quantity from 9 to 7 units. Thus, the slope (delta Q / delta P) is 2 and the elasticity (– 2 / 9) / ($1 / $0.5) = –.11 10 9 8 7 Q 6 5 4 3 2 1 0 Increasing price from $2 to $3 causes a drop in quantity from 6 to 4. Thus, the slope (delta Q/delta P) is 2, but the elasticity is (– 2 / 6) / ($1 / $2) = –.67 0 $1 $2 $3 Note that if we calculate the elasticity for the same interval using a decrease in price from $3 to $2, we get (2 / 4) / (– $1 / $3) = –1.5, a different value. $4 $5 LINEAR PRICE-QUANTITY DEMAND Linear Price-Quantity Demand Price Insight For linear demand functions, elasticity changes at each point on the price-quantity demand function. MBTN | Management by the Numbers 14 Example: Using the formula, q = – 4 * p + 100, calculate the price elasticity at the point where p = $15, the profit-maximizing price. • First, calculate q = – 4 * 15 + 100 = 40 • Next, the price elasticity is equal to the slope * p / q = – 4 * (15 / 40) = – 1.5 • Now calculate the percentage margin on selling price at profitmaximizing price…($15 - $5) / $15 = 66.7% • Divide the margin into 1 = 1 / .667 = 1.5 • At the profit maximizing price, the elasticity is equal to the reciprocal of the margin and vice versa. The minus sign is ignored for these purposes. This is a very powerful and important result that always holds, regardless of the nature of the form of demand. PRICE ELASTICITY AND OPTIMAL MARGIN Price Elasticity and Optimal Margin Definition At the Profit Maximizing Price: Elasticity = 1 / Margin%, and Margin% = 1 / Elasticity. MBTN | Management by the Numbers 15 When selling through resellers, we still need to calculate the MRP in terms of retail price, but now we have the added complication of the channel margins impacting the margin calculation. Since, retailers often require a percentage* margin, it is no longer a constant dollar variable cost as price changes. One way to handle this is to use the retail margin to convert Retail MRP to the Marketer MRP. Let’s use the linear demand function below to illustrate. SELLING THROUGH RESELLERS Selling Through Resellers Example: Q = – 4 * Retail Price + 100 and assume retailers earn a 40% margin and that unit costs are $5. First, calculate MRP = MWB/4 = 100/4 = $25 (Retail) Since retailers take 40% margins, our marketer only receives 60% of retail price. For her profit calculations, the MRP (Marketer) = $25 * 60% = $15. Maximum profit is earned at the Marketer price that is halfway between $15 and $5, or $10. This corresponds to a Retailer Price of $16.66 ($10/.6). * If retailers use constant dollar margins, we could just add that dollar margin to our unit variable cost. MBTN | Management by the Numbers 16 Although price elasticity is not very useful if the demand function is linear, elasticity is the key to finding the optimal price for nonlinear demand curves. As we just observed, at the optimal price, the elasticity is always equal to the reciprocal of the margin (or vice versa) if the sign is dropped. We can easily verify this for our linear example. MORE ON PRICE ELASTICITY More on Price Elasticity In Pricing II – Constant Elasticity, we will examine demand curves that are not linear. For non-linear demand curves, it will not be as easy to find the optimal price. However, what we can do is compare the elasticity (if we know it at the current price) to the reciprocal of our current margin. If they are not equal, we know which direction to adjust our price to improve profit. Eventually, these adjustments will lead to the optimal price. MBTN | Management by the Numbers 17 Marketing Metrics by Farris, Bendle, Pfeifer and Reibstein, 2nd edition, chapter 7. - And the following MBTN modules - FURTHER REFERENCE Further Reference Pricing II: Constant Elasticity - This module explores pricing under the assumption of demand curves that are not linear. Profit Dynamics - This module is a more basic module that examines price-volume trade-offs. Promotion Profitability - This module examines the role of promotion in pricing decisions. MBTN | Management by the Numbers 18