* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Mathematical Models in Molecular Biology
Mathematical physics wikipedia , lookup
History of numerical weather prediction wikipedia , lookup
Computational fluid dynamics wikipedia , lookup
Mathematical economics wikipedia , lookup
Numerical weather prediction wikipedia , lookup
General circulation model wikipedia , lookup
Theoretical ecology wikipedia , lookup
Theoretical computer science wikipedia , lookup
Natural computing wikipedia , lookup
Computational phylogenetics wikipedia , lookup
Mathematical Models in Molecular Biology
Harvey J. Greenberg
and
William L. Briggs
Mathematics Department
University of Colorado at Denver
What purpose does a mathematical model serve?
Insight
– Identifying crucial dependencies
– Understanding dynamics
– Interaction effects
Finding “best” experiments
– Guide to the most information for least cost ($, time)
– Learning (feedback) paradigm
Ability to predict in silico
– Fundamental use of models
– Quality could be relative, rather than absolute
(measuring change could be accurate even if both predictions are off)
Some History
Genetics – Statistics (Mendel, 1866)
Population Genetics – Differential & difference eqns.
(Fisher, Wright, Sewall, 1920s)
Epidemiology – Differential eqns, statistics (1950s)
Neurology – Networks (McCulloch-Pitts, 1943),
Partial Differential eqns (Hodgkin-Huxley, 1952)
DNA segments & cloning – Graph theory (Benzer, 1959)
Human Genome Project
Genome for E. coli (1997)
– 4.7 million base pairs
Human genome published (2001)
– 3 billion base pairs
Exponential Growth in Databases
Protein Data Bank
GenBank
Databases doubling less than every 18 months
(Defies Moore’s Law for growth of computer power)
Birth of a New Field
from Inevitable Marriage of Mathematics,
Computer Science, and Biosciences
Surge of data and computer power
Bioinformatics/Computational (Molecular) Biology
Math.
Models
Problems
Sequencing
Homology
Phylogenetics
Assembly
Gene finding
Gene mapping
Structure recognition
Structure prediction
Pathway inference
&
Comp.
Methods
Graph theory
Combinatorics
Differential equations
Dynamical systems
Information theory
Neural networks
Optimization
Probability
Statistics
… much more
in vivo in vitro in silico
C
o
m
p
u
t
e
r
S
c
i
e
n
c
e
So much to learn!
Life
Biochemistry
DNA/RNA
Evolution
Organisms
Genes
Cells
Genomics
Proteomics
Instruments
Opportunities galore!
Alignment Models
What
DNA – fragments, chromosomes, genes
RNA – coils, sheets, turns
Proteins – sequences, structures
How
Minimizing edit distance
Maximizing similarity
(used by BLAST for database searches)
DNA Alignment
Simplistic distance measure = # replacements:
GCTACTG
CGTCACT
D=6
Other evolutionary events – insertion/deletion: – GCTACTG
CGTCACT–
D = 2 + 2i
– reversal:
– GCT ACTG
CG TC ACT–
D = 2i + r
More evolutionary events can be accounted for with more complex
mathematical scoring, leading to challenges in algorithm design.
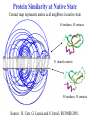
Protein Similarity at Native State
Contact map represents amino acid neighbors in native state
44 residues; 43 contacts
31 shared contacts
58 residues; 53 contacts
Source: R. Carr, G. Lancia and S. Istrail, RCOMB 2001.
Protein Folding
Predict
Primary Structure
= Sequence of amino acids
Tertiary Structure
= Folded protein (native state)
Lattice Model
Hydrophobic
Hydrophilic
hydrophobic contact
Score = # hydrophobic contacts
Grossly oversimplified – yes, but
biology insights from surprise folds, not from best predictions
NP-hard – yes, but
approximation algorithms getting better
Mathematically complex – yes, but
new approaches under development (e.g., symmetry exclusion)
Phylogenetic Trees
Goal: understand evolutionary relations
(any scale – species to genes)
Models & Methods:
Hierarchical clustering (of sequences)
Maximum likelihood
Maximum parsimony
Phylogenetic tree of placental
Campbell & Heyer
mammals with a marsupial as
the root. This tree used the 2,947 bp
nuclear sequences, which were available
for a wider range of species than the
longer 5,808 bp sequences (mixture of
nuclear and mitochondrial sequences).
The letters at each branch point indicate
a decreasing likelihood with “a” being
the most likely rating. Blue arrow
highlights the location of the human
branch.
Source: A.M. Campbell & L.J. Heyer
Discovering Genomics, Proteomics,
& Bioinformatics, 2003
example
Pathway Inference
Importance
Discover cause of disease
Find drug targets
Predict drug side effects
Find optimal drug dose
Reduce animal models needed for testing
Mathematical Methods
Boolean networks/Finite state machines
Linear programming/Stoichiometry
Logical/Integer programming
Graph theory
Differential equations
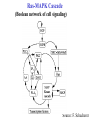
Ras-MAPK Cascade
(Boolean network of cell signaling)
Source: F. Schacherer
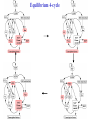
Equilibrium 4-cycle
ODE Models
S-systems
dS
Vmax S
dP
— = – ———— = – —
dt
KM + S
dt
Flux-Balance Analysis (FBA)
dx
— = Av – b
dt
Generalized Mass Action (GMA)
dxi
— = rik xj fijk
dt
k
j
Optimization Models
Objectives to set phenotype range:
• maximize growth
• minimize by-product production
• minimize mass nutrient uptake
Objectives to filtering pathways:
• maximize reliability
• minimize number of reactions
• minimize gene regulation
Constraints:
• Stoichiometric equations: Av = b (vj = flux of reaction j )
• Flux bounds: L v U
• Logical: conditional inclusion/exclusion
Mixed Integer Programming Model
optimize cv + dx : Av=b, Ljxj v Ujxj, xj {0, 1}
xj = 0 reaction j suppressed
inhibit pathway P: jP j xj 1
Turn off one member of pathway
(can choose, by some criteria)
Extends to include multiple gene regulation, with arbitrary
logical conditions to determine forced expressions and inhibitions.
Frontiers
Better models
– Scope (depth; breadth)
– Flexibility (manipulate structures, parameters)
– Features (fragility, uncertainty)
Better algorithms
– Scalability (parallel)
– Robustness
– Greater complexity & size
Analysis support
– Visualization
– Structural analysis
– Simplification