* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Macroeconomics Review 2
Exchange rate wikipedia , lookup
Pensions crisis wikipedia , lookup
Steady-state economy wikipedia , lookup
Fear of floating wikipedia , lookup
Interest rate wikipedia , lookup
Early 1980s recession wikipedia , lookup
Full employment wikipedia , lookup
Post–World War II economic expansion wikipedia , lookup
Fei–Ranis model of economic growth wikipedia , lookup
Rostow's stages of growth wikipedia , lookup
Phillips curve wikipedia , lookup
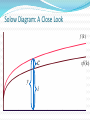
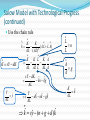
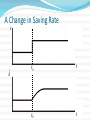
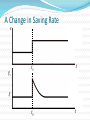
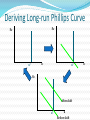
08金融 梁剑雄 Tel:15013229729 QQ:424143870 E-mail: [email protected] Outline Economic Growth (II) Aggregate Supply Review on Solow Model without Technological Progress 1) Production function 1 Y K L Total Per capita yk (0 1) 2) Two-sector economy, and exogenous saving rate Y C I C S , S sY (0 s 1) 3) Given depreciation rate d and constant growth rate of labor n L / L 4) Capital Accumulation Equation Total K sY dK Per capita k sy (n d )k Review on Solow Model without Technological Progress: Steady State Equilibrium Break-even investment Investment per labor y (n d )k f (k ) * sf (k ) Actual investment k * k Solow Diagram: A Close Look f (k ) c y i sf (k ) Solow Diagram: A Close Look Break-even investment Investment per labor y (n d )k f (k ) * c * sf (k ) Actual investment k i k1 k * * k Solow Model: Comparative Statics Investment per labor (n d )k f (k ) ** y* y s ' f (k ) sf (k ) A permanent increase in saving rate k * k ** Adjustment Dynamic Process Adjustment Dynamic Process i * i' ** Investment per capita i i' i* t0 t1 time Consider an economy with only depreciation but without population growth and it’s at the steady state. Now suppose there’s a one-time jump in the numbers of workers. y' k' Consider an economy with only depreciation but without population growth and it’s at the steady state. Now suppose there’s a one-time jump in the numbers of workers. *The Golden Rule The steady-state (per capita) consumption is the distance of steady-state equilibrium (per capita) output and equilibrium (per capita) investment/ saving (n d )k y f (k ) * c k * * sf (k ) k *The Golden Rule (continued) For different saving rate s∈(0,1), steady- state (per capita) investment are all on line (n+d)k (n d )k f (k ) s6 f (k ) s5 f (k ) s4 f (k ) s3 f (k ) s2 f (k ) s1 f (k ) k *The Golden Rule (continued) Steady-state consumptions are shown in the graph (n d )k f (k ) * 3 c * 1 c c * 2 k *The Golden Rule (continued) Here we have the maximal per capita consumption f (k ) c * max k *Solve Golden Rule Consumption in Our C-D Production Function Steady state consumption * c f ( k ) ( n d ) k ( k ) ( n d )k * Solve * * dc* * 1 ( k ) (n d ) 0 * dk Golden-rule capital stock k ** ( nd ) * 1 1 1 s Compare with k * ( )1 nd So optimal saving rate s )1 And the maximal consumption is c** (1 )( ** nd Solow Model with Technological Progress Now think of a C-D production function with labor-augmenting technical progress : Y F ( K , AL) K ( AL)1 (0 1) where A might stand for “knowledge” or the “effectiveness of labor”. REMEMBER: K, A, L are functions of time t. Other assumptions are the same as Solow basic model. In addition, A g A rather than holding A constant (and equal to 1) all the time. Solow Model with Technological Progress (continued) Capital stock per unit of effective labor K ˆ k AL Output per unit of effective labor Y K ( AL)1 K ˆ yˆ ( ) k AL AL AL Solow Model with Technological Progress (continued) Use the chain rule K K ˆ k ( A L L A) 2 AL ( AL) K sY dK K K L K A AL AL L AL A sY dK ˆ ˆ kn kg AL Y yˆ AL Y s dkˆ nkˆ gkˆ AL L n L kˆ syˆ (n g d )kˆ A g A K kˆ AL Solow Model with Technological Progress (continued) Break-even investment Investment per unit of effective labor ŷ (n g d )kˆ f ( kˆ) * sf (kˆ) Actual investment k̂ * k̂ Solow Model with Technological Progress (continued) kˆ skˆ (n g d )kˆ 0 1 s kˆ* ( )1 , n g d Akˆ k kˆ 0 kˆ Ayˆ y yˆ 0 yˆ s yˆ * ( )1 n g d k A kˆ g k A kˆ y A yˆ g y A yˆ K k L gn K k L Y y L gn Y y L A Change in Saving Rate s t t0 k̂ O t0 t A Change in Saving Rate s t0 t t0 t k̂ A Change in Saving Rate s gy t0 t t0 t g A Change in Saving Rate s ln y t0 t t0 t Solow Model: Summary 1) There exist steady states. 2) In the Solow model without technological progress, saving rate and population growth are determinants of per capita income. An increase in saving rate or a decrease in population growth causes a period of growth (but eventually the growth ceases as the new steady state is reached) and increases the long run (steady-state) per capita income. Solow Model: Summary 3) In the Solow model with technological progress, the growth rate of per capita income is determined solely by the exogenous rate of technological rate. 4) Convergence exists, but it’s conditional. 5) A change in the saving rate or in the population growth rate has a level effect but not a growth effect. 6) In the Solow model only changes in the rate of technological progress have growth effects; all other changes have only level effects. Exercise: Solow Model with Technological Progress Suppose that the economy’s production function is Y K AL and that the saving rate ( s) is equal to 16% and that the rate of depreciation ( ) is equal to 10%. Further, suppose that the number of workers grows at 2% per year and that the rate of technological progress is 4% per year. 1) Find the steady state values of The capital stock per effective worker. Output per effective worker. The growth rate of output per effective worker. The growth rate of output per worker. The growth rate of output. Exercise: Solow Model with Technological Progress Suppose that the economy’s production function is Y K AL and that the saving rate ( s) is equal to 16% and that the rate of depreciation ( ) is equal to 10%. Further, suppose that the number of workers grows at 2% per year and that the rate of technological progress is 4% per year. 2) Suppose that the rate of technological progress doubles to 8% per year. Recompute the answers to 1). Explain. 3) Now suppose that the rate of technological progress is still equal to 4% per year, but the number of workers now grows at 6% per year. Recompute the answers to 1). Are people better off in 1) or in 3)? Explain. Keys: kˆ* ( s n g s yˆ * n g )2 1) 2) 3) 1 0.64 0.64 1 0.8 0.8 0 0 0 4% 8% 4% 6% 10% 10% yˆ 0 yˆ y yˆ gg y yˆ Y yˆ gn gn Y yˆ New Growth Theory Introduction to aK model Production function Y aK where Y is output, K is the capital stock, and a is a constant measuring the amount of output produced for each unit of capital. Y K Per capita form a L L y ak New Growth theory L K K L sY dK K L k sy (n d )k 2 L L L L y=ak y sy (n+d)k k0 k In this model, per capita growth can now occur in the long run even without exogenous technological change. Behind the aK Model Diminishing marginal product of capital in microeconomics One important way is to reinterpret K in aK model. -- Knowledge and Human Capital Externalities Endogenous Growth: An Exercise Suppose an economy with a saving rate s 0.1 , a depreciation rate 0.05 . The production function is Y K ( AL) 1/3 2/3 where L 1 . 1) Suppose A is exogenous (and equals 1), compute the steady state of capital stock and GDP. What’s the growth rate of the economy at steady state? 2) Now assume that A is endogenous and it changes when the capital stock changes (for simplicity, just let A K ). In this case, do you think the steady state of capital and GDP exists? What’s the growth rate of the economy? 3) Explain why there’s a difference between the growth rates in 1) and 2). Key to 1) Y K 1/3 L2/3 y k 1/3 sk 1/3 (n )k 0 where s=0.1, n=0, =0.05 s K k ( )3/2 2 2 * * Y * K *1/3 2 Y y 0 Y y Key to 2) Not exist! Y K K sY K sK K ( s ) K Y K s 0.05 Y K A Two-sector Model A sector is C-D production function and the other is AK production function development trap y y=y1+y2 sy (n+d)k y y2 y1 k kA kB k Population Growth Depending on Income Suppose population growth rate is endogenous, and it becomes lower as the income becomes higher. development trap unstable equilibrium (n+d)k HIGH sy sy LOW k0 k* k1 k1 k* k0 (n+d)k Growth Policy: How to get rid of growth trap and obtain long run growth? sy (n+d)k y Big push BIG PUSH kA kB k Growth Policy: How to get rid of growth trap and obtain long run growth? sy 1 y sy (n+d)k sy Big push Raise the saving rate Control the population growth Allocating the investment optimally kA kB k Growth Accounting Generally, we divide the growth in output into three different sources: Increases in capital; Increases in labor; Advances in technology Growth Accounting Suppose the production function is Y AF ( K , L) where A is Total Factor Productivity (TFP) ln Y ln AF ( K , L) Y 1 Y 1 Y 1 Y K L A Y Y K Y L Y A Growth Accounting Y 1 Y 1 Y 1 Y K L A Y Y K Y L Y A 1 Y 1 1 F ( K , L) Y A AF ( K , L) A Y 1 1 A MPK K MPL L Y Y Y A Y MPK K K MPL L L A ( ) ( ) Y Y K Y L A Growth Accounting: Interpretation Y MPK K K MPL L L A ( ) ( ) Y Y K Y L A In a competitive economy, factors are paid their marginal products. MPL L So total payment to labor is MPL L , labor share is Y Total payment to capital is MPK K , capital share is If F ( K , L) is constant return to scale, we can prove ( Thus technological progress, or changes in TFP MPK K Y MPK K MPL L )( ) 1 Y Y Y K L A (1 ) Y K L A 1 is labor share and is capital share Growth Accounting: C-D function Y K L A (1 ) Y K L A 1 is labor share and is capital share If the form of production function is Y AK L1 (0 1) It’s easy to derive that labor share and Y K L A (1 ) Y K L A technological progress, or changes in TFP Growth Accounting: C-D function 1 Y K L A (1 ) Y K L A is labor share and is capital share A Y K L (1 ) A Y K L Here we attribute everything left over to changes in TFP. Measured this way, changes in TFP are called the Solow Residual We also have a per capital form Y L K L A ( ) Y L K L A or y k A y k A *Growth Theory: A Difficult Exercise (Optional) Assume that the production function is a capital augmenting Cobb-Douglas function: Y ( AK ) L1 A And assume A grows at the rate of : A / (1 ), y Y / ( A L ), k K / ( A L) Let 1) Show that y k . 2) Use the capital accumulation equation to show that k sy (n d )k 3) Explain the steady-state of the economy. 4) Compute the steady-state growth rate of y Y L The Long-run AS Curve Y3 Output Y2 Y1 Y0 t0 P t1 AS1 AS2 AS3 Y0 Y1 Y2 t2 Time t3 AS4 Y3 Y Short Run Aggregate Supply P P AS AS Y Y Unemployment: Introduction Labor force, employment, unemployment Full employment Frictional unemployment: the unemployment that exists when the economy is at full employment. ( frictional unemployment rate= natural unemployment rate) Cyclical unemployment is unemployment in excess of frictional unemployment: It occurs when output is below its full-employment level. Natural Rate of Unemployment Natural Rate of Unemployment: A Simple Model (a discrete case) Symbols: Number of labor force Lt Number of employed workers Et Number of unemployed workers U t Unemployment rate ut Assumptions: 1) Labor force has a constant growth rate n , i.e. Lt Lt 1 (1 n) 2) In each period, a constant fraction of employed men lose their job. The proportion is e . 3) In each period, there are also some unemployed men finding their new job. The proportion is b . 4) | 1 b e | 1 1 n Natural Rate of Unemployment: A Simple Model (a discrete case) (continued) Now let’s figure out the recursion. At time t , the unemployed men consists of these two disjoint kind of people: 1) The unemployed men who have not found their jobs (1 b)U t 1 2) Those who were employed last period but lose their jobs this period eEt 1 e( Lt 1 U t 1 ) . Thus, u U t (1 b)U t 1 e( Lt 1 U t 1 ) (1 b e)U t 1 eLt 1 t Lt Lt 1 (1 n) Lt (1 b e)U t 1 eLt 1 Lt 1 (1 n) Lt 1 (1 n) (1 b e) e ut 1 (1 n) (1 n) 1 b e e ut ut 1 1 n 1 n Natural Rate of Unemployment: A Simple Model (a discrete case) (continued) 1 b e e ut ut 1 1 n 1 n According to our assumption | 1 b e | 1 1 n ut is convergent. Let u* lim ut , then t 1 b e * e u u 1 n 1 n * Thereby, gW e u nbe * This is natural rate of unemployment, which is independent of wage. u* u Phillips Curve gw (u u*) Phillips Curve with Expected Inflation Phillips Curve with Expected Inflation People care about real wage rather than nominal wage. w real wage grealwage g w g p p The equation of Phillips grealwage gw e gW curve becomes g w (u u*) e NEW g w (u u*) e If the expectation is u* e OLD t 1 adaptive expectation, then Thus the Phillips curve is g w t 1 (u u*) u Deriving Long-run Phillips Curve gW gW u u* u* gW After shift u* u Before shift u Translation: from Phillips Curve to Short-run AS Curve We want to find a relationship between price level and output: gw (u u*) gp Y Y * First Step: from Wage to Price Level 1) The production function Y L 2) The (nominal) wage is W . W d ( L) dTC d (WL) W dY W MC dY dY dY dY Unit labor cost 3) a) In a competitive market, p MC b) If the competition is imperfect, MR p (1 1 d MR MC p ) p (1 z )W W 1 W 1 1/ d So we have ,where z is a markup. Now we can translate wage to price level: g p gW Second Step: Okun’s Law Okun’s Law Y Y * (u u*) Y* where 2 Note: We have found two relationship of three important variables output, inflation rate and unemployment. They are Phillips curve and Okun’s law. In addition, now introduce the concept of sacrifice ratio: the percentage of output lost for each 1 point reduction in the inflation rate. Final Step: Translation e g (u u*) 1) Phillips curve w 2) g p gW Y Y * (u u*) 3) Okun’s law Therefore Y* * gP ( Y Y ) * Y e Pt Pt 1 g Let * , P , we have P Y t 1 Pt Pt 1 (1 e ) Pt 1 (Y Y *) or Pt Pt Pt 1 (Y Y *) e Summary in AS Curve We derive short run AS curve by translating. 1) The natural rate of unemployment u * 2) The Phillips curve gw (u u*) e g (u u*) 3) The Phillips curve with expected inflation w 4) The long-run Phillips curve u u *. e P P (1 ) Pt 1 (Y Y *) 5) The AS curve t t 1 or Pt Pt e Pt 1 (Y Y *) 6) Adaptive expectation and rational expectation Summary in AS Curve The short-run and long-run AS curve P AS Y* Y Application: Supply Shock Oil price shock P Y* Y Application: Supply Shock A favorable supply shock P Y* Y Application: Supply Shock A favorable supply shock: technological improvements P P Y* Case 1 Y** Y Y* Y** Case 2 Y Exercise: Solow Model and Unemployment Consider how unemployment would affect the Solow growth model. Suppose that output is produced according to the production function Y K [(1 u) L]1, where K is capital, L is the labor force, and u is the natural rate of unemployment. The national saving rate is s , the labor force grows at rate n , and capital depreciates at rate d . 1) Express output per worker (y Y / L) as a function of capital per worker (k K / L) and the natural rate of unemployment. Describe the steady state of this economy. 2) Suppose that some change in government policy reduces the natural rate of unemployment. Describe how this change affects output both immediately and over time. Is the steadystate effect on output larger or smaller than the immediate effect? Explain. Key to 1) 1 y (1 u ) k 1 k sy (n d )k s (1 u ) 1 1 s k (1 u )( ) nd s 1 * y (1 u )( ) nd * k (n d )k Key to 2) (n d )k y (u2* ) y* (u2* ) y (u1* ) sy (u2* ) y1 (u2* ) y * (u1* ) sy (u1* ) k * (u1* ) k * (u2* ) k Key to 2) (Continued) y1 (u2* ) Reference 王志伟译著,Rudiger Dornbusch, Stanley Fischer and Richard Startz, Macroeconomics , Tenth Edition (东 北财经大学出版社,2008) N. Gregory Mankiw, Macroeconomics, Fifth Edition (Worth Publishers,2003) David Romer, Advanced Macroeconomics, Second Edition (McGraw-Hill, 2001) 徐现祥编著,图解宏观经济学,第一版(中国人民大学出 版社,2008) 方福前等译,罗杰·E.A法默(Roger E.A. Farmer)著, 宏观经济学,第二版(北京大学出版社,2009) Olivier Blanchard,Macroeconomics, Second Edition (Prentice Hall,2000)