Download Macroeconomics Review 2

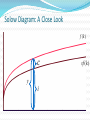
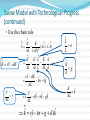
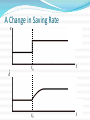
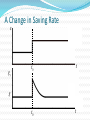
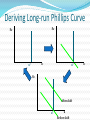
08金融 梁剑雄
Tel：15013229729
QQ：424143870
E-mail： [email protected]
Outline
Economic Growth (II)
Aggregate Supply
Review on Solow Model without
Technological Progress
 1) Production function
 1
Y

K
L
Total
Per capita
yk

(0    1)
 2) Two-sector economy, and exogenous saving rate
Y  C  I  C  S , S  sY (0  s  1)
 3) Given depreciation rate d and constant growth rate

of labor n  L / L
 4) Capital Accumulation Equation

Total K  sY  dK

Per capita k  sy  (n  d )k
Review on Solow Model without Technological
Progress: Steady State Equilibrium
Break-even investment
Investment per
labor
y
(n  d )k
f (k )
*
sf (k )
Actual investment
k
*
k
Solow Diagram: A Close Look
f (k )
c
y
i
sf (k )
Solow Diagram: A Close Look
Break-even investment
Investment per
labor
y
(n  d )k
f (k )
*
c
*
sf (k )

Actual investment
k
i
k1
k
*
*
k
Solow Model: Comparative Statics
Investment per
labor
(n  d )k
f (k )
**
y*
y
s ' f (k )
sf (k )
A permanent
increase in
saving rate
k
*
k
**
Adjustment Dynamic Process
Adjustment Dynamic Process
i
*
i'
**
Investment
per capita
i
i'
i*
t0
t1
time
Consider an economy with only depreciation but
without population growth and it’s at the steady state.
Now suppose there’s a one-time jump in the numbers of
workers.
y'
k'
Consider an economy with only depreciation but
without population growth and it’s at the steady state.
Now suppose there’s a one-time jump in the numbers of
workers.
*The Golden Rule
The steady-state (per capita) consumption is the distance of
steady-state equilibrium (per capita) output and equilibrium (per
capita) investment/ saving
(n  d )k
y
f (k )
*
c
k
*
*
sf (k )
k
*The Golden Rule (continued)
For different saving rate s∈(0,1), steady- state
(per capita) investment are all on line (n+d)k
(n  d )k
f (k )
s6 f (k )
s5 f (k )
s4 f (k )
s3 f (k )
s2 f (k )
s1 f (k )
k
*The Golden Rule (continued)
Steady-state consumptions are shown in the graph
(n  d )k
f (k )
*
3
c
*
1
c
c
*
2
k
*The Golden Rule (continued)
Here we have the maximal
per capita consumption
f (k )
c
*
max
k
*Solve Golden Rule Consumption in Our C-D
Production Function
 Steady state consumption
* 
c  f ( k )  ( n  d ) k  ( k )  ( n  d )k
*
 Solve
*
*
dc*
*  1


(
k
)  (n  d )  0
*
dk
 Golden-rule capital stock k **  (

nd
)
*
1
1
1
s
Compare with k *  (
)1
nd
So optimal saving rate s  


)1
And the maximal consumption is c**  (1   )(
**
nd
Solow Model with Technological
Progress
 Now think of a C-D production function with
labor-augmenting technical progress :
Y  F ( K , AL)  K  ( AL)1 (0    1)
where A might stand for “knowledge” or the “effectiveness
of labor”.
REMEMBER: K, A, L are functions of time t.
 Other assumptions are the same as Solow basic model.

In addition,
A
g
A
rather than holding A constant (and equal to 1) all the time.
Solow Model with Technological
Progress (continued)
 Capital stock per unit of effective labor
K
ˆ
k
AL
 Output per unit of effective labor
Y
K  ( AL)1
K  ˆ
yˆ 

( ) k
AL
AL
AL
Solow Model with Technological Progress
(continued)
 Use the chain rule





K
K
ˆ
k

( A L  L A)
2
AL ( AL)


K  sY  dK


K
K L K A



AL AL L AL A
sY  dK ˆ
ˆ

 kn  kg
AL
Y
 yˆ
AL
Y
s
 dkˆ  nkˆ  gkˆ
AL

L
n
L
 kˆ  syˆ  (n  g  d )kˆ

A
g
A
K
 kˆ
AL
Solow Model with Technological Progress
(continued)
Break-even investment
Investment per unit
of effective labor
ŷ
(n  g  d )kˆ
f ( kˆ)
*
sf (kˆ)
Actual investment
k̂
*
k̂
Solow Model with Technological Progress
(continued)

kˆ  skˆ  (n  g  d )kˆ  0
1
s
kˆ*  (
)1 ,
n g d

Akˆ  k
kˆ
0
kˆ

Ayˆ  y
yˆ
0
yˆ


s
yˆ *  (
)1
n g d


k A kˆ
   g
k A kˆ



y A yˆ
   g
y A yˆ



K k L
   gn
K k L



Y y L
   gn
Y y L
A Change in Saving Rate
s

t
t0
k̂
O
t0
t
A Change in Saving Rate
s
t0
t
t0
t
k̂
A Change in Saving Rate
s
gy
t0
t
t0
t
g
A Change in Saving Rate
s
ln y
t0
t
t0
t
Solow Model: Summary
 1) There exist steady states.
 2) In the Solow model without technological progress,
saving rate and population growth are determinants of
per capita income. An increase in saving rate or a
decrease in population growth causes a period of
growth (but eventually the growth ceases as the new
steady state is reached) and increases the long run
(steady-state) per capita income.
Solow Model: Summary
 3) In the Solow model with technological progress,
the growth rate of per capita income is determined
solely by the exogenous rate of technological rate.
 4) Convergence exists, but it’s conditional.
 5) A change in the saving rate or in the population
growth rate has a level effect but not a growth effect.
 6) In the Solow model only changes in the rate of
technological progress have growth effects; all other
changes have only level effects.
Exercise: Solow Model with Technological Progress
 Suppose that the economy’s production function is
Y  K AL
and that the saving rate ( s) is equal to 16% and that the rate of
depreciation ( ) is equal to 10%. Further, suppose that the
number of workers grows at 2% per year and that the rate of
technological progress is 4% per year.
 1) Find the steady state values of

The capital stock per effective worker.

Output per effective worker.

The growth rate of output per effective worker.

The growth rate of output per worker.

The growth rate of output.
Exercise: Solow Model with Technological Progress
 Suppose that the economy’s production function is
Y  K AL
and that the saving rate ( s) is equal to 16% and that the rate of
depreciation ( ) is equal to 10%. Further, suppose that the
number of workers grows at 2% per year and that the rate of
technological progress is 4% per year.
 2) Suppose that the rate of technological progress doubles
to 8% per year. Recompute the answers to 1). Explain.
 3) Now suppose that the rate of technological progress is
still equal to 4% per year, but the number of workers now
grows at 6% per year. Recompute the answers to 1). Are
people better off in 1) or in 3)? Explain.
Keys:
kˆ*  (
s
n   g
s
yˆ * 
n   g
)2
1)
2)
3)
1
0.64
0.64
1
0.8
0.8
0
0
0
4%
8%
4%
6%
10%
10%

yˆ
0
yˆ


y yˆ
 gg
y yˆ


Y yˆ
 gn gn
Y yˆ
New Growth Theory
 Introduction to aK model
 Production function
Y  aK
where Y is output, K is the capital stock, and a is a constant
measuring the amount of output produced for each unit of
capital.
Y
K
 Per capita form
a
L
L
 y  ak
New Growth theory



L K  K L sY  dK K L
k


 sy  (n  d )k
2
L
L
L L

y=ak
y
sy
（n+d）k
k0
k
In this model, per capita growth can now occur in the long run even
without exogenous technological change.
Behind the aK Model
 Diminishing marginal product of capital in
microeconomics
 One important way is to reinterpret K in aK model.
-- Knowledge and Human Capital  Externalities
Endogenous Growth: An Exercise
 Suppose an economy with a saving rate s  0.1 , a
depreciation rate   0.05 . The production function is
Y  K ( AL)
1/3
2/3
where L  1 .
 1) Suppose A is exogenous (and equals 1), compute the
steady state of capital stock and GDP. What’s the growth
rate of the economy at steady state?
 2) Now assume that A is endogenous and it changes when
the capital stock changes (for simplicity, just let A  K ).
In this case, do you think the steady state of capital and
GDP exists? What’s the growth rate of the economy?
 3) Explain why there’s a difference between the growth
rates in 1) and 2).
Key to 1)
Y  K 1/3 L2/3
y  k 1/3
sk 1/3  (n   )k  0 where s=0.1, n=0,  =0.05
s
K  k  ( )3/2  2 2
*
*

Y *  K *1/3  2


Y y
 0
Y y
Key to 2)
Not exist!
Y K

K  sY   K  sK   K  ( s   ) K


Y K
  s    0.05
Y K
A Two-sector Model
 A sector is C-D production function and the other is
AK production function
development trap
y
y=y1+y2
sy
（n+d）k
y
y2
y1
k
kA
kB
k
Population Growth Depending on Income
 Suppose population growth rate is endogenous, and it
becomes lower as the income becomes higher.
development trap
unstable equilibrium
（n+d）k
HIGH sy
sy
LOW
k0
k*
k1
k1
k*
k0
(n+d)k
Growth Policy:
How to get rid of growth
trap and obtain long run growth?
sy
（n+d）k
y
 Big push
BIG PUSH
kA
kB
k
Growth Policy:
How to get rid of growth
trap and obtain long run growth?
sy
1
y
sy
（n+d）k
sy
 Big push
 Raise the saving rate
 Control the population growth
 Allocating the investment optimally
kA
kB
k
Growth Accounting
 Generally, we divide the growth in output into three
different sources:

Increases in capital;
 Increases in labor;
 Advances in technology
Growth Accounting
 Suppose the production function is
Y  AF ( K , L)
where A is Total Factor Productivity (TFP)
ln Y  ln AF ( K , L)

Y 1 Y  1 Y  1 Y 

K
L
A
Y Y K
Y L
Y A
Growth Accounting

Y 1 Y  1 Y  1 Y 

K
L
A
Y Y K
Y L
Y A

1 Y
1
1

F ( K , L) 
Y A AF ( K , L)
A



Y 1
1
A
 MPK K  MPL L
Y Y
Y
A




Y
MPK  K K MPL  L L A
(
) (
) 
Y
Y
K
Y
L A
Growth Accounting: Interpretation




Y
MPK  K K MPL  L L A
(
) (
) 
Y
Y
K
Y
L A
 In a competitive economy, factors are paid their marginal
products.
MPL  L
 So total payment to labor is MPL  L , labor share is
Y
 Total payment to capital is MPK  K , capital share is
 If F ( K , L) is constant return to scale, we can prove
(
 Thus
technological progress,
or changes in TFP
MPK  K
Y
MPK  K
MPL  L
)(
) 1
Y
Y




Y
K
L A
   (1   ) 
Y
K
L A
1

is labor share and
is capital share
Growth Accounting: C-D function




Y
K
L A
   (1   ) 
Y
K
L A
1

is labor share and
is capital share
 If the form of production function is
Y  AK  L1 (0    1)
 It’s easy to derive that labor share   
and




Y
K
L A
   (1   ) 
Y
K
L A
technological progress,
or changes in TFP
Growth Accounting: C-D function




1
Y
K
L A
   (1   ) 
Y
K
L A




is labor share and
is capital share

A Y
K
L
    (1   )
A Y
K
L
Here we attribute everything left over to changes in
TFP. Measured this way, changes in TFP are called
the Solow Residual
 We also have a per capital form





Y L
K L A
 (  )
Y L
K L A
 or



y
k A
 
y
k A
*Growth Theory: A Difficult Exercise (Optional)
 Assume that the production function is a capital
augmenting Cobb-Douglas function:

Y  ( AK ) L1
A

 And assume A grows at the rate of  :
A





/
(1


),
y

Y
/
(
A
L
),
k

K
/
(
A
L)
 Let
 1) Show that y  k  .
 2) Use the capital accumulation equation to show that

k  sy  (n    d )k
 3) Explain the steady-state of the economy.
 4) Compute the steady-state growth rate of y 
Y
L
The Long-run AS Curve
Y3
Output
Y2
Y1
Y0
t0
P
t1
AS1 AS2 AS3
Y0 Y1 Y2
t2
Time
t3
AS4
Y3
Y
Short Run Aggregate Supply
P
P
AS
AS
Y
Y
Unemployment: Introduction
 Labor force, employment, unemployment
 Full employment
 Frictional unemployment: the unemployment that exists
when the economy is at full employment.
 ( frictional unemployment rate= natural unemployment rate)
 Cyclical unemployment is unemployment in excess of
frictional unemployment: It occurs when output is
below its full-employment level.
Natural Rate of Unemployment
Natural Rate of Unemployment:
A Simple Model (a discrete case)
 Symbols:
 Number of labor force Lt
 Number of employed workers Et
 Number of unemployed workers U t
 Unemployment rate ut
 Assumptions:
 1) Labor force has a constant growth rate n , i.e. Lt  Lt 1 (1  n)
 2) In each period, a constant fraction of employed men
lose their job. The proportion is e .
 3) In each period, there are also some unemployed men
finding their new job. The proportion is b .
 4) | 1  b  e | 1
1 n
Natural Rate of Unemployment:
A Simple Model (a discrete case) (continued)
 Now let’s figure out the recursion.
 At time t , the unemployed men consists of these two disjoint
kind of people:
 1) The unemployed men who have not found their jobs (1  b)U t 1
 2) Those who were employed last period but lose their jobs this
period eEt 1  e( Lt 1  U t 1 ) .
 Thus, u  U t  (1  b)U t 1  e( Lt 1  U t 1 )  (1  b  e)U t 1  eLt 1
t

Lt
Lt 1 (1  n)
Lt
(1  b  e)U t 1
eLt 1

Lt 1 (1  n)
Lt 1 (1  n)

(1  b  e)
e
ut 1 
(1  n)
(1  n)
1 b  e
e
ut 
ut 1 
1 n
1 n
Natural Rate of Unemployment:
A Simple Model (a discrete case) (continued)
1 b  e
e
ut 
ut 1 
1 n
1 n
 According to our assumption
|
1 b  e
| 1
1 n
 ut is convergent. Let u*  lim ut , then
t 
1 b  e *
e
u 
u 
1 n
1 n
*
 Thereby,
gW
e
u 
nbe
*
 This is natural rate of unemployment,
which is independent of wage.
u*
u
Phillips Curve
gw   (u  u*)
Phillips Curve with Expected Inflation
Phillips Curve with Expected Inflation
 People care about real wage rather than nominal wage.
w
real wage   grealwage  g w  g p
p
 The equation of Phillips
 grealwage  gw   e
gW
curve becomes
g w     (u  u*)
e
NEW
 g w     (u  u*)
e
 If the expectation is
u*
e
OLD

  t 1
adaptive expectation, then
 Thus the Phillips curve is g w   t 1   (u  u*)
u
Deriving Long-run Phillips Curve
gW
gW
u
u*
u*
gW
After shift
u*
u
Before shift
u
Translation: from Phillips Curve to
Short-run AS Curve
 We want to find a relationship between price level and
output:
gw   (u  u*)
gp
Y Y *
First Step: from Wage to Price Level
 1) The production function Y   L
 2) The (nominal) wage is W .
W
d (  L)
dTC d (WL)
W dY W

MC 




dY
dY
dY
 dY  Unit labor cost
 3) a) In a competitive market, p  MC 
b) If the competition is imperfect,
MR  p (1 
1
d
MR  MC  p 
)
p
(1  z )W
W

1
W
1  1/  d 
So we have
,where z is a markup.

 Now we can translate wage to price level: g p  gW
Second Step: Okun’s Law
 Okun’s Law
Y Y *
  (u  u*)
Y*
where   2
 Note: We have found two relationship of three important
variables output, inflation rate and unemployment. They
are Phillips curve and Okun’s law.
 In addition, now introduce the concept of sacrifice ratio:
the percentage of output lost for each 1 point reduction
in the inflation rate.
Final Step: Translation
e
g


  (u  u*)
 1) Phillips curve w
 2) g p  gW
Y Y *
  (u  u*)
 3) Okun’s law
 Therefore
Y*

*
gP   
(
Y

Y
)
*
Y
e
Pt  Pt 1

g

 Let   * , P
, we have
P
Y
t 1
Pt  Pt 1 (1   e )  Pt 1 (Y  Y *)
 or
Pt  Pt  Pt 1 (Y  Y *)
e
Summary in AS Curve
 We derive short run AS curve by translating.
 1) The natural rate of unemployment u *
 2) The Phillips curve gw   (u  u*)
e
g


  (u  u*)
 3) The Phillips curve with expected inflation w
 4) The long-run Phillips curve u  u *.
e
P

P
(1


)  Pt 1 (Y  Y *)
 5) The AS curve t t 1
or
Pt  Pt e  Pt 1 (Y  Y *)
 6) Adaptive expectation and rational expectation
Summary in AS Curve
 The short-run and long-run AS curve
P
AS
Y*
Y
Application: Supply Shock
 Oil price shock
P
Y*
Y
Application: Supply Shock
 A favorable supply shock
P
Y*
Y
Application: Supply Shock
 A favorable supply shock: technological improvements
P
P
Y*
Case 1
Y**
Y
Y* Y**
Case 2
Y
Exercise: Solow Model and Unemployment
 Consider how unemployment would affect the Solow growth
model. Suppose that output is produced according to the
production function Y  K  [(1  u) L]1, where K is capital, L
is the labor force, and u is the natural rate of unemployment.
The national saving rate is s , the labor force grows at rate n ,
and capital depreciates at rate d .
 1) Express output per worker (y  Y / L) as a function of capital
per worker (k  K / L) and the natural rate of unemployment.
Describe the steady state of this economy.
 2) Suppose that some change in government policy reduces
the natural rate of unemployment. Describe how this change
affects output both immediately and over time. Is the steadystate effect on output larger or smaller than the immediate
effect? Explain.
Key to 1)
1
y  (1  u )
k


1
k  sy  (n  d )k  s (1  u )
1
1
s
k  (1  u )(
)
nd

s 1
*
y  (1  u )(
)
nd
*

k  (n  d )k
Key to 2)
(n  d )k
y (u2* )
y* (u2* )
y (u1* )
sy (u2* )
y1 (u2* )
y * (u1* )
sy (u1* )
k * (u1* )
k * (u2* )
k
Key to 2) (Continued)
y1 (u2* )
Reference
 王志伟译著，Rudiger Dornbusch, Stanley Fischer and





Richard Startz, Macroeconomics , Tenth Edition (东
北财经大学出版社,2008)
N. Gregory Mankiw, Macroeconomics, Fifth Edition
(Worth Publishers,2003)
David Romer, Advanced Macroeconomics, Second
Edition (McGraw-Hill, 2001)
徐现祥编著，图解宏观经济学，第一版（中国人民大学出
版社，2008）
方福前等译，罗杰·E.A法默（Roger E.A. Farmer）著，
宏观经济学，第二版（北京大学出版社，2009）
Olivier Blanchard，Macroeconomics， Second Edition
（Prentice Hall，2000）