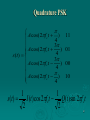Download 05-SignalEncodingTechniques

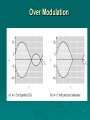
Data and Computer
Communications
Chapter 5 – Signal Encoding
Techniques
Eighth Edition
by William Stallings
Lecture slides by Lawrie Brown
Signal Encoding Techniques
Even the natives have difficulty mastering this
peculiar vocabulary
—The Golden Bough, Sir James George Frazer
Encoding Techniques
 Digital
data
• Digital Signal
• Analog Signal
 Analog
data
• Digital Signal
• Analog Signal
3
Signal Encoding Techniques
Digital Data, Digital Signal
 Digital



signal
discrete, discontinuous voltage pulses
each pulse is a signal element
binary data encoded into signal elements
Signal Encoding Techniques
 Modulation:

The process of encoding source data onto a carrier
signal with frequency f
 Carrier

signal
A continuous constant-frequency that is chosen to
be compatible with the transmission media.
 Baseband

signal (modulating signal)
The input signal (analog or digital)
 The
result of modulating the carrier signal is
called the modulated signal s(t)
Some Terms
 Unipolar

All signal elements have the same sign.
 Polar

One logic state represented by positive voltage
the other by negative voltage.
 data

rate
Rate of data transmission in bits per second
Some Terms
 duration

or length of a bit
Time taken for a transmitter to emit the bit
(1/R)
 modulation


Rate at which the signal level changes.
Measured in baud = signal elements per
second.
 mark

rate
and space
Binary 1 and Binary 0 respectively
Interpreting Signals
 need


to know
timing of bits - when they start and end
signal levels
 factors




affecting signal interpretation
signal to noise ratio
data rate
bandwidth
encoding scheme
Data Encoding Criteria
 An
increase in DR increases BER
 An increase in SNR decreases BER
 An increase in BW allows an increase in
DR
 The other factor that improves
performance is the encoding scheme

The encoding scheme is simply the
mapping from data bits to signal elements
10
Encoding Schemes








Non-return to Zero-Level (NRZ-L)
Non-return to Zero Inverted (NRZI)
Bipolar -AMI
Pseudoternary
Manchester
Differential Manchester
B8ZS
HDB3
11
Comparing Encoding
Schemes

Signal spectrum




With lack of high-frequency components, less
bandwidth required
With no DC component, AC coupling via transformer
possible
Concentrate power in the middle of the bandwidth
Clocking


Ease of determining beginning and end of each bit
position
Not easy task.
• Separate clock for synchronization .(expensive)
• Synchronization based on the transmitted signal
12
Comparing Encoding
Schemes

Error detection


Signal interference and noise immunity


Can be built into signal encoding
Performance in the presence of noise
Cost and complexity


The higher the signal rate to achieve a given data
rate, the greater the cost
Some codes require signal rate greater than data rate
13
Encoding Schemes
Nonreturn to Zero-Level (NRZ-L)

two different voltages for 0 and 1 bits
 voltage constant during bit interval



no transition I.e. no return to zero voltage
such as absence of voltage for zero, constant positive
voltage for one
more often, negative voltage for one value and
positive for the other
Nonreturn to Zero Inverted



nonreturn to zero inverted on ones
constant voltage pulse for duration of bit
data encoded as presence or absence of signal transition at
beginning of bit time



transition (low to high or high to low) denotes binary 1
no transition denotes binary 0
example of differential encoding since have



data represented by changes rather than levels
more reliable detection of transition rather than level
easy to lose sense of polarity
NRZ Pros & Cons
 Pros


easy to engineer
make good use of bandwidth
 Cons


dc component
lack of synchronization capability
 used
for magnetic recording
 not often used for signal transmission
Spectral Density of Various Signal
Encoding Schemes

Most of the energy in NRZ and NRZI signals is between dc and half the bit rate.

Data rate of 9600 bps, most of the energy in the signal is concentrated between dc and 4800 Hz.
RZ encoding
19
Multilevel Binary Bipolar-AMI
 Use
more than two levels
 Bipolar-AMI








zero represented by no line signal
one represented by positive or negative pulse
one pulses alternate in polarity
no loss of sync if a long string of ones
long runs of zeros still a problem
no net dc component
lower bandwidth
easy error detection
Multilevel Binary Bipolar-AMI
Multilevel Binary
Pseudoternary
 one
represented by absence of line signal
 zero represented by alternating positive
and negative
 no advantage or disadvantage over
bipolar-AMI
 each used in some applications
Multilevel Binary
Pseudoternary
Multilevel Binary Issues

synchronization with long runs of 0’s or 1’s



can insert additional bits, cf ISDN
scramble data (later)
not as efficient as NRZ

each signal element only represents one bit
• receiver distinguishes between three levels: +A, -A, 0


a 3 level system could represent log23 = 1.58 bits
requires approx. 3dB more signal power for same
probability of bit error
Theoretical Bit Error Rate for
Various Encoding
Manchester Encoding





has transition in middle of each bit period
transition serves as clock and data
low to high represents one
high to low represents zero
used by IEEE 802.3
Differential Manchester
Encoding

midbit transition is clocking only
 transition at start of bit period representing 0
 no transition at start of bit period representing 1


this is a differential encoding scheme
used by IEEE 802.5
Biphase Pros and Cons

Con




at least one transition per bit time and possibly two
maximum modulation rate is twice NRZ
requires more bandwidth
Pros



synchronization on mid bit transition (self clocking)
has no dc component
has error detection
• Absence of expected transition
• Noise would have to invert both before and after expected
transition.
Modulation Rate
Modulation/Baud Rate

Baud rate, also known as signaling rate or modulation
rate:



Signal elements per second (baud).
The rate at which signal elements are transmitted.
In general,
D = R/L = R/(log2 M)
•
•
•
•

D = modulation rate, baud
R = data rate, bps
M = number of different signal elements = 2L
L = number of bits per signal element
For two-level signaling (binary),
bit rate is equal to the baud rate.
30
Modulation/Baud Rate

Example: a stream of binary ones at 1 Mbps.
NRZI is 1 MBaud.
Manchester has 0.5 bits/signal element:
Baud rate = Bit rate/Nb
= 1 Mbps/0.5
= 2 MBaud
31
Signal element versus data element
32
Scrambling

use scrambling to replace sequences that would
produce constant voltage
 these filling sequences must




produce enough transitions to sync
be recognized by receiver & replaced with original
be same length as original
design goals




have no dc component
have no long sequences of zero level line signal
have no reduction in data rate
give error detection capability
B8ZS

Bipolar With 8 Zeros Substitution
 Based on bipolar-AMI



Causes two violations of AMI code


If octet of all zeros and last voltage pulse preceding
was positive encode as 000+-0-+
If octet of all zeros and last voltage pulse preceding
was negative encode as 000-+0+Unlikely to occur as a result of noise
Receiver detects and interprets as octet of all
zeros
34
B8ZS
V: violation voltage that breaks AMI rule of encoding (opposite
polarity from the previous)
B: Bipolar a nonzero level voltage in accordance with the AMI
rule
35
Scrambling Techniques

HDB3:






High Density Bipolar 3 zeros.
String of four zeros replaced with one or two pulses.
4 zeros are encoded as either 000-, 000+, +00+, or -00Number of the non-zero pulses after last substitution is odd
use (000V)
Number of the non-zero pulses after last substitution is even
use (B00V)
Substitution rule is s.t. the 4th bit is always a code violation,
and successive violations are of alternate polarity (not to
introduce dc component)
36
B8ZS and HDB3
Digital Data, Analog Signal
 main


use is public telephone system
has freq range of 300Hz to 3400Hz
use modem (modulator-demodulator)
 encoding



techniques
Amplitude shift keying (ASK)
Frequency shift keying (FSK)
Phase shift keying (PK)
Modulation Techniques
Amplitude Shift Keying

One binary digit represented by presence of
carrier, at constant amplitude
 Other binary digit represented by absence of
carrier
 A cos( 2f ct )
s(t )  
0

binary 1
binary 0
where the carrier signal is A cos(2πfct)
ASK Characteristics
 Susceptible
to sudden gain changes
 Inefficient modulation technique
 used for


On voice-grade lines, used up to 1200 bps
Used to transmit digital data over optical fiber
41
ASK Implementation
42
Amplitude Shift Keying
The carrier is only one simple sine wave, the process of
modulation produce s a nonperiodic composite signal
43
Binary Frequency-Shift Keying
(BFSK)

Two binary digits represented by two different frequencies
near the carrier frequency

 A cos2f1t 
s t   

 A cos2f 2t 

binary 1
binary 0
where f1 and f2 are offset from carrier frequency fc by equal but
opposite amounts
44
BFSK Characteristics
 Less
susceptible to error than ASK
 On voice-grade lines, used up to 1200bps
 Used for high-frequency (3 to 30 MHz)
radio transmission
 Can be used at higher frequencies on
LANs that use coaxial cable
45
Relationship between baud rate and
bandwidth in FSK
46
FSK on Voice Grade Line
47
Multiple FSK
 each
signalling element represents more
than one bit
 more than two frequencies used
 more bandwidth efficient
 more susceptible to error
Multiple FSK
si (t )  A cos 2f i t ,
 fi = fc




1 i  M
+ (2i – 1 – M) fd
fc = the carrier frequency
fd = the difference frequency
M = number of different signal element = 2L
L = number of bits per signal element
49
Multiple FSK

To mach the data rate of the input, each signal element
is hold for a period of Ts = LT


T is a bit period
One signal element encodes L bits

total bandwidth required = 2Mfd
 minimum frequency separation = 2fd = 1/Ts
 modulator requires a bandwidth of Wd = 2Mfd =
M/Ts
50
Multiple FSK
Multiple FSK
Phase Shift Keying

phase of carrier signal is shifted to represent data
 binary PSK

two phases represent two binary digits
 A cos(2f ct )
s(t )  
 A cos(2f ct   )
 A cos( 2f ct )

 A cos(2f ct )
binary 1
binary 0
Phase Shift Keying
 we
define d(t) as the discrete function
 takes on the value of +1 for one bit time if
the corresponding bit in the bit stream is 1
 the value -1 of for one bit time if the
corresponding bit in the bit stream is 0
sd (t )  Ad (t ) cos(2f ct )
Phase Shift Keying
 differential

PSK
phase shifted relative to previous transmission
rather than some reference signal
Quadrature PSK
 get
more efficient use if each signal
element represents more than one bit



eg. shifts of /2 (90o)
each element represents two bits
split input data stream in two & modulate onto
carrier & phase shifted carrier
 can
use 8 phase angles & more than one
amplitude

9600bps modem uses 12 angles, four of
which have two amplitudes
Quadrature PSK

 A cos( 2f c t

 A cos( 2f c t

s (t )  
 A cos( 2f c t


A cos( 2f c t




)
4
3
)

4
3
)

4


4
)
11
01
00
10
1
1
s(t ) 
I (t ) cos 2f ct 
Q(t ) sin 2f ct
2
2
57
Quadrature PSK
58
QPSK and OQPSK
Modulators
Quadrature PSK
60
Performance of Digital to
Analog Modulation Schemes

Bandwidth

depends on a variety of factors
• including the definition of bandwidth used
• The filtering technique used to create the bandpass signal

ASK/PSK bandwidth directly relates to bit rate
BT  (1  r ) R

R = bit rate

r = related to techniques by which the signal is filtered. (0 < r
< 1)

FSK
BT  2F  (1  r ) R
Performance of Digital to
Analog Modulation Schemes



for MFSK & MPSK have tradeoff between
bandwidth efficiency and error performance
MPSK
MFSK
 1 r
1 r 
BT  
 R  
 L 
 log 2 M
 (1  r ) M
BT  
 log 2 M

 R


 R

Performance of Digital to
Analog Modulation Schemes
 in


presence of noise:
bit error rate of PSK and QPSK are about 3dB
superior to ASK and FSK
for MFSK & MPSK have tradeoff between
bandwidth efficiency and error performance
Quadrature Amplitude
Modulation

QAM used on asymmetric digital subscriber line
(ADSL) and some wireless
 combination of ASK and PSK
 logical extension of QPSK
 send two different signals simultaneously on
same carrier frequency




use two copies of carrier, one shifted 90°
each carrier is ASK modulated
two independent signals over same medium
demodulate and combine for original binary output
QAM Modulator
s(t )  d1 (t ) cos 2f ct  d 2 (t ) sin 2f ct
QAM Variants
 two



each of two streams in one of two states
four state system
essentially QPSK
 four

level ASK
level ASK
combined stream in one of 16 states
 have
64 and 256 state systems
 improved data rate for given bandwidth

but increased potential error rate
QAM
Analog Data, Digital Signal
 digitization
is conversion of analog data
into digital data which can then:



be transmitted using NRZ-L
be transmitted using code other than NRZ-L
be converted to analog signal
 analog
to digital conversion done using a
codec


pulse code modulation
delta modulation
Digitizing Analog Data
Pulse Code Modulation (PCM)
 sampling


“If a signal is sampled at regular intervals at a
rate higher than twice the highest signal
frequency, the samples contain all information
in original signal”
eg. 4000Hz voice data, requires 8000 sample
per sec
 strictly

theorem:
have analog samples
Pulse Amplitude Modulation (PAM)
 so
assign each a digital value
PCM Example
PCM Block Diagram
Quantization Error
 Samples
are quantized:
– Approximations mean it is impossible to
recover original exactly.
– Quantizing error or noise.
– n-bit encoding, there are 2n levels:
Vmin  Vmax

L
L
number of levels
 The error for any sample

-∆/2 ≤ error ≤ ∆/2
74
Quantization Error
 The
contribution of the quantization error to the
SNRdB of a signal depends on L or bits per
sample n
SNR = 20 log2n +1.76 dB = 6.02 n + 1.76 dB
≈ 6n dB.
 each additional bit used for quantizing
increases SNR by about 6 dB, which is a
factor of 4.
Non-Linear Coding
Companding

The same effect can be achieved by using uniform
quantizing but companding (compressingexpanding) the input analog signal
 Companding


compresses the intensity range of a signal by imparting
more gain to weak signals than to strong signals on input
At output, the reverse operation is performed
Companding
Delta Modulation

analog input is approximated by a staircase
function


can move up or down one level () at each sample
interval
has binary behavior



since function only moves up or down at each sample
interval
hence can encode each sample as single bit
1 for up or 0 for down
Delta Modulation

must be chosen to produce a balance
between two types of errors or noise.
 When the analog waveform is changing
very slowly, there will be quantizing noise.
This noise increases as  is increased.
 when the analog waveform is changing
more rapidly than the staircase can follow,
there is slope overload noise
Delta Modulation Example
Delta Modulation Operation
PCM verses Delta Modulation
 DM
has simplicity compared to PCM
 but has worse SNR
 issue of bandwidth used

eg. for good voice reproduction with PCM
• want 128 levels (7 bit) & voice bandwidth 4khz
• need 8000 x 7 = 56kbps
 data
compression can improve on this
 still growing demand for digital signals

use of repeaters, TDM, efficient switching
 PCM
preferred to DM for analog signals
Analog Data, Analog Signals

Modulation: combine an input signal m(t)
 with a carrier fc to produce a signal s(t).
 modulate carrier frequency with analog data
 why modulate analog signals?



higher frequency can give more efficient transmission
permits frequency division multiplexing (chapter 8)
types of modulation



Amplitude
Frequency
Phase
Analog
Modulation
Techniques



Amplitude Modulation
Frequency Modulation
Phase Modulation
DSBTC
 AM
is the simplest form of modulation
s(t )  [1  na x(t )] cos 2f ct
 x(t)
: the input signal
 na : known as the modulation index

the ratio of the amplitude of the input signal to
the carrier
Example
DSBTC

The envelope of the resulting signal is [ 1 + na x(t) ]
 If na < 1, the envelope is an exact reproduction of
the original signal
 If na > 1, the envelope will cross the time axis and
information is lost
Envelopes for various values of m
90
Over Modulation
91
DSBTC Spectrum

The spectrum consists of the original carrier plus
the spectrum of the input signal translated to
 na should be as large as possible

most of the signal power is used to carry information

n2

a
P  P 1 
t
c
2






SSB
 SSB
take advantage of the fact that each
side band contains all the transmitted
information
 BW is half, BT = B
 Less power is required, (no transmission of
the other side band)
93
Angle Modulation

FM and PM are special cases of angle
modulation
s(t )  Ac cos[2f ct   (t )]

For phase modulation

PM
 (t )  n p m(t )

For frequency modulation, the derivative of the
phase is proportional to the modulating signal

FM
 (t )  n f m(t )
'
94
Angle modulation

In PM the instantaneous phase deviation is
proportional to m(t)
 For FM

Frequency can be defined as the rate of change of
phase of a signal, the inst. Frequency of s(t) is
d
2f i (t )  [2f c t   (t )]
dt
1 '
f i (t )  f c 
 (t )
2
95
Angle modulation

The peak deviation in FM can be seen to be

an increase in the magnitude of m(t) will increase
delta F

should increase the transmitted bandwidth

But will not increase the average power level of
the FM signal
 Compare with AM

level of modulation affects the power in the AM signal
but does not affect its bandwidth.
96
Angle modulation

AM is linear process and produces frequencies
that are the sum and difference of the carrier
signal and the components of the modulating
signal

For AM

Angle modulation is not linear which includes
cos(phi).
 It may contain an infinite BW
97
Angle Modulation

For practical, Carson’s rule
BT  2(   1) B
where
n p Am


   F n f Am


2B
 B

For FM
for PM 


for FM 

BT  2F  2 B
98
Summary
 looked




at signal encoding techniques
digital data, digital signal
analog data, digital signal
digital data, analog signal
analog data, analog signal