* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download E E 2315 Circuits I Lecture 9
Current source wikipedia , lookup
Stray voltage wikipedia , lookup
Ringing artifacts wikipedia , lookup
Resonant inductive coupling wikipedia , lookup
Mains electricity wikipedia , lookup
Alternating current wikipedia , lookup
Voltage optimisation wikipedia , lookup
Switched-mode power supply wikipedia , lookup
Resistive opto-isolator wikipedia , lookup
Surge protector wikipedia , lookup
Opto-isolator wikipedia , lookup
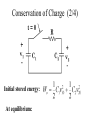
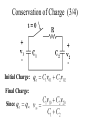
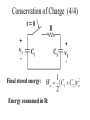
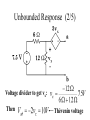
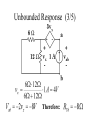
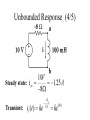
E E 2315 Lecture 10 Natural and Step Responses of RL and RC Circuits Conservation of Charge (1/4) • Energy transferred if v10 v20 • Total system charge is conserved Conservation of Charge (2/4) Initial stored energy: At equilibrium: Conservation of Charge (3/4) Initial Charge: Final Charge: Since Conservation of Charge (4/4) Final stored energy: Energy consumed in R: Conservation of Flux Linkage (1/3) • Energy transferred if i10 i20 • Total system flux linkage is conserved. Initial stored energy: At equilibrium: Conservation of Flux Linkage (2/3) Initial flux linkage: Final flux linkage: Since Conservation of Flux Linkage (3/3) Final stored energy: Energy consumed in R: Natural RL Response (1/2) • Inductor has initial current, io. • Switch opens at t = 0 • Inductor current can’t change instantaneously Natural RL Response (2/2) Integrate: KVL: Separate the variables: Exponential of both sides: Natural RC Response (1/2) • Capacitor has initial voltage, vo. • Switch closes at t = 0. • Capacitor voltage can’t change instantaneously KCL: Separate the variables: Natural RC Response (2/2) Integrate: Exponential of both sides: RL Step Response (1/4) • Make-before-break switch changes from position a to b at t = 0. • For t < 0, Io circulates unchanged through inductor. RL Step Response (2/4) • For t > 0, circuit is as below. • Initial value of inductor current, i, is Io. • The KVL equation provides the differential equation. RL Step Response (3/4) Solution has two parts: Steady State Response Transient Response Determine k by initial conditions: RL Step Response (4/4) • Inductor behaves as a short circuit to DC in steady state mode RC Step Response (1/3) • Switch closes at t = 0. • Capacitor has initial voltage, Vo. v-i relationship: By KVL & Ohm’s Law: RC Step Response (2/3) • Response has two parts – steady state – transient • Use initial voltage to determine transient Steady State Response Transient Response RC Step Response (3/3) • Capacitor becomes an open circuit to DC after the transient response has decayed. Unbounded Response (1/5) • Need Thévenin equivalent circuit from terminal pair connected to inductor • Let initial current = 0A in this example. Unbounded Response (2/5) Voltage divider to get vx: Then Thévenin voltage Unbounded Response (3/5) Therefore: Unbounded Response (4/5) Steady state: Transient: Unbounded Response (5/5) Use initial conditions to determine k. Complete response is unbounded: