* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Document
Opto-isolator wikipedia , lookup
Non-radiative dielectric waveguide wikipedia , lookup
Rechargeable battery wikipedia , lookup
Energy storage wikipedia , lookup
Surface-mount technology wikipedia , lookup
Capacitor types wikipedia , lookup
Supercapacitor wikipedia , lookup
Electrolytic capacitor wikipedia , lookup
Tantalum capacitor wikipedia , lookup
Aluminum electrolytic capacitor wikipedia , lookup
Niobium capacitor wikipedia , lookup
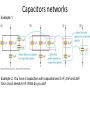
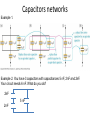
EXAM 1, September 22, Thursday Ch.21-23, Lectures 1-6. 1. Finding E(x,y,z) or E(r) using N kq kQ r i a) E of a point charge E 2 r0 and Etotal 2 0i r i i 1 superposition principle, r Qencl qencl E dA E b) or Gauss’s law 0 0 A surface c) or E i Ex j E y k Ez Ex V V V , Ey , Ez x y z 2. Finding a force a)FQq qEQ N b) or F kQi r0i q total i 1 ri 3. Finding potential using a) V V E dl kq b) or potential of a point charge V (r ) r N and superposition principle Vtotal (r ) kQi i 1 r i 4) Finding the work and potential energy b a b a q E dl q(Va Vb ) U a U b U b Wab a Preparation for Exam 1. Look in advance at the formula sheet on the website of the course 2. Problems worked out in Lecture notes 3. Previous midterm exams on my website 4. WebCT and assigned homework At the Exam • You’ll get 3 problems+ formula sheet • Ask me the questions if you do not understand the formulation of the problem • Start with the figure • Get a general (algebraic) solution • Indicate the units • Get numerical results if required (bring your calculator) Lectures 7 (Ch. 24) Capacitance and capacitors 1. Definitions and functions 2. Types of capacitors 3. Effective capacitance (capacitors in series and parallel) 4. Dielectrics 5. Energy stored in capacitor Capacitor is a device to store the charge and energy. It consists of two conductors (+Q,-Q), separated by a dielectric. Store Q and V in order 1. To use it on demand (camera flash, energy back up,…) 2. To block surges of Q and V protecting sensitive devices 3. Part of tuner of a radio, selecting specific frequency of radio waves 4. Binary code of a memory Q does not depend neither on Q no on V. Capacitance: C V It is defined by the geometrical sizes and by a dielctric inside Types of capacitors 1. II plate capacitor Q C ; V Ed ; V Q E 0 A 0 A 0 Qd V ;C A 0 d Spherical capacitor Q C ; Vab Vab E dr ; b a b a b kQ kQ 1 1 ba E 2 r0 ; Vab 2 dr kQ( ) kQ( ) r a b ab a r 40 ab 0 A C ba d A 4a 2 4b 2 4ab; d b a Cylindrical capacitor b Q C ; Vab E dr ; Vab a a b b 2 k 2k b E r0 ; Vab dr 2k ln r r a a 20 L Q ;C b L ln a In the case d a, b ( where d b a ) b d d ln ln( 1 ) a a a 0 A C ; A 2aL d SI unit of C [C]=[Q]/[V]=1C/1V=1F(farad) Symbol: Typically C~1pF-1 F d 1mm A=? Michael Faradey (1791-1867) ! Supercapacitors: C~1F-1kF 1. Using porous conductors (carbon) to increase an effective A EL 2. Electrolyte (EL) as 1 of 2 conductors oxide layer with an effective d~1nm d EL EL Commercial capacitors Capacitors in parallel: C=C1+C2 Q Q1 Q2 C C1 C2 V V Capacitors in series: 1 1 1 C C1 C2 1 V V1 V2 1 1 C Q Q C1 C2 Capacitors networks Example 1. Example 2. You have 3 capacitors with capacitances 5 nF, 2nF and 2nF. Your circuit needs 6 nF. What do you do? Capacitors networks Example 1. Example 2. You have 3 capacitors with capacitances 5 nF, 2nF and 2nF. Your circuit needs 6 nF. What do you do? 2nF 5 nF 2nF Dielectrics different from vacuum or air are typically used in capacitors • to increase the capacitance: C=KC0, K>1 • to improve a mechanical stability (avoid touching between conducting plates) • to increase the dielectric strength compared to air (for air: Ecr=3MV/m) Polarization of dielectric in E Suppose capacitor was charged, σ is the surface charge density, E0 0 Then a battery was removed and a dielectric was inserted. Polarization of dielectric led to induced charge on the plates,σi, reducing E between plates: i E i i 1 E ; 1 1 0 E0 K K≥1 is a dielectric constant, ε=Kε0 is a dielectric permittivity E0 V0 E ; V Ed V ; K K 0 K i 1 1 1 i (1 ) K K A 0 K A Q Q C K C0 K V V0 d d Suppose capacitor is connected to a battery with voltage, V. Then a dielectric is inserted. Q0 Q Q V C0 C KC0 v Q KQ0 ; Q Q0 Q0 ( K 1) Qi 1 1 1 Qi Q(1 ) Q Q0 Q K K Battery sup plies an additional ch arg e to compensate for Qi and to keepV const V 0K 0 E const d 0K 0 ! For charges interacting in a dielectric medium Coulomb’s Law 1 Qq Fe r 2 o 4 r Qencl E dA Gauss’s Law Q q Potentical energy stored in the capacitor q dW dqV , V C V dq Q E -q q q Q2 U W dq C 2C 0 2 2 Q CV QV Q CV ; U 2C 2 2 Density of Energy 2 2 2 U CV AE d U E u Volume Ad 2 Ad d 2 Ad 2 2 U can be viewed as energy stored in E inside capacitor Insert dielectric, C=KC0 2 2 Q CV QV U 2C 2 2 Does U ↑or↓? 1. Charged Capacitor. Battery is removed. Then a dielectric is inserted. Q -Q + - F - dl F + 2 2 U0 Q Q Q const ; U U0 2C 2 KC0 K 2 2 V0 KC0V0 U0 CV or V ; U U0 2 K 2 2K K final U 0 U W Fel dl 0 0 2. Capacitor is connected to battery with V=const. Then a dielectric is inserted 2 2 KC0V CV V const ; U KU 0 U 0 2 2 or Q KQ0 (Q VC VC0 K Q0 K ) 2 V 2 2 K Q0 Q U KU 0 U 0 2C 2 KC0 Energy is supplied by the battery, increasing the charge on the plates and keeping V=const Find 1)Charge and energy of the 1st capacitor before the switch was closed. 2) Charge of each capacitor, voltage and total energy after closing the switch . Q0V0 0.058 J 2 Q Q1 Q Q Q 1 1 V 1 2 0 Q1 ( ) 0 C1 C2 C2 C1 C1 C2 Q0 V0C1 960C ; U initial Q1 Q0C1 2 Q0 640C C1 C2 3 Q2 Q0C2 1 Q0 320C C1 C2 3 Q1V Q2V Q0V Q0 V 80V ;U final 0.038 J C1 C2 2 2 2 Example 24.15 Data: C1= C2 = C3 = C4 =C=4ϻF; Vab =28V , , , Find: Q1 Q2 , Q3,Q4 V1 V2 , V3,V4 C12 C / 2, C123 3C / 2, 1 C1234 1 1 3C 12F , C1234 2.4F C123 C4 5 5 Q4 28VX 2.4F 67.2C ; Q4 67.2C V4 16.8V C4 4F V3 28V 16.8V 11.2V , Q3 11.2VX 4F 44.8C V3 V1 V2 5.6V 2 Q1 Q2 5.6VX 4F 22.4C