Download CH06 Steady state Analysis

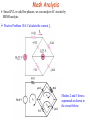
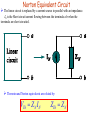
Chapter 6(b)
Sinusoidal Steady State Analysis
Chapter Objectives:
 Apply previously learn circuit techniques to sinusoidal steady-state
analysis.
 Learn how to apply nodal and mesh analysis in the frequency domain.
 Learn how to apply:
 superposition,
 Source Transformation
 Thevenin’s and Norton’s theorems
in the frequency domain.
Steps to Analyze AC Circuits

Transform the circuit to the Phasor Domain.

Solve the problem using circuit techniques listed below
1)
2)
3)
4)
5)

*Nodal Analysis
*Mesh Analysis
Superposition
Source transformation
*Thevenin or Norton Equivalents
Transform the resulting circuit back to time domain.
Steps to Analyze AC Circuits
 Transform the circuit to the phasor or frequency
domain.
 Solve the problem using circuit techniques (nodal
analysis, mesh analysis, superposition, etc.).
 Transform the resulting phasor to the time domain.
Time to Freq
Solve
Variables in Freq
Freq to Time
Nodal Analysis






Since KCL is valid for phasors, we can analyze AC circuits by
NODAL analysis.
Determine the number of nodes within the network.
Pick a reference node and label each remaining node with a
subscripted value of voltage: V1, V2 and so on.
Apply Kirchhoff’s current law at each node except the reference.
Assume that all unknown currents leave the node for each
application of Kirhhoff’s current law.
Solve the resulting equations for the nodal voltages.
For dependent current sources: Treat each dependent current
source like an independent source when Kirchhoff’s current law
is applied to each defined node. However, once the equations are
established, substitute the equation for the controlling quantity to
ensure that the unknowns are limited solely to the chosen nodal
voltages.
Nodal Analysis
 Since KCL is valid for phasors, we can analyze AC circuits by
NODAL analysis.
 Practice Problem 10.1: Find v1 and v2 using nodal analysis
Nodal Analysis
 Practice Problem 10.1
Nodal Analysis
 Practice Problem 10.1
Mesh Analysis
 Since KVL is valid for phasors, we can analyze AC circuits by
MESH analysis.
 Practice Problem 10.4: Calculate the current Io
Meshes 2 and 3 form a
supermesh as shown in
the circuit below.
Mesh Analysis
 Practice Problem 10.4: Calculate the current Io
Mesh Analysis
 Practice Problem 10.4: Calculate the current Io
Superposition Theorem
The superposition theorem eliminates the need for solving simultaneous linear
equations by considering the effect on each source independently.
 To consider the effects of each source we remove the remaining sources; by
setting the voltage sources to zero (short-circuit representation) and current sources
to zero (open-circuit representation).
 The current through, or voltage across, a portion of the network produced by
each source is then added algebraically to find the total solution for current or
voltage.
 The only variation in applying the superposition theorem to AC networks with
independent sources is that we will be working with impedances and phasors
instead of just resistors and real numbers.
 The superposition theorem is not applicable to power effects in AC networks
since we are still dealing with a nonlinear relationship.
 It can be applied to networks with sources of different frequencies only if the
total response for each frequency is found independently and the results are
expanded in a nonsinusoidal expression .
 One of the most frequent applications of the superposition theorem is to
electronic systems in which the DC and AC analyses are treated separately and the
total solution is the sum of the two.
Superposition Theorem
When a circuit has sources operating at different
frequencies,
• The separate phasor circuit for each frequency
must be solved independently, and
• The total response is the sum of time-domain
responses of all the individual phasor circuits.
Superposition Theorem
 Superposition Theorem applies to AC circuits as well.
 For sources having different frequencies, the total response must be obtained by
adding individual responses in time domain.
Exp. 10.6 Superposition Technique for sources having different frequencies
a) All sources except DC 5-V set to zero
b) All sources except 10cos(10t) set to zero
Superposition Theorem
Exp. 10.6 Superposition Technique for sources having different frequencies
c) All sources except 2 sin 5t set to zero
vo= v1+ v2+ v3
Superposition Theorem
Superposition Theorem
Superposition Theorem
P.P.10.6 Superposition Technique for sources having different Frequencies
Superposition Theorem
Superposition Theorem
Source Transformation
 Transform a voltage source in series with an impedance to a current source in
parallel with an impedance for simplification or vice versa.
Source Transformation
 Practice Problem 10.4: Calculate the current Io
If we transform the current source to a voltage source, we obtain the circuit shown in Fig. (a).
Source Transformation
 Practice Problem 10.4: Calculate the current Io
Thevenin Equivalent Circuit
 Thévenin’s theorem, as stated for sinusoidal AC circuits, is changed only to
include the term impedance instead of resistance.
 Any two-terminal linear ac network can be replaced with an equivalent
circuit consisting of a voltage source and an impedance in series.
 VTh is the Open circuit voltage between the terminals a-b.
 ZTh is the impedance seen from the terminals when the independent sources are
set to zero.
Norton Equivalent Circuit
 The linear circuit is replaced by a current source in parallel with an impedance.
IN is the Short circuit current flowing between the terminals a-b when the
terminals are short circuited.
 Thevenin and Norton equivalents are related by:
VTh  Z N I N
ZTh  Z N
Thevenin Equivalent Circuit
P.P.10.8 Thevenin Equivalent At terminals a-b
Thevenin Equivalent Circuit
P.P.10.9 Thevenin and Norton Equivalent
for Circuits with Dependent Sources
To find Vth , consider the circuit in Fig. (a).
Thevenin Equivalent Circuit
P.P.10.9 Thevenin and Norton Equivalent for Circuits with Dependent Sources
Thevenin Equivalent Circuit
P.P.10.9 Thevenin and Norton Equivalent for Circuits with Dependent Sources
Thevenin Equivalent Circuit
P.P.10.9 Thevenin and Norton Equivalent for Circuits with Dependent Sources
Since there is a dependent source, we can find the impedance by inserting a voltage source
and calculating the current supplied by the source from the terminals a-b.