* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Computer interfacing Introduction
Electrical substation wikipedia , lookup
Electric power system wikipedia , lookup
Current source wikipedia , lookup
Signal-flow graph wikipedia , lookup
Three-phase electric power wikipedia , lookup
Spectral density wikipedia , lookup
Power engineering wikipedia , lookup
History of electric power transmission wikipedia , lookup
Dynamic range compression wikipedia , lookup
Utility frequency wikipedia , lookup
Public address system wikipedia , lookup
Stray voltage wikipedia , lookup
Power inverter wikipedia , lookup
Negative feedback wikipedia , lookup
Scattering parameters wikipedia , lookup
Variable-frequency drive wikipedia , lookup
Pulse-width modulation wikipedia , lookup
Voltage regulator wikipedia , lookup
Voltage optimisation wikipedia , lookup
Resistive opto-isolator wikipedia , lookup
Audio power wikipedia , lookup
Schmitt trigger wikipedia , lookup
Power electronics wikipedia , lookup
Buck converter wikipedia , lookup
Alternating current wikipedia , lookup
Regenerative circuit wikipedia , lookup
Mains electricity wikipedia , lookup
Switched-mode power supply wikipedia , lookup
Week 1
CENG4480_A1
Op Amps and Analog Interfacing
Analog interfacing techniques
op-amps (v.5f)
1
Computer interfacing
Introduction
To learn how to connect the computer to various
physical devices.
Some diagrams of this manuscript are taken from
the following references:
[1] S.E. Derenzo, Interfacing -- A laboratory approach
using the microcomputer for instrumentation, data
analysis and control prentice hall.
[2] D.A. Protopapas, Microcomputer hardware design,
Prentice hall
[3] G C Loveday, Designing electronic hardware,
Addison Wesley
op-amps (v.5f)
2
Topics include:
Overall interfacing schemes
Analog interface circuits, active filters
Analog/digital conversions
sensors, controllers
Control techniques
Advanced examples
op-amps (v.5f)
3
Overall view: a typical data
acquisition and control system
Timer
Digital control
circuit
Sensor
Op-amp
Mechanical
device
filter
Sample
&
Hold
Power
circuit
op-amps (v.5f)
A/D
Computer
D/A
4
Analog interface example1
Audio recording systems
Audio recording systems
Audio signal is 20~20KHz
Sampling at 40KHz, 16-bit is Hi-Fi
Stereo ADC requires to sample at 80KHz.
Calculate storage requirement for one hour?
Audio recording standards
Audio CD
Mini-disk MD
MP3
op-amps (v.5f)
5
Analog interface example2
Surround sound audio systems
A common two channels audio CD
Calculate storage size for one hour of recording
of a CD. 44.1KHz*2bytes*60sec*60min*2 channels=633.6Mbytes
Calculate the play time of a CD.
700M/(2bytes*44.1KHz*2channels*60sec)=61.4 minutes
6 Channels: Front R/L,Rear R/L, Middle,
Sub woofer
44.1KHz,
Calculate the sampling frequency.
op-amps (v.5f)
6
Analog interface example3
Play stations and Wii
Play station 3, Analog hand held
controller
(http://ryangenno.tripod.com/images/PlayStat
ion3-system.gif)
Wii,
http://www.onlinekosten.de/news/bilder/wii_
controller.jpg
Driving wheel
http://www.bizrate.com/gamecontrollers/logit
ech-driving-force-driving-force-wheel-pid11297651/
op-amps (v.5f)
7
Operational Amplifier choices (op
amp)
Why use op amp?
What kinds of inputs/outputs do you want?
What frequency responses do you want?
op-amps (v.5f)
8
Biasing
{Biasing in electronics is the method of
establishing predetermined voltages or
currents at various points of an electronic
circuit for the purpose of establishing
proper operating conditions in electronic
components}, from
https://en.wikipedia.org/wiki/Biasing
op-amps (v.5f)
9
Direct Current (DC) amplifier
Example: use power op amp (or transistor) to control the
DC motor operation.
Need to maintain the output voltage at a certain level for a
long time.
All DC (biased) levels must be designed accurately .
Circuit design is more difficult.
DC
Op-
Load:
Source
amp
DC
motor
op-amps (v.5f)
10
Alternating Current (AC) amplifier
Example: Microphone
amplifier, signal is AC and is
changing at a certain
frequency range. Current is
AC
OpLoad
alternating not stable.
Source
amp
Use capacitors to connect
different stages, so no need
Each stage can have its owe
to consider biasing problems.
biasing level. A capacitor is
an isolator, so the circuit is
Biased at
easier to be designed.
Vcc
Vcc/2=2.5V
Biased at
Vcc/2
op-amps (v.5f)
11
Factors for choosing an amplifier
Source DC or AC ?
DC-direct current amplifier
DC(static or slow changing
input, without decoupling
capacitors)
AC(for fast changing input,
use decoupling capacitors)
Input range, biased : absolute
min, max voltage
Output range, biased : absolute
min, max voltage
Frequency: range, allowed
attenuation in dB
Noise tolerance
Power – output current/output
impedance.
DC
Op-
Source
amp
Load
AC-alternating current
amplifier
AC
Op-
Source
amp
op-amps (v.5f)
Load
12
op-amps (v.5f)
Input impedance (Rin) and
Output impedance (Rout)
Why do we prefer High Rin and Low Rout?
Because it is more efficient.
Stage1(sensor)
Vout1
Rout1
Is
equivalent Vout1
to
Stage 2
Vin2 Rin2
Rout1
Rin2
Vin2=
Vout1*Rin2/(Rout1+Rin2)
To maximize Vin2 (input voltage driving stage 2)
We make Rout1 lower, Rin2 higher.
Good choice: Rin1M or over, Rin 10
13
Sensor
Vout_sen Rout_sen
1mV
Student ID: __________________
Name: ______________________
Vout_ Date:_______________
amp (Submit this at the end of the
lecture.)
x1000
Rin_amp
Exercise 1.1
Sensor (Rout_sen) Vout_sen=1mV is sent to an
amplifier with Rin_amp, gain 1000
a) Rout_sen =10 , Rin_amp=1M, calculate the
output voltage (out_amp) of the amplifier
b) Rout_sen =2K , Rin_amp=10K, calculate the
output voltage of the amplifier
c) Which above scheme would you prefer and why?
op-amps (v.5f)
14
Meaning of power gain in dB
(Decibel)
Vout=output
Vin=input
Voltage gain =Vout/Vin
Power gain =(Vout)2/ (Vin)2
Power gain in dB=10*log10(Power gain )
=20* Log10|(Vout/Vin)|=20*Log10|G|,
where G= Voltage gain
When power gain=(Vout/Vin)2=1, voltage_gain=1,
power_gain is 0dB
When power gain=(Vout/Vin)2=0.5,
voltage_gain=(0.5)1/2=0.707, power_gain is -3dB
op-amps (v.5f)
15
op-amps (v.5f)
Frequency-gain plot
When power gain=(Vout/Vin)2=1, voltage_gain=1, power_gain is 0dB
When power gain=(Vout/Vin)2=0.5, voltage_gain=(0.5)1/2=0.707,
power_gain is -3dB
An amplifier frequency-gain is important to understand its
chartered at different frequencies.
Horizontal axis is frequency (log scale) in Hz,
Vertical axis is gain in dB Gain is 0dB
Gain is -3dB
Power gain is 0.5
Power gain is 1
0dB
-3dB
Power
Gain (dB)
Log
Frequency
One decade = one number is 10 times of the other number
Slope:
20
dB/decade
drop
16
Exercise 1.2: General concept
about OP amps
Controllable gain
For DC or AC amplifier
Not too high frequency responses
K=Gain * bandwidth =gain_bandwidth_product
Calculate K at A,B,C. Gain=power gain
At A, GainA=________,(BA)=_______,KA=___
At B, GainB=________,(BB)=_______,KB=___
At C, GainC=________,(BC)=_______,KC=___
What is your conclusion based
on the above calculation?
op-amps (v.5f)
B
A
C
Power gain in dB=
10*log10(Power gain )
17
Week 2
Operational amplifiers (op-amps)
ideal op-amps
inverting amplifier
non-inverting amplifier
voltage follower
current-to-voltage amplifier
summing amplifier
full-wave rectifier
instrumental amplifier
op-amps (v.5f)
18
Ideal Vs. realistic
op-amp
Ideal
A= infinite
Zin= infinite
2
Realistic Rin
105->108
106(bipolar input)
1012(FET input)
output offset exists
V-
_
LM741
V+
+
6
V0=A(V+-V-)
3
op-amps (v.5f)
19
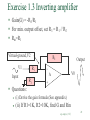
Exercise 1.3 Inverting amplifier
Gain(G) = -R2/R1
For min. output offset, set R3 = R1 // R2
Rin=R1
Virtual-ground,V2
V1
Input
R2
R1
Output
_
V0
A
R3
+
Questions:
(i) Derive the gain formula (See appendix)
(ii) If R1=1K, R2=10K, find G and Rin
op-amps (v.5f)
20
Exercise 1.4 Non-inverting amplifier
Voltage Gain(G) 1 + (R2/R1)
For min. offset output , set R1//R2=Rsource
High input resistance
V1
Input
+
A
V0
_
R2
V2
Questions:
Output
R1
(i) Derive the gain formula (See appendix)
(ii) If R1=1K, R2=10K, find G and Rin
op-amps (v.5f)
21
Differential amplifier
V0=(R2/R1)(V2-V1)
Minimum output offset R1 //R2 =R3 //R4
R2
V1
Input
_
R1
A
V2
+
R3
V0
Output
R4
Exercise: proof the gain formula
op-amps (v.5f)
22
Exercise 1.5
A temperature sensor has an offset of 100mV (produces
an output of 100mV at 0 °C-degrees Celsius), and the
gradient is 10 mV per °C. The temperature to be
measured is ranging from 0 to 50 °C.
The required ADC input range is 0 to 9Volts.
Given that the power supply is +/-9V, design a
differential amplifier for this application.
op-amps (v.5f)
23
Voltage follower (Unit voltage gain,
high current gain, high input impedance)
Gain=1,
Rin=high
For minimum output offset R=Rsource
V1
+
A
V0=V1
_
R
Exercise: proof the gain formula
op-amps (v.5f)
24
Current to voltage converter:
Application to photo detector – no loading
effect for the light detector
V0=I R
I should not be too large otherwise offset
voltage will be too high.
Photodiode
Light
detector I
R
_
A
V0
+
See http://hyperphysics.phy-astr.gsu.edu/hbase/electronic/photdet.html#c1
Exercise: proof the formula
op-amps (v.5f)
25
Summing amplifier
V0 = -{(V1/R1)+(V2/R2)+(V3/R3)}R
V1
R1
V2
R2
V3
R3
I1
R
_
V0
I1+I2+I3
+
Output
Inputs
Exercise: proof the gain formula
op-amps (v.5f)
26
Exercise 1.6
Discuss what kind of amplifiers should we use
for the following sensors?
Condenser microphone(+/-10mV)
Audio amplifier from MP3 player to speaker
Ultrasonic sensors (+/-1mV) to ADC (analog to
digital converter) (0-5V)
Accelerometers (+/-5V), or (+/-500mV)
Temperature sensors to ADC (010mv)
Moving coil microphone with 50Hz noise (+/0.5mV)
op-amps (v.5f)
27
Integrator
Ref
http://www.physics.ucdavis.edu/classes/Physics116/Physics116A04F.html
Reading exercise: http://www.electronics-tutorials.ws/opamp/opamp_6.html
op-amps (v.5f)
28
Differentiator
Ref
http://www.physics.ucdavis.edu/classes/Physics116/Physics116A04F.html
Reading exercise: http://www.electronics-tutorials.ws/opamp/opamp_7.html
op-amps (v.5f)
29
Op-amp characteristics
Input and output offset voltages
It is affected by power supply variations,
temperature, and unequal resistance paths.
Some op-amps have offset setting inputs.
Unequal resistance paths and bias currents on
inverting and non-inverting inputs
Temperature variations -- read data sheet
for operating temperatures
op-amps (v.5f)
30
Op-amp dynamic response
Slew rate -- the maximum rate of output
change (V/us) for a large input step change.
A741 slew rate=0.5V/ s. Fast slew rate is
important in video circuits , fast data
acquisition etc.
Gain bandwidth product
higher gain --> lower frequency response
lower gain --> higher frequency response
op-amps (v.5f)
31
Common mode gain
If the two inputs (V+,V-) are connected together
and is given Vc, output is found to be Vo.
ideal differential amplifier only amplifies the voltage
difference between its two inputs, so Vo should be 0.
But in practice it is not.
This deficiency can be measured by the
Common_mode_gain=Gc=Vo/Vc.
op-amps (v.5f)
32
Diagram of gain bandwidth product, from [1]
op-amps (v.5f)
Hz
33
Instrumental amplifier
To make a better DC amplifier from op-amps
Applications: Digital Oscilloscope DSO input amplifiers,
amplifiers in medical measurement systems
op-amps (v.5f)
Diagram of instrumental amplifier, from [1]
34
Instrumental amplifier
It has all the advantages of an amplifier.
Gain(G)=V0/(V+-V-)
=(R4/R3)[1+(2R2/R1)] (typically 10 to 1000)
Even V+=V-= Vc , there is a slight output because
of the Common Mode Gain=Gc=V0/Vc
Therefore, V0= G(V+-V-)+GcVc
To measure this imperfection, Common Mode
rejection ratio (CMRR)=G/Gc (typically 103 to
107, or 60 to 140 dB)is used , the bigger the better.
op-amps (v.5f)
35
Comparing amplifiers, from [1]
High Rin
Op Inv. Noninv. Diff. Instu.
Amp Amp Amp Amp Amp
Yes No Yes No Yes
Diff’tial Yes
input
No
No
Yes
Yes
Defined No
gain
Yes
Yes
Yes
Yes
op-amps (v.5f)
36
Operational amplifier selection
techniques and keywords
National semiconductor is the main manufacturer: See
http://www.national.com/appinfo/milaero/analog/highp.html
General Purpose: LM741*
High Slew Rate:50V/ ms --> 2000V/ ms (how fast the output can be changed)
Follower (high speed):50MHz
Low Supply Current: 1.5mA --> 20 µA/Amp
Low offset voltage: 100 µV
Low Noise
Low Input Bias Current: 50pA -->10pA
High Power : 0.2A --> 2A
Low Drift: 2.5 mV/ _C --> 1.0 mV/ _C
Dual/Quad
High Power Bandwidth High Power Bandwidth : 300KHz - 230Mhz
op-amps (v.5f)
37
Practical op-amp usage examples
Example 1: Working with one power supply
Example 2: Active filters
Example 3: Sample and hold
Example 4: Example 4: Voltage
Comparator and schmit trigger input ciruit
Example 5: Power amplifier
op-amps (v.5f)
38
Example 1: Single power supply
for op-amps
Small systems usually have a single power
supply
Output V0 is biased at E/2 rather than 0.
E.g. Inverting amplifier. Gain-R2/R1 E=10V
R2
E/2=5V
V1
E
E/2=5V
V+
A
VVo
+
0-Volt
_
R1
R3
0Volt
R=20K
E/2=5V
R=20K
E Volts Power supply
op-amps (v.5f)
39
Typical A.C. amplifier design
Condenser a microphone amplifier circuit, and the diagram showing the output
swing around the biased (steady state volateg) 2.5V. The capacitors isolate the
stages of different biases. Condenser MIC output impedance is 75 Ohms. What is
the input impedance of the amplifier? Answer: See previous notes on inverting
amplifier
5V
Biased
at
around
4V
Biased
at
around
2.5V
Biased at
around 2.5V
2.5V
Output to Mic-in of
power amplifier
2.5V
op-amps (v.5f)
40
Example 2: Active filters
(analog and using op-amps)
Applications: accept or reject certain signals
with specific frequencies. High-pass, lowpass, band-pass etc. E.g.
reject noise
extract signal after demodulation
reject unwanted side effect signals
op-amps (v.5f)
41
Types
2-1: Low pass
2-2: High pass
2-3: Band stop (notch): e.g. noise removal
2-4: Band pass
Week 3
op-amps (v.5f)
42
Recall: definition of power gain in
decibel (dB)
Output power is P2, input power is P1
Power Gain in dB=10 log10 (P2/P1)
Or, output voltage is V2, input voltage is V1
Assume load R is the same, power=V2/R
Power Gain in dB=10 log10 (V22/ V12)
Power Gain in dB=20 log10 |(V1/ V2)|
=20 log10 |G|, where G=voltage gain
op-amps (v.5f)
43
Time domain vs. frequency
domain
Time domain: we talk about voltage gain
against time
Time domain signal plot
+1V
Voltage
Vpp=Peak-to-Peak voltage
0
Time :(Seconds, usually linear scale)
-1V
Frequency domain: we talk about the
voltage gain against frequency.
Power
Gain (dB)
Frequency domain signal plot
0dB
-3dB
op-amps (v.5f)
Frequency (Hz)
(can use log scale)
44
Important terms for filters: Formulas are
not important, remember the frequencygain curve and concepts
Pass band-- range of frequency that are
passed unfiltered
Stop band -- range of frequency that are
rejected.
Corner frequency -- where amplitude
dropped by (0.5)1/2=0.707
I.e. in dB: 20*log(0.707) = -3dB
Settling time -- time required to rise within
10% of the final value after a step input. 45
op-amps (v.5f)
op-amps (v.5f)
2-1 Low pass
Only low frequency signal can pass
one-pole: attenuates slower 20dB/decade
two-pole: attenuates faster 40dB/decade
Applications:
remove high freq. Noise,
remove high freq. before sampling to avoid
aliasing noise
Reading exercise, please read this webpage:
Ref : http://www.electronics-tutorials.ws/filter/filter_5.html
46
Diagram for low-pass one pole filter, from [1]
for simplicity make R2/R1=1, Gain
G( f )
G(f) in dB
R2 / R1
f
1
fc
2
20 dB/decade
drop
3dB
fc Freq.
Corner frequency fc, f c
Exercise: proof the gain formula basedon the
inverting amplifier gain formula (See appendix) op-amps (v.5f)
1
2R2C
47
Formula
f Frequency. To proof | G |
V0 R2
V1 R1
1
2
, where f c
f
1
fc
X // R2
1
Voltage Gain G c
, by definition X c
R1
j 2fC
1
2R2C
1
R2
j
2
fC
X // R2
j 2fC
G c
R1
1 j 2fC
R1 R2
j 2fC
Put f c
1
2R2C
G
R2
f
R1 1 j
fc
| G |
R2
R1
1
f
1
fc
2
, since
1
1 ja
1
1 a
2
see appendix
op-amps (v.5f)
48
2-1a
Low pass, one pole filter formulas
for simplicity make R2/R1=1K
G( f )
R2 / R1
f
1
fc
2
Corner frequency= fc=1/(2R2C)
The gain drops 6dB/octave or 20 dB/decade
op-amps (v.5f)
49
Exercise 1.7
What is the meaning of -3dB cut off?
What is the meaning of 20dB/decade drop?
Plot the power gain(dB) vs frequency
diagram of, R1=R2=1K , C=1uF
Voltage gain G ( f )
R2 / R1
f
1
fc
op-amps (v.5f)
2
50
Diagram for Low-pass two-pole filter, from [1]
for simplicity make R3/(R2+R1)=1
G( f )
Gain
40 dB/decade
G(f) in dB
drop
R3 /( R2 R1 )
f
1
fc
2
6dB
Where fc=(R1//R2)/2 C1 =(2 R3C2)-1
fc Freq.
op-amps (v.5f)
51
2-1b
Low-pass two-pole filter formulas
for simplicity make R3/(R2+R1)= 1
G( f )
R3 /( R2 R1 )
f
1
fc
2
Corner frequency=fc
fc=(R1//R2)/2 C1 =(2 R3C2)-1 when gain
G drops at -6dB.
G is dropping at 40dB/decade
op-amps (v.5f)
52
Exercise 1.8
What is the meaning of -6dB cut off?
What is the meaning of 40dB/decade drop?
Plot the power gain(dB) vs frequency
diagram of, R1=R2=1K ,R3=2K, C=1uF
Voltage gain G ( f )
R3 /( R2 R1 )
f
1
fc
2
Compare the difference between one-pole
and two-pole low pass filters
op-amps (v.5f)
53
Matlab, lp42.m
%lp42.m, ceg3480 matlab demo %low pass filter-one pole
clear
f=[0:100:2000]
N=length(f)
fc=1000
for i=1:N
% -----gain1 , low pass one pole , for simplicity make (R2/R1)=1
gv1(i)=-1/sqrt(1+(f(i)/fc)^2);
%db=10*log_base10(power1/power2); or dB=20*log_base10(voltage1/voltage2;
gain1_db(i)=20*log10(abs(gv1(i)));
% -----gain2 , low pass two pole , for simplicity make {R3/(R1+R2)}=1
gv2(i)=-1/(1+(f(i)/fc)^2);
%db=10*log_base10(power1/power2); or dB=20*log_base10(voltage1/voltage2;
gain2_db(i)=20*log10(abs(gv2(i)));
end
% %========================================================
figure(1)
clf
limit_y=min(gain2_db)
semilogx(f,gain1_db,'g-.')
hold on
semilogx(f,gain2_db,'b--')
%-----------------------semilogx([fc,fc],[0,limit_y],'k-.')
legend('one pole','two pole','fc=1000',4);
%------------------------------------------------------semilogx(f,ones(N)*-3,'r')
text(f(N),-3,'- 3d B line')
%-----------------------semilogx(f,ones(N)*-6,'r')
text(f(N),-6,'- 6d B line')
ylabel('low pass filter gain in d B')
xlabel('freq Hz f in log scale')
op-amps (v.5f)
54
Plotting the comparison of the low
pass filters (one-pole, two-pole)
20dB/decade
Slope less steep
40dB/decade
Slope more steep
op-amps (v.5f)
55
2-2
High pass
Only high frequency signal can pass
One-pole: attenuates slower 20dB/decade
Two-pole: attenuates faster 40dB/decade
Applications:
Remove low freq. Noise (50Hz main)
Remove DC offset drift.
op-amps (v.5f)
56
2-2a
Diagram for high-pass one-pole filter, from [1]
For simplicity make R1=R2, R3=R2 // R1
G( f )
20 dB/decade
Gain G(f) in dB
drop
f
fc
f
1
fc
1
where f c
2R1C
2
,
fc
op-amps (v.5f)
3dB
Freq.
high freq. Cutoff
unintentionally
Created
by
Op-amp 57
High-pass one-pole filter formulas
G( f )
f
fc
f
1
fc
1
where f c
2R1C
2
,
Corner frequency= fc=1/{2 (R1C)}
At low f , |Glow_freq|=f/fc;
at high f , | Ghigh_freq |=R2/R11
Since op-amp has a certain gain-bandwidth, so at high
frequency the gain drops. So all op-amp high-pass filters
are actually band-pass.
op-amps (v.5f)
58
Matlab hp52.m
%hp52.m ceg3480 matlab demo %high pass filter-one pole
clear
f=[500:100:100000]
N=length(f)
fc=1000
for i=1:N
% -------------------gain3 , high pass ,one pole
gv3(i)=-(f(i)/fc)/sqrt(1+(f(i)/fc)^2);
%db=10*log_base10(power1/power2); or dB=20*log_base10(voltage1/voltage2;
gain3_db(i)=20*log10(abs(gv3(i)));
end
% %========================================================
figure(1)
clf
limit_y=min(gain3_db)
semilogx(f,gain3_db,'k-.')
hold on
%-----------------------semilogx([fc,fc],[0,limit_y],'g-.')
legend('one pole','fc=1000',4);
%------------------------------------------------------semilogx(f,ones(N)*-3,'r')
text(f(N),-3,'- 3d B line')
ylabel('high pass filter gain in d B')
op-amps (v.5f)
xlabel('f freq in log scale')
59
high pass one pole filter
op-amps (v.5f)
60
2-3
Band stop (notch) filter
Suppresses a narrow frequency band of
signal
op-amps (v.5f)
61
2-3
Band pass filter
Passes a frequency band of signal.
op-amps (v.5f)
62
Diagram for Notch filter (band-stop), from [1]
op-amps (v.5f)
63
Notch filter (band-stop) formulas
Rejects a narrow band of frequencies and
passes all others. Say reject the 60Hz main
noise for noise removal. Voltage
Gain in dB
High Q,Fc1=(4 RC)-1
Low Q, Fc2=( RC)-1
frequency
op-amps (v.5f)
64
Example 3: Sample and hold
amplifier
For a fast changing signal, if you want to know the
voltage level of a snap shot (e.g. using a slow AD
converter to view a short pulse), you need a
sample and hold device, e.g. AD582, AD389 etc.
At Sample(S), V0=V1; at Hold(H) the output is
held at the level just before switching to H. It is
like taking a photograph of a signal.
Some AD converter has this circuit incorporated
inside.
op-amps (v.5f)
65
Diagram for Sample and hold amplifier, from [1]
op-amps (v.5f)
Sample: sampling
Hold: When the switch is
at H, Vo keeps unchanged
for a long time. So the
Analog–to-digital
converter ADC can have
more time for data
conversion
Hold
Slight
droop
may
occur
66
Example 4: Voltage Comparator
with hysteresis and schmit trigger
Comparator gives bad result
E.g. in IR motor speed encoder Unstable region when V1 and
Vref are closed
V1=IR receiver input V+
V0
V1
comparator
Vref
0V
Better output
VUsing Schmit trigger
IR receiver
Signal with noise Schmit trigger
V+
0V=
op-amps (v.5f)
V-
67
Diagram for hysteresis (non-inverting schmit
trigger), see P.420, S. Franco, Design with operational
amplifiers and analog integrated circuits, McGraw Hill.
Voltage
V0
V1
VTH
VTL
Output
Voltage
Switch over
voltage
t
10V
VTH -VTL=
(Vohigh –Volow)(R1/R2)=2V
-10V
VTL
VTH
=-1V
=1V
op-amps (v.5f)
Vref =0
Input voltage
68
Example 4: Schmit trigger using dual-power supply noninverting op amp : A small amount of hysteresis is used to
stabilize the output when V1 is near to Vref.(set R1/R2=0.1)
Vhigh=10V
When Vo =Low(-10Volts), We want to find V
, so
TH(low)
that when V1> VTH(low) Vo will switch from low(10Volts) to high (10Volts).
At opamp V+ input, when V1 is close to VTH(low),
apply current rule :
Vo
Vo
(V1-0)/R1+(V0low-0)/R2 =0; (Note:V1 VTH(low)) 0V=
(VTH(low)-0)/R1+(V0low-0)/R2 =0
Vlow=-10V
(VTH(low)-0)/R1+(-10-0)/R2 =0
VTH(low)=(R1/R2)(10); (NoteR1/R2=0.1)
The op-amp uses V+,V_
VTH(low)= (0.1)(10)=1Volt
power supplies.Output is
So when V1> VTH(low), V0 will switch from low (clamped to Vlow
10V) to high(+10V)
Similarly, VTH(high) =-1Volt , so that when V1< VTH(low) or Vhigh, setVref =0 to make
the math easier
Vo will switch from high(+10volts) to low (-10Volts).
Set R2 >> R1, to make a small hysteresis. Ie. for Schmit
trigger devices R1 0.1*R2, e.g. R1=1K, R2=10K, so the
hysteresis is good enough to reject noise. The diodes are
used to clamp the voltages at +/-10V
69
op-amps (v.5f)
Extra information:
Example 5: Power Transistors
Most op-amps can drive outputs with low currents, we
need transistors to raise the power to drive heavy loads,
e.g. mechanical relays, motors or speakers.
V0=V1-1.2 Volts;
TIP3055 type transistors can drive current up to 15A.
(Note: Transistor TIP3055 is not an op amp, but there are
power op amps , see
http://www.st.com/web/en/catalog/sense_power/FM123/S
C1592)
op-amps (v.5f)
70
Power transistors, from [1]
From: http://www.st.com/stonline/books/pdf/docs/4136.pdf
op-amps (v.5f)
71
From :
http://www.fairchildsemi.com/ds/TI/TIP41C.pdf
op-amps (v.5f)
72
Summary
Studied
Basic digital data acquisition systems
Low-pass, high-pass and band-pass filter design
The configuration of operational amplifier
circuits and their applications
op-amps (v.5f)
73
Appendix
To be discussed in class
op-amps (v.5f)
74
Appendix 1, To prove
1
1
1 ja
1 a2
1/(1+ja)=1/(1+ja)*[(1-ja)/(1-ja)]
= (1-ja)/(12-(ja)2)=(1-ja)/(1+a2), since j2= -1
=1/(1+a2)+(-ja)/(1+a2)=real + imaginary
so
|1/(1+ja)|={real2+ imaginary2}1/2
={[1 /(1+a2)]2+[(-ja)/(1+a2)]2}1/2
={[1+a2]2-(1+a2)a2/[1+a2]2}1/2
={[1+2a2+a4-a2-a4/[1+a2]2}1/2
={[1+a2]/[1+a2]2}1/2
1
1
=1/[1+a2]1/2, proved!
1 ja
1 a2
op-amps (v.5f)
75
ANS: Solution for Exercise 1.5
Gain =Vout/Vin=9V/(10mV*50 °C )=18, set R2/R1=R4/R3=18
How to solve the offset problem.
Sensor V2
Offset of 100mV at V1, 9*Rb/(Ra+Rb)=100mV (make R4>> Ra) why?
Add a small variable resistor Rc between 9V & Ra for offset trimming.
9V
Ra
Rb
V1
Sensor
V2
R2
9V
_
R1
V0
A
+
R3
0V
-9V
R4
op-amps (v.5f)
76
Appendix 2a
Derive the gain formula for the inverting amplifier
To proof: Gain(G) = -R2/R1
Op-amp calculation rules:
(1) Assume ‘+’ and ‘–’ inputs are at the same voltage potential.
(2) The current going into ‘–’ or ‘+’ input of an Op-amp are
assumed to very small (approaching 0).
Kirchhoff current law: The sum of currents entering a point is 0.
Potential at the ‘-’ input is V-=0 (virtual ground, because ‘+’ is also at
0 and they should be the same using rule (1) above, and the current
going into the ‘-’ input is -I3=0 (rule 2) . So using by Kirchhoff current
law (sum of all currents going to a point is 0), I1+I2+I3=0.
So (V1-0)/R1+ (V0-0)/R2+0=0, hence
(V1-0)/R1=-(V0-0)/R2, therefore the amplification=V0/V1=-R2/R1
Virtual-ground,VV1
I2
R1
Input
R3
R2
Output
_
I1 I3
V0
A
+
op-amps (v.5f)
77
Appendix 2b
Derive the gain formula for the non-inverting amplifier
To proof: Gain(G) = 1+(R2/R1)
Op-amp calculation rules:
(1) Assume ‘+’ and ‘–’ inputs are at the same voltage potential.
(2) The current going into ‘–’ or ‘+’ input of an Op-amp are
assumed to very small (approaching 0).
Kirchhoff current law: The sum of currents entering a point is 0.
The potential at the ‘-’ input is V2, it is the same as V1 (rule1), so
V2=V1. The current I3 is 0 (rule2) . So using by Kirchhoff current law
at V2 (sum of all currents going to a point is 0), I1+I2+I3=0.
So (0-V2)/R1+(V0-V2)/R2=0, or (0-V1)/R1+(V0-V1)/R2=0 hence
(V0-V1)/R2=V1/R1, therefore the amplification=V0/V1=1+(R2/R1)
V1
+
Input
_
Output
A
V0
R2
I3
V2 I2 R1
op-amps (v.5f)
I1
78
Appendix 2b
Sketch the Bode plot (frequency response) of a first-order low pass filter
Power gain in dB (20*log10(|Gv(f)|dB ) VS. frequency (log10 scale) plot,
Assume R2=R1 =1K , C=1uF
Gv ( f )
R2 / R1
f
1
fc
2
1
f
1
159
2
, hence Gv ( f )
1
f
1
159
2
From 0 Hz to a point much lower than 159Hz Gain
(e.g. 130 Hz), a horizontal line (0dB), because G(f) in dB
0
f/159<<1, 20*log(|Gv(f)|)
3dB
=20*log10(1)=20*0=0
At f=fc=corner frequency=1/(2R2C)=159Hz,
f/fc=159/159=1, hence power gain=
20*log(1/sqrt(1+1))=20*log (1/1.414) =-3dB
fc Freq.(f)
(half power)
When f>>fc, so (f/ fc)2 >>1, hence power
20 dB/decade
gain= 20*log(fc/f), on the log scale frequency
79
drop line
plot, it is a line of -20dB per decade gradient.
Meaning that, it decreases 20dB for each 10
op-amps (v.5f)
times of frequency increment.



















































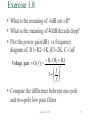






























![Tips on Choosing Components []](http://s1.studyres.com/store/data/007788582_1-9af4a10baac151a9308db46174e6541f-150x150.png)






