Download CHAPTER 11

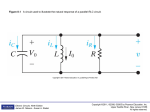
CHAPTER 11
Balanced
Three-Phase Circuits
Electronic Circuits, Tenth Edition
James W. Nilsson | Susan A. Riedel
Copyright ©2015 by Pearson Higher Education.
All rights reserved.
CHAPTER CONTENTS
• 11.1 Balanced Three-Phase Voltages
• 11.2 Three-Phase Voltage Sources
• 11.3 Analysis of the Wye-Wye Circuit
• 11.4 Analysis of the Wye-Delta Circuit
• 11.5 Power Calculations in Balanced Three-Phase
Circuits
• 11.6 Measuring Average Power in Three-Phase
Circuits
Electronic Circuits, Tenth Edition
James W. Nilsson | Susan A. Riedel
Copyright ©2015 by Pearson Higher Education.
All rights reserved.
CHAPTER OBJECTIVES
1. Know how to analyze a balanced, three-phase
wye-wye connected circuit.
2. Know how to analyze a balanced, three-phase wyedelta connected circuit.
3. Be able to calculate power (average, reactive, and
complex) in any three-phase circuit.
Electronic Circuits, Tenth Edition
James W. Nilsson | Susan A. Riedel
Copyright ©2015 by Pearson Higher Education.
All rights reserved.
11.1 Balanced Three-Phase Voltages
• Three sinusoidal voltages
• Identical amplitudes and frequencies
• Out of phase 120° with each other by exactly
• As the a-phase voltage, the b-phase voltage, and the
c-phase voltage.
• abc (or positive) phase sequence
• acb (or negative) phase sequence
Electronic Circuits, Tenth Edition
James W. Nilsson | Susan A. Riedel
Copyright ©2015 by Pearson Higher Education.
All rights reserved.
Figure 11.1
Electronic Circuits, Tenth Edition
James W. Nilsson | Susan A. Riedel
A basic three-phase circuit.
Copyright ©2015 by Pearson Higher Education.
All rights reserved.
abc (or positive) phase sequence
Figure 11.2 Phasor
diagrams of a balanced
set of three-phase
voltages. (a) The abc
(positive) sequence.
Electronic Circuits, Tenth Edition
James W. Nilsson | Susan A. Riedel
Copyright ©2015 by Pearson Higher Education.
All rights reserved.
acb (or negative) phase sequence
Figure 11.2 Phasor
diagrams of a balanced
set of three-phase
voltages. (b) The acb
(negative) sequence.
Electronic Circuits, Tenth Edition
James W. Nilsson | Susan A. Riedel
Copyright ©2015 by Pearson Higher Education.
All rights reserved.
11.2 Three-Phase Voltage Sources
Figure 11.3 A sketch of a threephase voltage source.
Electronic Circuits, Tenth Edition
James W. Nilsson | Susan A. Riedel
Copyright ©2015 by Pearson Higher Education.
All rights reserved.
• There are two ways of interconnecting the separate
phase windings to form a three-phase source: in either
a wye (Y) or a delta (Δ)
• n in Fig. 11.4(a), is called the neutral terminal of the
source.
Figure 11.4 The two basic connections of an ideal
three-phase source. (a) A Y-connected source.
(b) A ∆-connected source.
Electronic Circuits, Tenth Edition
James W. Nilsson | Susan A. Riedel
Copyright ©2015 by Pearson Higher Education.
All rights reserved.
• Three-phase sources and loads can be either Y-
connected or Δ-connected
Electronic Circuits, Tenth Edition
James W. Nilsson | Susan A. Riedel
Copyright ©2015 by Pearson Higher Education.
All rights reserved.
Three-phase source with winding
impedance
Figure 11.5 A model of a three-phase source with winding
impedance: (a) a Y-connected source; and (b) a ∆-connected source.
Electronic Circuits, Tenth Edition
James W. Nilsson | Susan A. Riedel
Copyright ©2015 by Pearson Higher Education.
All rights reserved.
11.3 Analysis of the Wye-Wye Circuit
Figure 11.6
A three-phase Y-Y system.
Electronic Circuits, Tenth Edition
James W. Nilsson | Susan A. Riedel
Copyright ©2015 by Pearson Higher Education.
All rights reserved.
Conditions for a balanced three-phase
circuit
1. The voltage sources form a set of balanced three-
phase voltages. In Fig. 11.6, this means that Va ,n , Vb,n ,
and Vc,n are a set of balanced three-phase voltages.
2. The impedance of each phase of the voltage source
is the same. In Fig. 11.6, this means that Zga = Zgb =
Zgc.
3. The impedance of each line (or phase) conductor is
the same. In Fig. 11.6, this means that Z1a = Z1b = Z1c.
4. The impedance of each phase of the load is the same.
In Fig. 11.6, this means that ZA = ZB = ZC.
Electronic Circuits, Tenth Edition
James W. Nilsson | Susan A. Riedel
Copyright ©2015 by Pearson Higher Education.
All rights reserved.
where
a balanced three phase circuit,
Electronic Circuits, Tenth Edition
James W. Nilsson | Susan A. Riedel
Copyright ©2015 by Pearson Higher Education.
All rights reserved.
• When the system is balanced, the three line currents
are
Electronic Circuits, Tenth Edition
James W. Nilsson | Susan A. Riedel
Copyright ©2015 by Pearson Higher Education.
All rights reserved.
Single-phase equivalent circuit
• The current in the a-phase conductor line is simply
the voltage generated in the a-phase winding of the
generator divided by the total impedance in the aphase of the circuit.
Figure 11.7
A single-phase equivalent circuit.
Electronic Circuits, Tenth Edition
James W. Nilsson | Susan A. Riedel
Copyright ©2015 by Pearson Higher Education.
All rights reserved.
Line-to-line and line-to-neutral voltages
Figure 11.8 Line-to-line and
line-to-neutral voltages.
Electronic Circuits, Tenth Edition
James W. Nilsson | Susan A. Riedel
Copyright ©2015 by Pearson Higher Education.
All rights reserved.
Relationship between line-to-line and
line-to-neutral voltages
1. The magnitude of the line-to-line voltage is 3 times
the magnitude of the line-to-neutral voltage.
2. The line-to-line voltages form a balanced threephase set of voltages.
3. The set of line-to-line voltages leads the set of lineto-neutral voltages by 30°.
Electronic Circuits, Tenth Edition
James W. Nilsson | Susan A. Riedel
Copyright ©2015 by Pearson Higher Education.
All rights reserved.
Phasor diagrams
Figure 11.9 Phasor diagrams showing the relationship
between line-to-line and line-to-neutral voltages in a balanced
system. (a) The abc sequence. (b) The acb sequence.
Electronic Circuits, Tenth Edition
James W. Nilsson | Susan A. Riedel
Copyright ©2015 by Pearson Higher Education.
All rights reserved.
Line voltage v.s. Phase voltage
• Line voltage refers to the voltage across any pair of
lines; phase voltage refers to the voltage across a
single phase.
• Line current refers to the current in a single line;
phase current refers to current in a single phase.
• In a Δ connection, line voltage and phase voltage are
identical.
• In a Y connection, line current and phase current are
identical.
Electronic Circuits, Tenth Edition
James W. Nilsson | Susan A. Riedel
Copyright ©2015 by Pearson Higher Education.
All rights reserved.
Example 11.1
• A balanced three-phase Y-connected generator with
positive sequence has an impedance of 0.2 + j0.5Ω/f
and an internal voltage of 120 V/f The generator
feeds a balanced three-phase Y-connected load
having an impedance of 39 + j28Ω/f. The impedance
of the line connecting the generator to the load is 0.8
+ j1.5Ω/f. The a-phase internal voltage of the
generator is specified as the reference phasor.
a) Construct the a-phase equivalent circuit of the system.
b) Calculate the three line currents IaA, IbB, and IcC.
Electronic Circuits, Tenth Edition
James W. Nilsson | Susan A. Riedel
Copyright ©2015 by Pearson Higher Education.
All rights reserved.
Example 11.1
c) Calculate the three phase voltages at the load, VAN,
VBN, and VCN.
d) Calculate the line voltages VAB, VBC, and VCA at the
terminals of the load.
e) Calculate the phase voltages at the terminals of the
generator, Ian, Ibn, and Icn.
f) Calculate the line voltages Iab, Ibc, and Ica and at the
terminals of the generator.
g) Repeat (a)–(f) for a negative phase sequence.
Electronic Circuits, Tenth Edition
James W. Nilsson | Susan A. Riedel
Copyright ©2015 by Pearson Higher Education.
All rights reserved.
Example 11.1
Figure 11.10 The single-phase
equivalent circuit for Example 11.1.
Electronic Circuits, Tenth Edition
James W. Nilsson | Susan A. Riedel
Copyright ©2015 by Pearson Higher Education.
All rights reserved.
Example 11.1
Electronic Circuits, Tenth Edition
James W. Nilsson | Susan A. Riedel
Copyright ©2015 by Pearson Higher Education.
All rights reserved.
Example 11.1
Electronic Circuits, Tenth Edition
James W. Nilsson | Susan A. Riedel
Copyright ©2015 by Pearson Higher Education.
All rights reserved.
Example 11.1
Electronic Circuits, Tenth Edition
James W. Nilsson | Susan A. Riedel
Copyright ©2015 by Pearson Higher Education.
All rights reserved.
Example 11.1
Electronic Circuits, Tenth Edition
James W. Nilsson | Susan A. Riedel
Copyright ©2015 by Pearson Higher Education.
All rights reserved.
Example 11.1
Electronic Circuits, Tenth Edition
James W. Nilsson | Susan A. Riedel
Copyright ©2015 by Pearson Higher Education.
All rights reserved.
11.4 Analysis of the Wye-Delta Circuit
• When the load is balanced, the impedance of each leg
of the wye is one third the impedance of each leg of
the delta.
• Relationship between three-phase delta-connected
and wye-connected impedance
Electronic Circuits, Tenth Edition
James W. Nilsson | Susan A. Riedel
Copyright ©2015 by Pearson Higher Education.
All rights reserved.
• After the D load has been replaced by its Y equivalent,
the a-phase can be modeled by the single phase
equivalent circuit shown in Fig. 11.11.
Figure 11.11
A single-phase equivalent circuit.
Electronic Circuits, Tenth Edition
James W. Nilsson | Susan A. Riedel
Copyright ©2015 by Pearson Higher Education.
All rights reserved.
• When a load (or source) is connected in a delta, the
current in each leg of the delta is the phase current,
and the voltage across each leg is the phase voltage.
Figure 11.12 A circuit used
to establish the relationship
between line currents and
phase currents in a balanced ∆
load.
Electronic Circuits, Tenth Edition
James W. Nilsson | Susan A. Riedel
Copyright ©2015 by Pearson Higher Education.
All rights reserved.
• To demonstrate the relationship between the phase
currents and line currents, we assume a positive phase
sequence and let If represent the magnitude of the
phase current
Electronic Circuits, Tenth Edition
James W. Nilsson | Susan A. Riedel
Copyright ©2015 by Pearson Higher Education.
All rights reserved.
Electronic Circuits, Tenth Edition
James W. Nilsson | Susan A. Riedel
Copyright ©2015 by Pearson Higher Education.
All rights reserved.
Figure 11.13 Phasor diagrams showing the relationship
between line currents and phase currents in a ∆-connected load.
(a) The positive sequence. (b) The negative sequence.
Electronic Circuits, Tenth Edition
James W. Nilsson | Susan A. Riedel
Copyright ©2015 by Pearson Higher Education.
All rights reserved.
Example 11.2
• The Y-connected source in Example 11.1 feeds a -
connected load through a distribution line having an
impedance of 0.3 + j0.9Ω/f. The load impedance is
118.5 + j85.5Ω/f .Use the a-phase internal voltage of
the generator as the reference.
a) Construct a single-phase equivalent circuit of the
three-phase system.
b) Calculate the line currents IaA, IbB, and IcC.
c) Calculate the phase voltages at the load terminals.
d) Calculate the phase currents of the load.
e) Calculate the line voltages at the source terminals.
Electronic Circuits, Tenth Edition
James W. Nilsson | Susan A. Riedel
Copyright ©2015 by Pearson Higher Education.
All rights reserved.
Example 11.2
Figure 11.14 The
single-phase equivalent
circuit for Example 11.2.
Electronic Circuits, Tenth Edition
James W. Nilsson | Susan A. Riedel
Copyright ©2015 by Pearson Higher Education.
All rights reserved.
Example 11.2
Electronic Circuits, Tenth Edition
James W. Nilsson | Susan A. Riedel
Copyright ©2015 by Pearson Higher Education.
All rights reserved.
Example 11.2
Electronic Circuits, Tenth Edition
James W. Nilsson | Susan A. Riedel
Copyright ©2015 by Pearson Higher Education.
All rights reserved.
Example 11.2
Electronic Circuits, Tenth Edition
James W. Nilsson | Susan A. Riedel
Copyright ©2015 by Pearson Higher Education.
All rights reserved.
Example 11.2
Electronic Circuits, Tenth Edition
James W. Nilsson | Susan A. Riedel
Copyright ©2015 by Pearson Higher Education.
All rights reserved.
Electronic Circuits, Tenth Edition
James W. Nilsson | Susan A. Riedel
Copyright ©2015 by Pearson Higher Education.
All rights reserved.
11.5 Power Calculations in Balanced
Three-Phase Circuits
• Average Power in a Balanced Wye Load
Figure 11.15 A balanced Y load used to introduce
average power calculations in three-phase circuits.
Electronic Circuits, Tenth Edition
James W. Nilsson | Susan A. Riedel
Copyright ©2015 by Pearson Higher Education.
All rights reserved.
Average Power in a Balanced Wye Load
Electronic Circuits, Tenth Edition
James W. Nilsson | Susan A. Riedel
Copyright ©2015 by Pearson Higher Education.
All rights reserved.
Total real power in a balanced threephase load
Electronic Circuits, Tenth Edition
James W. Nilsson | Susan A. Riedel
Copyright ©2015 by Pearson Higher Education.
All rights reserved.
Complex Power in a Balanced Wye Load
• Total reactive power in a balanced three-phase
load
• Total complex power in a balanced threephase
load
Electronic Circuits, Tenth Edition
James W. Nilsson | Susan A. Riedel
Copyright ©2015 by Pearson Higher Education.
All rights reserved.
Power Calculations in a Balanced Delta
Load
Figure 11.16 A ∆-connected load
used to discuss power calculations.
Electronic Circuits, Tenth Edition
James W. Nilsson | Susan A. Riedel
Copyright ©2015 by Pearson Higher Education.
All rights reserved.
Electronic Circuits, Tenth Edition
James W. Nilsson | Susan A. Riedel
Copyright ©2015 by Pearson Higher Education.
All rights reserved.
The total power delivered to a balanced
Δ-connected load
Electronic Circuits, Tenth Edition
James W. Nilsson | Susan A. Riedel
Copyright ©2015 by Pearson Higher Education.
All rights reserved.
Instantaneous Power in Three-Phase
Circuits
• The total instantaneous power is the sum of the
instantaneous phase powers, which reduces to
1.5VmIm cosθf; that is,
• Note this result is consistent with Eq. 11.35 since
Vm  2Vf and I m  2 If .
Electronic Circuits, Tenth Edition
James W. Nilsson | Susan A. Riedel
Copyright ©2015 by Pearson Higher Education.
All rights reserved.
Example 11.3
a) Calculate the average power per phase delivered to
the Y-connected load of Example 11.1.
b) Calculate the total average power delivered to the
load.
c) Calculate the total average power lost in the line.
d) Calculate the total average power lost in the
generator.
e) Calculate the total number of magnetizing vars
absorbed by the load.
f) Calculate the total complex power delivered by the
source.
Electronic Circuits, Tenth Edition
James W. Nilsson | Susan A. Riedel
Copyright ©2015 by Pearson Higher Education.
All rights reserved.
Example 11.3
Electronic Circuits, Tenth Edition
James W. Nilsson | Susan A. Riedel
Copyright ©2015 by Pearson Higher Education.
All rights reserved.
Example 11.3
Electronic Circuits, Tenth Edition
James W. Nilsson | Susan A. Riedel
Copyright ©2015 by Pearson Higher Education.
All rights reserved.
Example 11.3
Electronic Circuits, Tenth Edition
James W. Nilsson | Susan A. Riedel
Copyright ©2015 by Pearson Higher Education.
All rights reserved.
Example 11.4
a) Calculate the total complex power delivered to the Dconnected load of Example 11.2.
b) What percentage of the average power at the sending
end of the line is delivered to the load?
Electronic Circuits, Tenth Edition
James W. Nilsson | Susan A. Riedel
Copyright ©2015 by Pearson Higher Education.
All rights reserved.
Example 11.4
Electronic Circuits, Tenth Edition
James W. Nilsson | Susan A. Riedel
Copyright ©2015 by Pearson Higher Education.
All rights reserved.
Example 11.5
• A balanced three-phase load requires 480 kW at a
lagging power factor of 0.8. The load is fed from a
line having an impedance of 0.005 + j0.025Ω/f. The
line voltage at the terminals of the load is 600V.
a) Construct a single-phase equivalent circuit of the
system.
b) Calculate the magnitude of the line current.
c) Calculate the magnitude of the line voltage at the
sending end of the line.
d) Calculate the power factor at the sending end of the
line.
Electronic Circuits, Tenth Edition
James W. Nilsson | Susan A. Riedel
Copyright ©2015 by Pearson Higher Education.
All rights reserved.
Example 11.5
Figure 11.17 The single-phase
equivalent circuit for Example 11.5.
Electronic Circuits, Tenth Edition
James W. Nilsson | Susan A. Riedel
Copyright ©2015 by Pearson Higher Education.
All rights reserved.
Example 11.5
Electronic Circuits, Tenth Edition
James W. Nilsson | Susan A. Riedel
Copyright ©2015 by Pearson Higher Education.
All rights reserved.
Example 11.5
Electronic Circuits, Tenth Edition
James W. Nilsson | Susan A. Riedel
Copyright ©2015 by Pearson Higher Education.
All rights reserved.
Example 11.5
Electronic Circuits, Tenth Edition
James W. Nilsson | Susan A. Riedel
Copyright ©2015 by Pearson Higher Education.
All rights reserved.
Example 11.5
Electronic Circuits, Tenth Edition
James W. Nilsson | Susan A. Riedel
Copyright ©2015 by Pearson Higher Education.
All rights reserved.
Electronic Circuits, Tenth Edition
James W. Nilsson | Susan A. Riedel
Copyright ©2015 by Pearson Higher Education.
All rights reserved.
11.6 Measuring Average Power in
Three-Phase Circuits
• Electrodynamometer wattmeter:
current coil, potential coil.
• The wattmeter deflects upscale
when
(1) the polarity-marked terminal
of the current coil is toward the
source, and
(2) the polarity-marked terminal
of the potential coil is
connected to the same line in
which the current coil has been
inserted.
Electronic Circuits, Tenth Edition
James W. Nilsson | Susan A. Riedel
Figure 11.18 The key
features of the
electrodynamometer
wattmeter.
Copyright ©2015 by Pearson Higher Education.
All rights reserved.
The Two-Wattmeter Method
• To measure the total power at the terminals of the box,
we need to know n – 1currents and voltages.
Figure 11.19 A general circuit whose
power is supplied by n conductors.
Electronic Circuits, Tenth Edition
James W. Nilsson | Susan A. Riedel
Copyright ©2015 by Pearson Higher Education.
All rights reserved.
Figure 11.20 A circuit used to
analyze the two-wattmeter
method of measuring average
power delivered to a balanced
load.
Electronic Circuits, Tenth Edition
James W. Nilsson | Susan A. Riedel
Copyright ©2015 by Pearson Higher Education.
All rights reserved.
• For a positive phase sequence,
• To find the total power, we add W1 and W2 thus
Electronic Circuits, Tenth Edition
James W. Nilsson | Susan A. Riedel
Copyright ©2015 by Pearson Higher Education.
All rights reserved.
Readings of the two wattmeters
• A closer look at Eqs. 11.58 and 11.59 reveals the
following about the readings of the two wattmeters:
1. If the power factor is greater than 0.5, both
wattmeters read positive.
2. If the power factor equals 0.5, one wattmeter reads
zero.
3. If the power factor is less than 0.5, one wattmeter
reads negative.
4. Reversing the phase sequence will interchange the
readings on the two wattmeters.
Electronic Circuits, Tenth Edition
James W. Nilsson | Susan A. Riedel
Copyright ©2015 by Pearson Higher Education.
All rights reserved.
Example 11.6
• Calculate the reading of each wattmeter in the circuit
in Fig. 11.20 if the phase voltage at the load is 120 V
and (a) Zf  8  j 6 ; (b) Zf  8  j 6 ; (c) Zf  5  j5 3 ;
and (d) Zf  1075 . (e) Verify for (a)–(d) that the
sum of the wattmeter readings equals the total power
delivered to the load
Electronic Circuits, Tenth Edition
James W. Nilsson | Susan A. Riedel
Copyright ©2015 by Pearson Higher Education.
All rights reserved.
Example 11.6
Electronic Circuits, Tenth Edition
James W. Nilsson | Susan A. Riedel
Copyright ©2015 by Pearson Higher Education.
All rights reserved.
Example 11.6
Electronic Circuits, Tenth Edition
James W. Nilsson | Susan A. Riedel
Copyright ©2015 by Pearson Higher Education.
All rights reserved.
Example 11.6
Electronic Circuits, Tenth Edition
James W. Nilsson | Susan A. Riedel
Copyright ©2015 by Pearson Higher Education.
All rights reserved.
Example 11.6
Electronic Circuits, Tenth Edition
James W. Nilsson | Susan A. Riedel
Copyright ©2015 by Pearson Higher Education.
All rights reserved.
Summary
• When analyzing balanced three-phase circuits, the
first step is to transform any connections into Y
connections, so that the overall circuit is of the Y-Y
configuration.
• A single-phase equivalent circuit is used to calculate
the line current and the phase voltage in one phase of
the Y-Y structure. The a-phase is normally chosen for
this purpose.
Electronic Circuits, Tenth Edition
James W. Nilsson | Susan A. Riedel
Copyright ©2015 by Pearson Higher Education.
All rights reserved.
Summary
• Once we know the line current and phase voltage in
the a-phase equivalent circuit, we can take analytical
shortcuts to find any current or voltage in a balanced
threephase circuit, based on the following facts:
 The b- and c-phase currents and voltages are identical to
the a-phase current and voltage except for a 120° shift in
phase. In a positive-sequence circuit, the b-phase quantity
lags the a-phase quantity by 120°, and the c-phase quantity
leads the a-phase quantity by 120°. For a negative sequence
circuit, phases b and c are interchanged with respect to
phase a.
Electronic Circuits, Tenth Edition
James W. Nilsson | Susan A. Riedel
Copyright ©2015 by Pearson Higher Education.
All rights reserved.
Summary
 The set of line voltages is out of phase with the set of phase
voltages by ±30°. The plus or minus sign corresponds to
positive and negative sequence, respectively.
 In a Y-Y circuit the magnitude of a line voltage is 3 times
the magnitude of a phase voltage.
 The set of line currents is out of phase with the set of phase
currents in D-connected sources and loads by 30. The
minus or plus sign corresponds to positive and negative
sequence, respectively.
 The magnitude of a line current is 3 times the magnitude
of a phase current in a D-connected source or load.
Electronic Circuits, Tenth Edition
James W. Nilsson | Susan A. Riedel
Copyright ©2015 by Pearson Higher Education.
All rights reserved.
Summary
• The techniques for calculating per-phase average
power, reactive power, and complex power are
identical to those introduced in Chapter 10.
• The total real, reactive, and complex power can be
determined either by multiplying the corresponding
per phase quantity by 3 or by using the expressions
based on line current and line voltage, as given by
Eqs. 11.36, 11.38, and 11.41.
Electronic Circuits, Tenth Edition
James W. Nilsson | Susan A. Riedel
Copyright ©2015 by Pearson Higher Education.
All rights reserved.
Summary
• The total instantaneous power in a balanced three-
phase circuit is constant and equals 1.5 times the
average power per phase.
• A wattmeter measures the average power delivered to
a load by using a current coil connected in series with
the load and a potential coil connected in parallel with
the load.
• The total average power in a balanced three-phase
circuit can be measured by summing the readings of
two wattmeters connected in two different phases of
the circuit.
Electronic Circuits, Tenth Edition
James W. Nilsson | Susan A. Riedel
Copyright ©2015 by Pearson Higher Education.
All rights reserved.