* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Teknologi Elektrik - ENCON
Variable-frequency drive wikipedia , lookup
Electric machine wikipedia , lookup
War of the currents wikipedia , lookup
Ground loop (electricity) wikipedia , lookup
Induction motor wikipedia , lookup
Electrification wikipedia , lookup
Electric power system wikipedia , lookup
Spark-gap transmitter wikipedia , lookup
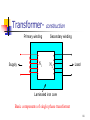
Resistive opto-isolator wikipedia , lookup
Mercury-arc valve wikipedia , lookup
Electrical ballast wikipedia , lookup
Current source wikipedia , lookup
Stepper motor wikipedia , lookup
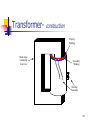
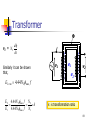
Power electronics wikipedia , lookup
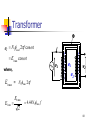
Amtrak's 25 Hz traction power system wikipedia , lookup
Power inverter wikipedia , lookup
Opto-isolator wikipedia , lookup
Ground (electricity) wikipedia , lookup
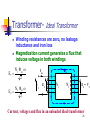
Surge protector wikipedia , lookup
Power engineering wikipedia , lookup
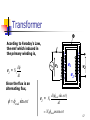
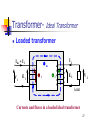
Stray voltage wikipedia , lookup
Buck converter wikipedia , lookup
Distribution management system wikipedia , lookup
Voltage regulator wikipedia , lookup
Electrical substation wikipedia , lookup
Earthing system wikipedia , lookup
Rectiverter wikipedia , lookup
Voltage optimisation wikipedia , lookup
Mains electricity wikipedia , lookup
Resonant inductive coupling wikipedia , lookup
History of electric power transmission wikipedia , lookup
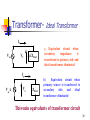
Alternating current wikipedia , lookup
Switched-mode power supply wikipedia , lookup
Chapter 4. Transformer 1 Transformer Introduction Two winding transformers Construction and principles Equivalent circuit Determination of equivalent circuit parameters Voltage regulation Efficiency Auto transformer 3 phase transformer 2 Transformer- Introduction Varieties of transformers 3 Transformer- Introduction 4 Transformer Introduction Transformer is a device that makes use of the magnetically coupled coils to transfer energy It is typically consists of one primary winding coil and one or more secondary windings The primary winding and its circuit is called the Primary Side of the transformer The secondary winding and its circuit is called the Secondary Side of the transformer 5 Transformer Introduction If one of those winding, the primary, is connected to an alternating voltage source, an alternating flux will be produced. The mutual flux will link the other winding, the secondary, and will induced a voltage in it. 6 Transformer- Introduction Transformers are adapted to numerous engineering applications and may be classified in many ways: Power level (from fraction of a volt-ampere (VA) to over a thousand MVA), Application (power supply, impedance matching, circuit isolation), Frequency range (power, audio, radio frequency (RF)) Voltage class (a few volts to about 750 kilovolts) Cooling type (air cooled, oil filled, fan cooled, water cooled, etc.) Purpose (distribution, rectifier, arc furnace, amplifier output, etc.). 7 Transformer Introduction Power transmission 8 Transformer Introduction Power transmission 9 Transformer 4.1 Construction 10 TransformerPrimary winding Supply N1 construction Secondary winding N2 Load Laminated iron core Basic components of single phase transformer 11 Transformer- A) Core type construction B) Shell type Single phase transformer construction 12 Transformer- construction 13 Transformer- construction Primary Winding Multi-layer Laminated Iron Core Secondary Winding H1 H2 X1 X2 Winding Terminals 14 Transformer 4.2 Ideal Transformer 15 Transformer Φ The emf which induced in transformer primary winding is known as self induction emf as the emf is induced due to to flux which produced by the winding itself. i v1 e1 v2 e2 While the emf which induced in transformer secondary winding is known as mutual induction emf as the emf is induced due to to flux which produced by the other winding. 16 Transformer Φ Acording to Faraday’s Law, the emf which induced in the primary winding is, i v1 d e1 = N1 dt e1 v2 e2 Since the flux is an alternating flux, mak sin t e1 = N1 d ( mak sin t ) dt N1mak cos t 17 Transformer Φ e1 N1mak 2f cos t E1max cos t where, E1max = N1max 2f E1rms E1max i v1 e1 v2 e2 4.44 N1max f 2 18 Transformer Φ e2 = N 2 d dt Similarly it can be shown that, E2 rms 4.44 N 2max f E2 4.44 N 2max f N 2 k E1 4.44 N1max f N1 i v1 e1 v2 e2 k is transformation ratio 19 Transformer The voltage ratio of induced voltages on the secondary to primary windings is equal to the turn ratio of the winding turn number of the secondary winding to the winding turn number of the primary winding. Therefore the transformers can be used to step up or step down voltage levels by choosing appropriate number their winding turns. In power system it’s necessary to step up the output voltage of a generator which less than 30kV to up 500kV for long distance transmission. High voltage for long distance power transmission can reduce current flow in the transmission lines, thus line losses and voltage drop can be reduced. 20 Transformer Ideal Transformer Winding resistances are zero, no leakage inductance and iron loss Magnetization current generates a flux that induces voltage in both windings N1 m E1 2 N2 m E2 2 m Im V1 E1 N1 N2 E2 = V2 Current, voltages and flux in an unloaded ideal transformer 21 Transformer Φ Transformer on no load. i v1 e1 v2 e2 22 Transformer Loaded transformer Ideal Transformer Φ2 Φ1 Φ I2 i V1 N1 E2 E1 V2 ZL N2 When a load is connected to the secondary output terminals of a transformer as shown in Figure 4.5, a current I2 flows into the load and into transformer secondary winding N2. The current I2 which flowing in N2 produces flux Φ2 which opposite –by Lenz’s law- to the main magnetic flux Φ in the transformer core. This will weaken or slightly reduce the main flux Φ to Φ’. 23 Transformer Loaded transformer Ideal Transformer Φ2 Φ1 Φ I2 i V1 N1 E2 E1 V2 ZL N2 The reduction of main flux Φ –by Faraday’s law- could also reduce the induced voltage in primary winding E1. Consequently E1 is now smaller than the supply voltage V1, then the primary current would be increased due to that potential differences. Therefore on loaded transformer, the primary current has an additional current of I1’. 24 Transformer Loaded transformer Ideal Transformer Φ2 Φ1 Φ I2 i V1 N1 E2 E1 V2 ZL N2 The extra current I1’ which flowing in the primary winding N1 produces flux Φ1 which naturally react according to Lenz’s law, demagnetize the flux Φ2. Therefore the net magnetic flux in the core is always maintained at original value, it is the main flux Φ (the flux which produced by the magnetizing current). 25 Transformer Loaded transformer Ideal Transformer Φ2 Φ1 Φ I2 i V1 N1 E2 E1 V2 ZL N2 The magneto motive force (mmf) source N2I2 at the secondary winding produces flux Φ2, while the mmf N1I1‘ produces flux Φ1. Since the magnitude of Φ1 equal to magnitude of Φ2 and the reluctance seen by these two mmf sources are equal, thus N 1I 1‘ = N 2I 2 26 Transformer Ideal Transformer Loaded transformer Im + I V1 E1 I2 m 1 1 2 E2 V2 Load Currents and fluxes in a loaded ideal transformer 27 Transformer Ideal Transformer Turn ratio If the primary winding has N1 turns and secondary winding has N2 turns, then: N1 E1 I 2 a N 2 E 2 I1 The input and output complex powers are equal E1 I1* S1 S 2 E2 I*2 28 Transformer Ideal Transformer Functional description of a transformer: When a = 1 Isolation Transformer When | a | < 1 Step-Up Transformer Voltage is increased from Primary side to secondary side When | a | > 1 Step-Down Transformer Voltage is decreased from Primary side to secondary side 29 Transformer Ideal Transformer Transformer Rating Practical transformers are usually rated based on: Voltage Ratio (V1/V2) which gives us the turns-ratio Power Rating, small transformers are given in Watts (real power) and Larger ones (Power Transformers) are given in kVA (apparent power) 30 Transformer Ideal Transformer Example 4.1 Determine the turns-ratio of a 5 kVA 2400V/120V Power Transformer Turns-Ratio = a = V1/V2 = 2400/120 = 20/1 = 20 This means it is a Step-Down transformer 31 Transformer Ideal Transformer Example 4.2 A 480/2400 V (r.m.s) step-up ideal transformer delivers 50 kW to a resistive load. Calculate: (a) the turns ratio, (0.2) (b) the primary current, (104.17A) (c) the secondary current. (20.83A) 32 Transformer Ideal Transformer Nameplate of transformer 33 Transformer Ideal Transformer Equivalent circuit I1 = I2 /T T V1 E1 I2 E2 = V2 V1 = E1 = T E2 Equivalent circuit of an ideal transformer 34 Transformer Ideal Transformer Transferring impedances through a transformer Z1 V1 a V2 V a2 2 I1 I 2 I2 a I1 Vac Z1 a 2 Z load T V1 I2 V2 Zload Equivalent circuit of an ideal transformer 35 Transformer- Ideal Transformer I1 Equivalent circuit when secondary impedance is transferred to primary side and ideal transformer eliminated a) Vac V1 a2Zload I2 Vac/k V2 Zload b) Equivalent circuit when primary source is transferred to secondary side and ideal transformer eliminated Thévenin equivalents of transformer circuit 36 Transformer practical transformer Practical Transformer 37 Transformer 4.3 Equivalent Circuits 38 TransformerR1 equivalent circuit m I1 I2 l2 l1 V1 N1 R2 V2 N2 39 Transformer- equivalent circuit Development of the transformer equivalent circuits The effects of winding resistance and leakage flux are respectively accounted for by resistance R and leakage reactance X (2πfL). X1 R1 V1 X2 I1 R2 I2 V2 N1:N2 40 Transformer practical equivalent circuit In a practical magnetic core having finite permeability, a magnetizing current Im is required to establish a flux in the core. This effect can be represented by a magnetizing inductance Lm. The core loss can be represented by a resistance Rc. 41 TransformerI1 V1 I’1 X1 R1 practical equivalent circuit X2 I0 Ic Rc R2 I2 Im V2 Xm N1:N2 Rc :core loss component, Xm : magnetization component, R1 and X1 are resistance and reactance of the primary winding R2 and X2 are resistance and reactance of the secondary winding 42 Transformer practical equivalent circuit The impedances of secondary side such as R2, X2 and Z2 can be moved to primary side and also the impedances of primary side can be moved to the secondary side, base on the principle of: The power before transferred = The power after transferred. 43 Transformer- practical equivalent circuit The power before transferred = The power after transferred. I22R2 = I1’ 2R2’ Therefore R2’= (I2/ I1’ ) 2 R2 = a2R2 44 Transformer- practical equivalent circuit The turns can be moved to the right or left by referring all quantities to the primary or secondary side. I1 V1 I’1 X1 R1 X’2 R’2 I2 I0 Ic Rc Im Xm V2’ V2 N1:N2 V2' = a V2 , I1' = I2/a X2' = a2 X2 , R2' = a2 R2 a = N1/N2 The equivalent circuit with secondary side moved to the primary. 45 Transformer- Approximate equivalent circuit For convenience, the turns is usually not shown and the equivalent circuit is drawn with all quantities (voltages, currents, and impedances) referred to one side. R1 I1 X1 X’2 I’1 R’2 I0 Ic V1 R c Im Xm V2’ Z2’ N 46 Transformer equivalent circuit Example 4.3 A 100kVA transformer has 400 turns on the primary and 80 turns on the secondary. The primary and secondary resistance are 0.3 ohm and 0.01 ohm respectively and the corresponding leakage reactances are 1.1 ohm and 0.035 ohm respectively. The supply voltage is 2200V. Calculate: (a) the equivalent impedance referred to the primary circuit (2.05 ohm) (b) the equivalent impedance referred to the secondary circuit 47 Transformer 4.4 Determination of Equivalent Circuit Parameter 48 Transformer o/c-s/c tests The equivalent circuit model for the actual transformer can be used to predict the behavior of the transformer. The parameters R1, X1, Rc, Xm, R2, X2 and N1/N2 must be known so that the equivalent circuit model can be used. These parameters can be directly and more easily determined by performing tests: 1. No-load test (or open-circuit test). 2. Short-circuit test. 49 Transformer o/c-s/c tests No load/Open circuit test Provides magnetizing reactance (Xm) and core loss resistance (RC) Obtain components are connected in parallel Short circuit test Provides combined leakage reactance and winding resistance Obtain components are connected in series 50 Transformer open circuit test No load/Open circuit test P oc A X1 R1 X2 R2 W I oc V X Rc m V oc Equivalent circuit for open circuit test, measurement at the primary side. Poc A W V Simplified equivalent circuit Ioc Xm Rc Voc 51 Transformer open circuit test Open circuit test evaluation Poc 0 cos Voc I oc Voc2 Rc Poc 1 Q Voc I oc sin 0 Voc2 Xm Q 52 Transformer short circuit test Short circuit test Secondary (normally the LV winding) is shorted, that means there is no voltage across secondary terminals; but a large current flows in the secondary. Test is done at reduced voltage (about 5% of rated voltage) with full-load current in the secondary. So, the ammeter reads the full-load current; the wattmeter reads the winding losses, and the voltmeter reads the applied primary voltage. 53 Transformer short circuit test Short circuit test P sc A V sc R1 X1 R2 X2 W I sc V Equivalent circuit for short circuit test, measurement at the primary side P A V sc sc R1 X1 a2R2 a2X2 W V I sc Simplified equivalent circuit for short circuit test 54 Transformer short circuit test Short circuit test P A V sc sc Re1 X e1 W I V sc Simplified circuit for calculation of series impedance Re1 R1 a R2 2 X e1 X 1 a X 2 2 Primary and secondary impedances are combined 55 Transformer short circuit test Short circuit test evaluation Psc Re1 2 I sc X e1 2 Z e1 Z e1 Vsc I sc 2 Re1 56 Transformer o/c-s/c tests Equivalent circuit obtained by measurement X e1 Xm R e1 Rc Equivalent circuit for a real transformer resulting from the open and short circuit tests. 57 Transformer o/c-s/c tests Example 4.4 Obtain the equivalent circuit of a 200/400V, 50Hz 1-phase transformer from the following test data:O/C test : 200V, 0.7A, 70W S/C test : 15V, 10A, 85W - on L.V. side - on H.V. side (Rc =571.4 ohm, Xm=330 ohm, Re=0.21ohm, Xe=0.31 ohm) 58 Transformer – voltage regulation Voltage Regulation Most loads connected to the secondary of a transformer are designed to operate at essentially constant voltage. However, as the current is drawn through the transformer, the load terminal voltage changes because of voltage drop in the internal impedance. To reduce the magnitude of the voltage change, the transformer should be designed for a low value of the internal impedance Zeq The voltage regulation is defined as the change in magnitude of the secondary voltage as the load current changes from the no-load to the loaded condition. 59 Transformer – voltage regulation Ze2 I2’ V12’=V20 R1’ Rc’ X1’ Xm’ R2 X2 I2 V2 Z Ze2 = R1’ + R2 + jX1’ + jX2 = Re2 + jXe2 60 Transformer – voltage regulation Ze2 I2’ V12’=V20 Rc’ Applying KVL, Or R1’ X1’ Xm’ R2 X2 I2 V2 Z V20 = I2 (Ze2 ) + V2 = I2 (Re2 + jXe2 ) + V2 V2 = V20 - I2 (Ze2 ) 61 Transformer – voltage regulation I2Xe2 A O θ2 V2 I2Re2 I2 62 Transformer – voltage regulation I2Xe2 V20 I2Xe2 A O θ2 I2Re2 V2 I2Re2 B I2 V20 = I2 (Ze2 ) + V2 = I2 (Re2 + jXe2 ) + V2 63 Transformer – voltage regulation I2Xe2 C V20 θ2 I2Xe2 A O θ2 I2Re2 D N M V2 I2Re2 B L θ2 I2 Voltage drop = AM = OM – OA = AD + DN + NM 64 Transformer – voltage regulation I2Xe2 C V20 θ2 I2Xe2 A O θ2 I2Re2 D M V2 I2Re2 B I2 N L θ2 AD = I2 Re2 cosθ2 DN=BL= I2 Xe2 sinθ2 65 Transformer – voltage regulation I2Xe2 C V20 θ2 I2Xe2 A O θ2 I2Re2 D M V2 I2Re2 B I2 N L θ2 Applying Phytogrus theorem to OCN triangle. (NC)2 = (OC)2 – (ON)2 = (OC + ON)(OC - ON) ≈ 2(OC)(NM) 66 Transformer – voltage regulation I2Xe2 C V20 θ2 I2Xe2 A O θ2 D N M V2 I2Re2 I2Re2 B I2 L θ2 Therefore NM = (NC)2/2(OC) NC = LC – LN = LC – BD = I2 Xe2 cosθ2 - I2 Re2 sinθ2 67 Transformer – voltage regulation I2Xe2 C V20 θ2 I2Xe2 A O θ2 I2Re2 D M V2 I2Re2 B I2 N L θ2 2 I X cos I R sin 2 e 2 2 2 e 2 2 NM = 2V20 AM = AD + DN + NM I 2 X e 2 cos 2 I 2 Re 2 sin 2 2 = I2 Recosθ2 + I2 Xe2 sin θ2 + 2V20 68 Transformer – voltage regulation I2Xe2 C V20 θ2 I2Xe2 A O θ2 I2Re2 D M V2 I2Re2 B thus, votage regulation = (AM)/V20 per unit I2 N L θ2 In actual practice the term NM is negligible since its value is very small compared with V2. Thus the votage regulation formula can be reduced to: 69 Transformer – voltage regulation I2Xe2 C V20 θ2 I2Xe2 A O θ2 N M V2 I2Re2 I2Re2 B L θ2 I2 Voltage regulation = D I 2 Re 2 cos 2 I 2 X e 2 sin 2 V20 70 Transformer voltage regulation The voltage regulation is expressed as follows: Voltage regulation V2 NL V2 L V2 NL V2NL= secondary voltage (no-load condition) V2L = secondary voltage (full-load condition) 71 Transformer voltage regulation For the equivalent circuit referred to the primary: V1 V2' Voltage regulation V1 V1 = no-load voltage V2’ = secondary voltage referred to the primary (full-load condition) 72 Transformer voltage regulation Consider the equivalent circuit referred to the secondary, I2' V2NL R1' X1' X2 Xe2 I2 R2 V2 Z2 Re2 I 2 Re 2 cos 2 I 2 X e 2 sin 2 Voltage regulation V2 NL (-) : power factor leading (+) : power factor lagging 73 Transformer voltage regulation Consider the equivalent circuit referred to the primary, I1 R1 X2' X1 R2' I1' Xe1 V1 V2' Z’2 Re1 Voltage regulation I1 Re1 cos 2 I1 X e1 sin 2 V1 (-) : power factor leading (+) : power factor lagging 74 Transformer voltage regulation Example 4.5 Based on Example 4.3 calculate the voltage regulation and the secondary terminal voltage for full load having a power factor of (i) 0.8 lagging (0.0336pu,14.8V) (ii) 0.8 leading (-0.0154pu,447V) 75 Transformer Efficiency Losses in a transformer Copper losses in primary and secondary windings Core losses due to hysteresis and eddy current. It depends on maximum value of flux density, supply frequency and core dimension. It is assumed to be constant for all loads 76 Transformer Efficiency As always, efficiency is defined as power output to power input ratio output power ( Pout ) input power ( Pin ) Pout Pout losses The losses in the transformer are the core loss (Pc) and copper loss (Pcu). V2 I 2 cos 2 2 V2 I 2 cos 2 Pc I 2 Re 2 77 Transformer Efficiency Efficiency on full load S FL cos FL S FL cos FL Poc Psc where S is the apparent power (in volt amperes) 78 Transformer Efficiency Efficiency for any load equal to n x full load n S FL cos FL 2 n S FL cos FL Poc n Psc where corresponding total loss = Poc n Psc 2 79 Transformer Efficiency Example 4.6 The following results were obtained on a 50 kVA transformer: open circuit test – primary voltage, 3300 V; secondary voltage, 400 V; primary power, 430W.Short circuit test – primary voltage, 124V;primary current, 15.3 A; primary power, 525W; secondary current, full load value. Calculate the efficiency at full load and half load for 0.7 power factor. (97.3%, 96.9%) 80 Transformer Efficiency For constant values of the terminal voltage V2 and load power factor angle θ2 , the maximum efficiency occurs when d 0 dI 2 If this condition is applied, the condition for maximum efficiency is 2 c 2 e2 P I R that is, core loss = copper loss. 81 Transformer- Efficiency 82 Transformer- Auto transformer It is a transformer whose primary and secondary coils are in a single winding Autotransformer 83 Transformer- Auto transformer Same operation as two windings transformer Physical connection from primary to secondary Sliding connection allows for variable voltage Higher kVA delivery than two windings connection 84 Transformer- Auto transformer Advantages: A tap between primary and secondary sides which may be adjustable to provide step-up/down capability Able to transfer larger S apparent power than the two winding transformer Smaller and lighter than an equivalent twowinding transformer Disadvantage: Lacks electrical isolation 85 Transformer- Auto transformer A Step Down Autotransformer: and 86 Transformer- Auto transformer A Step Up Autotransformer: and 87 Transformer- Auto transformer Example 4.7 An autotransformer with a 40% tap is supplied by a 400-V, 60-Hz source and is used for step-down operation. A 5-kVA load operating at unity power factor is connected to the secondary terminals. Find: (a) the secondary voltage, (b) the secondary current, (c) the primary current. 88 Transformer- Auto transformer Solution 89 Transformer -3 phase transformer Three phase transformers The three-phase transformer can be built by: the interconnection of three single-phase transformers using an iron core with three limbs The usual connections for three-phase transformers are: wye / wye seldom used, unbalance and 3th harmonics problem wye / delta frequently used step down.(345 kV/69 kV) delta / delta used medium voltage (15 kV), one of the transformer can be removed (open delta) delta / wye step up transformer in a generation station For most cases the neutral point is grounded 90 Transformer -3 phase transformer Analyses of the grounded wye / delta transformer A VAN Vab a B VB N Vbc b C VC N N Each leg has a primary and a secondary winding. The voltages and currents are in phase in the windings located on the same leg. The primary phase-toline voltage generates the secondary line-toline voltage. These voltages are in phase Vca c 91 Transformer -3 phase transformer Analyses of the grounded wye / delta transformer Ia IA IAN IBN IB Iab ICN Ica I c N Ibc IC Ib 92 Transformer -3 phase transformer Analyses of the grounded wye / delta transformer A VA N VBN VAB C VC N a Vab Vab N B VB C Vbc VCA c Vbc Vca Vbc b 93 Transformer -3 phase transformer Three phase transformer 94 Transformer Three phase transformer 95 Transformer Three phase transformer 96 Transformer Three phase transformer 97 Transformer Three phase transformer 98 Transformer Three phase transformer Transformer Construction Iron Core The iron core is made of thin laminated silicon steel (2-3 % silicon) Pre-cut insulated sheets are cut or pressed in form and placed on the top of each other . The sheets are overlap each others to avoid (reduce) air gaps. The core is pressed together by insulated yokes. 99 Transformer Three phase transformer Transformer Construction Winding The winding is made of copper or aluminum conductor, insulated with paper or synthetic insulating material (kevlar, maylard). The windings are manufactured in several layers, and insulation is placed between windings. The primary and secondary windings are placed on top of each others but insulated by several layers of insulating sheets. The windings are dried in vacuum and impregnated to eliminate moisture. Small transformer winding 100 Transformer Three phase transformer Transformer Construction Iron Cores Three phase transformer iron core The three phase transformer iron core has three legs. A phase winding is placed in each leg. The high voltage and low voltage windings are placed on top of each other and insulated by layers or tubes. Larger transformer use layered construction shown in the previous slides. A B C 101 Transformer Three phase transformer Transformer Construction The dried and treated transformer is placed in a steel tank. The tank is filled, under vacuum, with heated transformer oil. The end of the windings are connected to bushings. The oil is circulated by pumps and forced through the radiators. Three phase oil transformer 102 Transformer Three phase transformer Transformer Construction The transformer is equipped with cooling radiators which are cooled by forced ventilation. Cooling fans are installed under the radiators. Large bushings connect the windings to the electrical system. The oil is circulated by pumps and forced through the radiators. The oil temperature, pressure are monitored to predict transformer performance. Three phase oil transformer 103 Transformer Three phase transformer Dry type transformer Transformer Construction Dry type transformers are used at medium and low voltage. The winding is vacuumed and dried before the molding. The winding is insulated by epoxy resin The slide shows a three phase, dry type transformer. 104