* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Lecture 1 - Digilent Inc.
Radio transmitter design wikipedia , lookup
Integrating ADC wikipedia , lookup
Operational amplifier wikipedia , lookup
Valve RF amplifier wikipedia , lookup
Schmitt trigger wikipedia , lookup
Oscilloscope history wikipedia , lookup
Resistive opto-isolator wikipedia , lookup
Power MOSFET wikipedia , lookup
Power electronics wikipedia , lookup
Surge protector wikipedia , lookup
Surface-mount technology wikipedia , lookup
Opto-isolator wikipedia , lookup
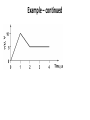
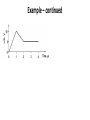
Lecture 15 •Review: •Energy storage and dynamic systems •Basic time-varying signals •Capacitors •Related educational materials: –Chapter 6.3 Dynamic Systems • We now consider circuits containing energy storage elements • The circuits are dynamic systems • They are governed by differential equations • We need to be concerned with the input and output of the system as functions of time • The system output depends upon the state of the system at previous times Basic Time-Varying Signals • Step functions 0 , t 0 u0 ( t ) 1, t 0 • Exponential functions f ( t ) Ae t , t 0 f(t) A 0.368A 0 t Example: Sliding mass with friction • Do forced, natural response; input and output response plots • Time constant and effect of mass on time constant • Notes: – Mention transient, steady-state – Natural vs. forced response – Homogeneous vs. particular solution Energy storage elements – capacitors • Capacitors store energy as an electric field • In general, constructed of two conductive elements separated by a non-conductive material Capacitors • Circuit symbol: • Voltage-charge relation: q( t ) Cv( t ) • Recall: i( t ) dq( t ) dt • So: • C is the capacitance • Units are Farads (F) i( t ) d Cv( t ) C dv( t ) dt dt Capacitor voltage-current relations • Differential form: • Integral form: • Annotate previous slide to show initial voltage, define times on integral, sketchy derivation of integration of differential form to get integral form. Important notes about capacitors 1. If voltage is constant, no current flows through the capacitor • If nothing in the circuit is changing with time, capacitors act as open circuits 2. Sudden changes in voltage require infinite current • The voltage across a capacitor must be a continuous function of time Capacitor Power and Energy • Power: • Energy: t 1 2 Cv ( t ) 2 Example v(t), V • The voltage applied to the capacitor by the source is as shown. Plot the power absorbed by the capacitor and the energy stored in the capacitor as functions of time. 10 5 0 0 1 2 3 4 Time, ms Example – continued Example – continued Series combinations of capacitors + v1(t) - + v2(t) + vN(t) - Series combinations of capacitors • A series combination of capacitors can be represented as a single equivalent capacitance Þ Parallel combinations of capacitors i1(t) i2(t) iN(t) Parallel combinations of capacitors • A parallel combination of capacitors can be represented as a single equivalent capacitance Þ Example • Determine the equivalent capacitance, Ceq