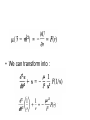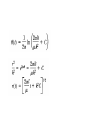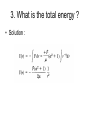Download Central Force

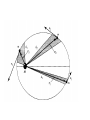
Central Force
Umiatin,M.Si
• The aim : to evaluate characteristic
of motion under central force field
A. Introduction
• Central Force always directed along the
line connecting the center of the two
bodies
• Occurs in : motion of celestial bodies and
nuclear interaction
Central Force Motion as One Body Problem
• Suppose isolated system consist two
bodies and separated a distance r = |r|
with interaction between them described
by a central force F(r), we need six
quantities used to describe motion of
those particle :
Method 1 :
• To describe those, we need six quantities (
three component of r1 and three
component of r2). The equation of motion
of those particle are :
• If F(r) > 0: repusive , F(r) <0 : Attractive.
Coupled by :
Method 2
• Describe a system using center mass (R)
and relative position (r).
• R describes the motion of the center of
mass and r describes the relative motion
of one particle with respect to the other
No external forces are acting on the
system, so the motion of the center of
mass is uniform translational motion.
R** = 0.
• Where reduced mass define by :
• Two bodies problem has been simplified
into one body problem.
• Solve the equation of motion :
• The center of mass moves with uniform velocity :
• By choosing the initial condition, vo, to, Ro = 0,
the origin of coordinate coincides with center of
mass R.
• So the position of m1 and m2 which
measured from center of mass :
If m2 >> m1, then reduced mass:
The eq of motion :
Become :
• Hence the problem can be treated as a
one body problem. Thus, whenever we
use mass m instead of µ, we are indicating
that the other mass is very large, whereas
the use of µ indicates that either the two
masses are comparable.
B. General properties of Central Force
1. Central Force is Confined to a Plane
If p is the linear momentum of a particle
of mass µ, the torque τ about an axis
passing through the center of force is :
• If the angular momentum L of mass µ is
constant, its magnitude and direction are fixed in
space. Hence, by definition of the cross product,
if the direction of L is fixed in space, vectors r
and p must lie in a plane perpendicular to L.
That is, the motion of particle of mass µ is
confined to a plane that is perpendicular to L.
• As we the force acting at body is central
force, three dimensional problem can be
reduced into two dimensional. Using polar
coordinate system :
2. Angular Momentum and Energy are Constant
The angular momentum of a particle of mass
µ at a distance r from the force center is :
• Since there are no dissipative systems
and central forces are conservative, the
total energy is constant :
3. Law of Equal Areas
Consider a mass µ at a distance r(θ) at
time t from the force center O :
• Subtituting
C. Equation of Motion
From the previous description :
• If we know V(r), these equations can be
solved for θ(t) and r(t). The set [θ(t), r(t)]
describes the orbit of the particle.
• Solve the equation, we find :
• We will get t(r) then inverse r(t). But we
are interested in the equation of the path
in term r and θ
• We may write :
• And subtitute :
• Then :
Suppose the Force is F(r) = Krn
• K = constant
• If n = 1  the solution is motion of
harmonic oscillator
• If n = -2 , eq : coulomb and gravitation
force
Other method : Use Lagrangian
• Lagrangian of the system :
• We find
• To simplify, use other variable, for example
: u in which = 1/r
• Next find
• Therefore :
• We can transform into :
Example
1. Find the force law for a central force field
that allow a particle to move in logarithmic
spiral orbit given by (k and α are constant)
:
• Solution :
First determine :
• Now determine :
2. Find r(t) and θ(t) !
Solution :
3. What is the total energy ?
• Solution :
• We know that
D. Planetary Motion
The equation for the path of a particle
moving under the influence of a central
force whose magnitude is inversely
proportional to the distance between the
particle can be obtain from :
• If we define the origin of θ so that the
minimum value of r occurs at θ = 0, so