Download phy201_5 - Personal.psu.edu

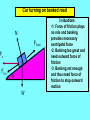
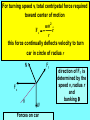
Physics 211
5: Some Application of Newtons
Laws
•Newtons Second law and uniform circular motion
•Newtons Second law and non uniform circular motion
•Motion in accelerated Frames of Reference
•Motion in the presence of resistive forces.
In uniform circular motion the
acceleration of the object is
v2 ˆ
ac = r
r
rˆ is the unit vector pointing from the
center of motion to the object
What causes this acceleration?
It must be a force
2
v
m
Fc = rˆ
r
where m is the mass of the object.
This force is called the CENTRIPETAL
force
Where do centripetal forces come from?
gravity
tension
friction
v
W
W = mac = mg (r)

v2
mg ( ) = m
r

v=
rg(r) in order that gravitational force
sustains uniform circular motion
Vertical Rotation at
constant speed
T
v
W
Wt
= mat = 0
T + Wc = mac
v2
=m
r
Horizontal Rotation
v
T
T = mac
2
v
=m
r
v=
rT
m
If speed increases and length of string is
fixed then the tension increases
Car turning on flat road
v
Ff
v2
F f = mac = m
r
rF f
v=
m
If the speed increases and the force of friction
does not the radius of turning increases (skidding
outward)
Car turning on banked road
N
Ff,out
Fc
Ff,in

W
3 situations
•1: Force of friction plays
no role and banking
provides necessary
centripetal force
•2: Banking too great and
need outward force of
friction
•3: Banking not enough
and thus need force of
friction to stop outward
motion
For turning speed v, total centripetal force required
toward center of motion
mv2
Fc = rˆ
r
this force continually deflects velocity to turn
car in circle of radius r
N
Ff
Fc

W
Forces on car
direction of Ff is
determined by the
speed v, radius r
and
banking 
Fc = N + Ff + W
resolving vertically
0 = N cos  +Ff sin  - mg
= N cos  + mNsin - mg
resolving horizontally
m v2
= N sin  - Ff cos 
r
= Nsin - m N cos 
case 1: Ff = 0
 N cos 
mv
= mg
2
r
= N sin 

 v2
g
tan


=

 r

  = tan
-1
2
v


gr 
case 2 and 3: fixed r,v and  and we want to find
minimum friction for no slipping
(out or in )
(i ) Ncos  + m Nsin  - mg = 0
mv 2
(ii) N sin - m N cos =0
r
v2

+ mg
tan  = r
2
v
g
m

r
2
v
(i )
- (ii )  g  
2
v
r
gtan  
r
m = 2
v

tan  + g

r
Motion in the Presence of
resistive Forces.
R = - bv
consider object dropping in air or a liquid
Total vertical force
Newtons 2nd law
= b v - mg
dv
 m
= b v - mg
dt
dv
bv
- g  Differential Equation

=
dt
m
which has the solution
mg
- bt
v(t ) =
1-e m
b
(
)