* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Derivation Applications of Bernoulli Principal
Classical central-force problem wikipedia , lookup
Relativistic quantum mechanics wikipedia , lookup
Lift (force) wikipedia , lookup
Biofluid dynamics wikipedia , lookup
Reynolds number wikipedia , lookup
History of fluid mechanics wikipedia , lookup
Blade element momentum theory wikipedia , lookup
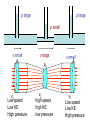
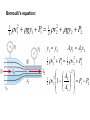
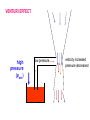
Lesson Opener: How does a plane fly? How does a perfume spray work? Why does a cricket ball curve? Derivation and Applications of the Bernoulli Principal NIS Taldykorgan Grade 11 Physics Lesson Objective: Daniel Bernoulli (1700 – 1782) 1.To apply Bernoulli’s equation to solve problems 2.To describe Bernoulli’s principle and to derive his formula in terms of conservation of energy 3.To present applications of the Bernoulli principle Bernoulli’s Principle As the speed of a fluid goes up, its pressure goes down! The pressure in a fast moving stream of fluid is less than the pressure in a slower stream Fast stream = low air pressure Slow stream = High air pressure p large p large p small v small A1 v large v1 Low speed Low KE High pressure v2 high speed high KE low pressure A2 v small A1 v1 Low speed Low KE High pressure Equation of Continuity Bernoulli’s Equation in terms of Fluid Energy “for any point along a flow tube or streamline” P + ½ v2 + g h = constant Each term has the dimensions of energy / volume or energy density. ½ v 2 KE of bulk motion of fluid gh GPE for location of fluid P pressure energy density arising from internal forces within moving fluid (similar to energy stored in a spring) Transformation of SI Units to Joule/meter3= energy/volume: P [Pa] = [N m-2] = [N m m-3] = [J m-3] ½ v2 [kg m-3 m2 s-2] = [kg m-1 s-2] = [N m m-3] = [J m-3] gh [kg m-3 m s-2 m] = [kg m s-2 m m-3] = [N m m-3] = [J m-3] Deriving Bernoulli’s starting with the law of continuity For an " incompress ible" fluid : (constant) Consider a given mass of fluid M V1 V2 M A1x1 A2 x2 M A1v1t A2 v2 t A1v1 A2 v2 Bernoulli’s Equation For steady flow, the velocity, pressure, and elevation of an incompressible and nonviscous fluid are related by an equation discovered by Daniel Bernoulli (1700–1782). Deriving Bernoulli’s equation as Conservation of Energy Energy - work relationsh ip on " piece" of fluid M K i U i Wi f K f U f K1 U1 W12 K 2 U 2 1 2 Mv12 Mgy1 P2 P1 V 1 2 Mv Mgy 2 2 2 M V 1 2 v12 gy1 P2 P1 12 v22 gy2 1 2 v12 gy1 P1 12 v22 gy2 P2 Bernoulli’s equation: 1 2 v gy1 P1 v gy2 P2 2 1 2 2 1 2 y1 y2 1 2 A1v1 A2v2 v P1 v P2 2 1 1 2 2 2 A 2 2 2 1 P P v 1 2 1 2 2 A1 BERNOULLI’S EQUATION V12 V22 p1 p2 2 2 2 V Constant p 2 • In a moving fluid p+½V2 = constant everywhere • An increase in velocity of the fluid results in a decrease in pressure • Bernoulli’s equation is an extension of F=ma for fluid flows and aerodynamics HOW DOES A WING GENERATE LIFT? • An imbalance of pressure over the top and bottom surfaces of the wing. – If the pressure above is lower than the pressure on bottom surface, lift is generated Airplane Wing is curved on top HOW DOES A CURVED WING GENERATE LIFT? Flow velocity over the top of wing is faster than over bottom surface – Air over wing is squashed to smaller crosssectional area – Mass continuity AV=constant, velocity must increase force high speed low pressure force What happens when two ships or trucks pass alongside each other? VENTURI EFFECT high pressure (patm) low pressure velocity increased pressure decreased artery Flow speeds up at constriction Pressure is lower Internal force acting on artery wall is reduced External forces causes artery to collapse Arteriosclerosis and vascular flutter References and links: • Bernoulli Activity: • http://mitchellscience.com/bernoulli_principle_discussion _nomath • Steve Spangler and Hydrogen Hexafluoride: • http://www.youtube.com/watch?v=GRLOgmmz_EU • Phet Colorado Fluid Pressure and Flow simulation: • http://phet.colorado.edu/en/simulation/fluid-pressureand-flow • Types of Fluids: http://mechteacher.com/fluid/#ixzz2fcgGwLbq • Flowing Fluids,Laminar Flow and stream lines: • http://www.youtube.com/watch?v=_aWdeXby7CA