Download Derivation Applications of Bernoulli Principal

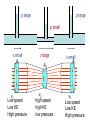
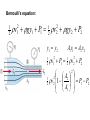
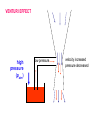
Lesson Opener:
How does a plane fly?
How does a perfume spray work?
Why does a cricket ball curve?
Derivation and
Applications of the
Bernoulli Principal
NIS Taldykorgan
Grade 11 Physics
Lesson Objective:
Daniel Bernoulli (1700 – 1782)
1.To apply Bernoulli’s
equation to solve problems
2.To describe Bernoulli’s principle and to derive his
formula in terms of conservation of energy
3.To present applications of the Bernoulli principle
Bernoulli’s Principle
As the speed of a fluid goes up, its
pressure goes down!
The pressure in a fast moving
stream of fluid is less than the
pressure in a slower stream
Fast stream = low air pressure
Slow stream = High air pressure
p large
p large
p small
v small
A1
v large
v1
Low speed
Low KE
High pressure
v2
high speed
high KE
low pressure
A2
v small
A1
v1
Low speed
Low KE
High pressure
Equation of Continuity
Bernoulli’s Equation in terms of Fluid Energy
“for any point along a flow tube or streamline”
P + ½  v2 +  g h = constant
Each term has the dimensions of energy / volume or energy density.
½  v 2 KE of bulk motion of fluid
gh
GPE for location of fluid
P
pressure energy density arising from internal forces within
moving fluid (similar to energy stored in a spring)
Transformation of SI Units to Joule/meter3= energy/volume:
P
[Pa] = [N m-2] = [N m m-3] = [J m-3]
½  v2
[kg m-3 m2 s-2] = [kg m-1 s-2] = [N m m-3] = [J m-3]
gh
[kg m-3 m s-2 m] = [kg m s-2 m m-3] = [N m m-3] = [J m-3]
Deriving Bernoulli’s starting with
the law of continuity
For an " incompress ible" fluid :
  (constant)
Consider a given mass of fluid
M  V1  V2
M  A1x1  A2 x2
M  A1v1t  A2 v2 t
 A1v1  A2 v2
Bernoulli’s Equation
For steady flow, the velocity, pressure, and
elevation of an incompressible and nonviscous
fluid are related by an equation discovered by
Daniel Bernoulli (1700–1782).
Deriving Bernoulli’s equation as Conservation of Energy
Energy - work relationsh ip on
" piece" of fluid M
K i  U i  Wi  f  K f  U f
K1  U1  W12  K 2  U 2
1
2
Mv12  Mgy1  P2  P1 V 
1
2
Mv  Mgy 2
2
2
M  V
1
2
v12  gy1  P2  P1   12 v22  gy2
1
2
v12  gy1  P1  12 v22  gy2  P2
Bernoulli’s equation:
1
2
v  gy1  P1  v  gy2  P2
2
1
2
2
1
2
y1  y2
1
2
A1v1  A2v2
v  P1  v  P2
2
1
1
2
2
2
  A 2 
2
2
1
 P P



v
1

2
1
2
2


  A1  


BERNOULLI’S EQUATION
V12
V22
 p1  
p2  
2
2
2
V
Constant
p
2
• In a moving fluid p+½V2 = constant everywhere
• An increase in velocity of the fluid results in a decrease in
pressure
• Bernoulli’s equation is an extension of F=ma for fluid
flows and aerodynamics
HOW DOES A WING GENERATE LIFT?
• An imbalance of pressure over the top and
bottom surfaces of the wing.
– If the pressure above is lower than the pressure on
bottom surface, lift is generated
Airplane Wing is curved on top
HOW DOES A CURVED WING GENERATE LIFT?
Flow velocity over the top of wing is faster than
over bottom surface
– Air over wing is squashed to smaller crosssectional area
– Mass continuity AV=constant, velocity must
increase
force
high speed
low pressure
force
What happens when two ships or trucks pass alongside each other?
VENTURI EFFECT
high
pressure
(patm)
low pressure
velocity increased
pressure decreased
artery
Flow speeds up at
constriction
Pressure is lower
Internal force acting on
artery wall is reduced
External forces causes
artery to collapse
Arteriosclerosis and vascular flutter
References and links:
• Bernoulli Activity:
• http://mitchellscience.com/bernoulli_principle_discussion
_nomath
• Steve Spangler and Hydrogen Hexafluoride:
• http://www.youtube.com/watch?v=GRLOgmmz_EU
• Phet Colorado Fluid Pressure and Flow simulation:
• http://phet.colorado.edu/en/simulation/fluid-pressureand-flow
• Types of Fluids:
http://mechteacher.com/fluid/#ixzz2fcgGwLbq
• Flowing Fluids,Laminar Flow and stream lines:
• http://www.youtube.com/watch?v=_aWdeXby7CA