Download Energy3

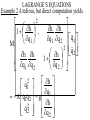
STATIC EQUILIBRIUM
[4] Calkin, M. G. “Lagrangian and Hamiltonian
Mechanics”, World Scientific, Singapore, 1996,
ISBN 981-02-2672-1
Consider an object having mass M held in the air at
height y > 0 above the ground and released. Energy
conservation implies that its height y(t) as a function
of time t > 0 since release must satisfy the equation
d
dt

1
2

My  Mgy  My (y  g)  0
2
Since this equation holds if and only if either
y  0 or My  Mg  Force,
energy conservation doesn’t imply Newtons 2nd law
STATIC EQUILIBRIUM
  0  My  gM ,
We observe that y
and, for an unconstrained object having mass M,
position r (a vector), and a position dependent
potential energy U(r), we observe that energy
conservation implies that
r  0 

U
Mr  
 Force
r
An object is said to be in static equilibrium if its
position r is constant. Therefore, if a system is not
in static equilibrium then energy conservation
implies Newton’s 2nd law.
ENERGY NOT ENOUGH
We made the painful observation, that conservation
of energy by itself does not suffice to explain the
real world in which things happen: rain falls from
the sky and objects move when they are pushed
Definition A virtual displacement r of an object
is any change of its position that can be imagined
without violating any specific constraint. The virtual
work W  F  r is the scalar product of the
force F and the virtual displacement
Examples Virtual displacements for a falling object are
arbitrary vectors, but those for an object that is
constrained to lie on a table must be horizontal
STATIC PRINCIPLE OF VIRTUAL WORK
Fundamental Principle: An object is in static
equilibrium only if the virtual work associated with
every virtual displacement is zero
Example 1 Consider an unconstrained object that is
subjected to a force F. Then, if the object is in static
equilibrium, we obtain from the principle above that
F  r  0
for every virtual displacement r. Therefore, since
the object is unconstrained we may choose r  F
to obtain that F  F  0 hence F  0
STATIC PRINCIPLE OF VIRTUAL WORK
Example 2 Consider an object that is constrained to lie
on a table surface that is flat. Assume that the only
force on the object is the gravitational force F. Then if
the object is in static equilibrium
F  r  0
for every virtual displacement r. Since the
object is constrained to lie on the table surface, the
virtual displacements consist of all vectors parallel to
the table. Therefore, if the object is in static
equilibrium F must be orthogonal to the table
surface. (Recall that two vectors are orthogonal if
and only if their scalar product equals zero)
STATIC PRINCIPLE OF VIRTUAL WORK
Example 3 This example shows that the static
principle of virtual work applies to systems consisting
of one or more objects that may be mutually as well as
individually constrained. Consider two weights
attached by a flexible rope as illustrated below.
gravitational
W
2
W1
force
L1
L2
Let the configuration of the system be represented
by a vector r  ( y1 , y 2 ) whose coordinates are
the heights of each object. If the system is in static
equilibrium what is the ratio of the weights ?
STATIC PRINCIPLE OF VIRTUAL WORK
Example 4 Consider two weights on a pulley as
illustrated in the figure below
gravitational
force
W1
W2
If the system is in static equilibrium what is the
ratio of the weights ?
D’ALEMBERT’S PRINCIPLE
Definition For a moving object
the force of constraint is
F
( con)
 mr  F
( applied)
D’Alemberts Principle: The virtual work done by
force of constraint equals zero, this means that
 r  0
for every virtual displacement r
(con)
F
This is a dynamic principle of virtual work. It can
be extended to describe systems with many objects.
D’ALEMBERT’S PRINCIPLE
Example 1 An object slides on an inclined plane
(x, y -horizontal coordinates) having angle 
r  [x y z], z  x tan , r  [x y x tan ]
F
( con)
 M[x y x tan ]  [0 0  Mg ]
and D’Alembert’s principle implies that
F
( con)
 [x y x tan ]  0, x, y
therefore the equations of motion are
x  g sin  cos , y  0, z  g(sin )
2
GENERALIZED COORDINATES
The configuration of a system with N objects having
masses m1 , , m N whose positions r1 , , rN
are constrained by 3N-f independent functions
Gi (r1,, rN , t )  0,
i  1,  ,3 N  f
can be parameterized by f independent variables
rj  rj (q1 ,, q f , t ),
j  1,  , N
Virtual displacements, expressed in GC, are
m
r  [r1 ,, rn ] 

i 1
r1
rm
[
, ,
] q i
q i
q i
LAGRANGE’S EQUATIONS
D’Alembert’s principle expressed in GC has the form
f  N

rj

( applied) 
(m jrj  Fj
)  q i  0

q i


i 1  j1


Therefore, the chain rule for derivatives implies that
d  T

dt  q i
N
T 
j1
  T  Q , i  1,  , f
 q
i
i

m j r j r j
2
N
, Qi  
rj
j1 q i
(app)
Fj
,i
 1,..., N
LAGRANGE’S EQUATIONS
D’Alembert’s Principle implies, but can NOT be
derived from Newton’s 2nd Law. However, it can be
derived from conservation of energy together with the
static principle of virtual work by defining constraints
as the limit of forces orthogonal to the constraint set.
If each applied force is conservative then there exists a
potential energy function U(r , , r ) such that
1
N

U

U
Fj

, j  1,..., N  Qi 
, i  1,..., f
r j
q i
This is the reason Q i are called generalized forces.
(app)
LAGRANGE’S EQUATIONS
Example 1 Consider a single unconstrained object with
mass M and position r. We can choose q = r to obtain
( app)

T

T
1
 0, Q  F
T  Mr  r,   Mr,
r
r
2
Therefore, Lagrange’s Equations reduce to Newton’s
Second Law
d T  Mr  F(app)
dt r

T
, i  1,..., f are called
This is the reason p i 
q i
generalized momenta.
LAGRANGE’S EQUATIONS
Example 2 Compute the trajectory of an object with
mass M sliding on a surface whose height = h(x,y)
(x and y are horizontal coordinates)
Choose generalized coordinates q1  x, q 2  y
Then the kinetic energy
2



2
2 
M

T
q 1  q 2  q 1 h q 2 h  
q 2  
2
 q1


And the generalized momenta
    h  h  h 
pi  M q i  q1 q 2
,
i  1, 2



q

q
1
2

 q i 

LAGRANGE’S EQUATIONS
Example 2 For i=1,2 the generalized force
T

h
Q i  g
,
q i
2
2
h
h
 h
 h
 M ( q 1
 q 2
)(q 1
 q 2
)
q1
q 2
q1q i
q 2 q i
q i
and Lagrange’s Equations
d p  T  g h
i
q i
dt
qi
are a pair of second order differential equations.
LAGRANGE’S EQUATIONS
Example 2 A tedious, but direct computation yields
  h 


h

h
,
1  
 q

q1 
q1 q 2  1 


M
2 q 
 h h
 2 



h
1 

 q q

 q 2  
 1 2
2
2

h



 q1 
q1 



  A q 1q 2  g 
h 
 2 
 q 2   q 



2

LAGRANGE’S EQUATIONS
Example 2 where A is the 2 x 3 matrix with entries

h

h
A11  4
,
q1q1 q1
2

h

h

h

h
4
2
q1q 2 q1
q1q1 q 2
2
A12
2

h

h

h

h
A13  2

q1q 2 q 2 q 2 q 2 q1
2
2
LAGRANGE’S EQUATIONS
Example 2

h

h

h

h
A 21  2

,
q1q 2 q1 q1q1 q 2
2

h

h

h

h
4
2
,
q1q 2 q 2
q 2 q 2 q1
2
A 22
2

h

h
A 23  4
.
q 2 q 2 q 2
2
2
GEODESICS AND GENERAL RELATIVITY
If we set g = 0 in Example 2 we obtain the equations
for a geodesic trajectory on the surface, that is the
uniform speed trajectory whose distance between any
two points is minimal.
Albert Einstein showed that an object in any inertial
frame, such as in space moving with constant speed
or falling freely under the Earths gravity, follows a
geodesic trajectory. This is how he explained the
equivalence between gravitational and inertial mass
that was measured by experimentalists with such
amazing precision.
HAMILTON’S EQUATIONS AND ENERGY
If, as in Example 2, the kinetic energy is a quadratic
function of the generalized velocities and the forces
are conservative (arising from a potential energy U)
then the total energy is given by the Hamiltonian
H  U  T  i1 pi q i .
i f
The system dynamics satisfies Hamilton’s equation
 H 
q i   0 1  q i 
p    1 0  H  ,

 i 


p
 i
i  1,  , f,
the foundation of advanced and quantum mechanics.