Download The solar dynamo(s) - Center for Magnetic Self Organization

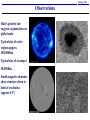
Chicago 2003
The solar dynamo(s)
Fausto Cattaneo
Center for Magnetic Self-Organization in Laboratory
and Astrophysical Plasmas
[email protected]
Chicago 2003
The solar dynamo problem
The solar dynamo is invoked to explain the origin magnetic
activity
Three important features:
• Wide range of spatial scales. From global scale to limit of
resolution
• Wide range of temporal scales. From centuries to
minutes
• Solar activity is extremely well documented
Models are strongly observationally constrained
Chicago 2003
Observations
Hale’s polarity law
suggests organization on
global scale.
Typical size of active
regions approx
200,000Km
Typical size of a sunspot
50,000Km
Small magnetic elements
show structure down to
limit of resolution
(approx 0.3")
Chicago 2003
Observations: large scale
• Active regions migrate from midlatitudes to the equator
• Sunspot polarity opposite in two
hemispheres
• Polarity reversal every 11 years
Chicago 2003
Observations: large scale
PROXY DATA OF SOLAR MAGNETIC ACTIVITY AVAILABLE
10
Be : stored in ice cores after 2 years in atmosphere
14
C : stored in tree rings after ~30 yrs in atmosphere
Beer (2000)
Wagner et al (2001)
Cycle persists through
Maunder Minimum (Beer et al 1998)
Chicago 2003
Observations: small scale
Two distinct scales of convection (maybe more)
• Supergranules:
– not visible in intensity
– 20,000 km typical size
– 20 hrs lifetime
– weak dependence on latitude
• Granules:
– strong contrast
– 1,000km typical size
– 5 mins lifetime
– homogeneous in latitude
Chicago 2003
Observations: small scale
Quiet photospheric flux
• Network fields
– emerge as ephemeral regions (possibly)
– reprocessing time approx 40hrs
– weak dependence on solar cycle
• Intra-network magnetic elements
– possibly unresolved
– typical lifetime few mins
Chicago 2003
General dynamo principle
Any three-dimensional, turbulent (chaotic) flow with high magnetic Reynolds
number is (extremely) likely to be a dynamo.
• Reflectionally symmetric flows:
– Small-scale dynamo action
– Disordered fields; same correlation length/time as turbulence
2
2
B
– Generate | B | but not
• Non-reflectionally symmetric flows:
– Large-scale dynamo; inverse cascade of magnetic helicity
– Organized fields; correlation length/time longer than that of turbulence
– Possibility of
| B |2  B
2
Chicago 2003
Rotational constraints
In astrophysics lack of reflectional symmetry associated with
(kinetic) helicity  Coriolis force  Rotation
Introduce Rossby radius Ro (in analogy with geophysical flows)
• Motions or instabilities on scales  Ro “feel’’ the rotation.
– Coriolis force important  helical motions
– Inverse cascades  large-scale dynamo action
• Motions or instabilities on scales < Ro do not “feel” the rotation.
– Coriolis force negligible  non helical turbulence
– Small-scale dynamo action
Chicago 2003
Modeling: large-scale generation
Dynamical ingredients
• Helical motions: Drive the α-effect. Regenerate poloidal
fields from toroidal
• Differential rotation: (with radius and/or latitude)
Regenerate toroidal fields from poloidal. Probably
confined to the tachocline
• Magnetic buoyancy: Removes strong toroidal field from
region of shear. Responsible for emergence of active
regions
• Turbulence: Provides effective transport
Chicago 2003
Modeling: helical motions
• Laminar vs turbulent α-effect:
– Babcock-Leighton models. α-effect driven by rise and twist of large
scale loops and subsequent decay of active regions. Coriolis-force
acting on rising loops is crucial. Helical turbulence is irrelevant.
Dynamo works because of magnetic buoyancy.
– Turbulent models. α-effect driven by helical turbulence. Dynamo
works in spite of magnetic buoyancy.
• Nonlinear effects:
– Turbulent α-effect strongly nonlinearly
suppressed
– Interface dynamos?
– α-effect is not turbulent (see above)
Cattaneo & Hughes
Chicago 2003
Modeling: differential rotation
• Latitudinal differential rotation:
– Surface differential rotation persists throughout the convection zone
– Radiative interior in solid body rotation
Schou et al.
• Radial shear:
– Concentrated in the tachocline; a thin
layer at the bottom of the convection
zone
– Whys is the tachocline so thin? What
controls the local dynamics?
No self-consistent model for the solar differential rotation
Chicago 2003
Modeling: magnetic buoyancy
What is the role of magnetic buoyancy?
• Babcock-Leighton models:
– Magnetic buoyancy drives the dynamo
– Twisting of rising loops under the action of the Coriolis force generates
poloidal field from toroidal field
– Dynamo is essentially non-linear
• Turbulent models:
– Magnetic buoyancy limits the growth of the
magnetic field
– Dynamo can operate in a kinematic regime
Wissink et al.
Do both dynamos coexist? Recovery from Maunder minima?
Chicago 2003
Modeling: turbulence
How efficiently is turbulent transport?
• Babcock-Leighton models: Turbulent diffusion causes the dispersal of
active regions. Transport of poloidal flux to the poles.
• Interface models: Turbulent diffusion couples the layers of toroidal
and poloidal generation
• All models:
– Turbulent pumping helps to keep
the flux in the shear region
– Turbulence redistributes angular
momentum
– Etc. etc. etc.
Tobias et al.
Chicago 2003
Modeling: challenges
No fully self-consistent model exists.
• Self-consistent model must capture all dynamical
ingredients (MHD, anelastic)
• Geometry is important (sphericity)
• Operate in nonlinear regime
• Resolution issues. Smallest resolvable scales are
– in the inertial range
– rotationally constrained
– stratified
Need sophisticated sub-grid models
Chicago 2003
Modeling: small-scale generation
cold
g
•
Plane parallel layer of fluid
•
Boussinesq approximation
•
Ra=500,000; P=1; Pm=5
time evolution
Simulations by Lenz & Cattaneo
hot
temperature
Chicago 2003
Modeling: physical parameters
Rm 
103
102

Pm=1

simulations

Liquid metal experiments
103
107
Re
• Dynamo must operate in the inertial range of the turbulence
• Driving velocity is rough
• How do we model MHD behaviour with Pm <<1
Chicago 2003
Modeling: kinematic and dynamical issues
Re=550, Rm=550
yes
• Does the dynamo still operate?
(kinematic issue)
• Dynamo may operate but become
extremely inefficient (dynamical
issue)
Re=1100, Rm=550
no
Pm=1
Pm=0.5
Chicago 2003
Modeling: magneto-convection
• Relax requirement that magnetic field be self sustaining (i.e.
impose a uniform vertical field)
• Construct sequence of simulations with externally imposed
field, 8 ≥ Pm ≥ 1/8, and S =  = 0.25
• Adjust Ra so that Rm remains “constant”
Pm
8.0
4.0
2.0
1.0
0.5
0.25
0.125
Ra
9.20E+04
1.40E+05
2.00E+05
3.50E+05
7.04E+05
1.40E+06
2.80E+06
Nx, Ny
256
256
256
512
512
512
768
Simulations by Emonet & Cattaneo
Chicago 2003
Modeling: magneto-convection
B-field (vertical)
vorticity (vertical)
Pm = 8.0
Pm = 0.125
Chicago 2003
Modeling: magneto-convection
•
Energy ratio flattens out for Pm < 1
•
PDF’s possibly accumulate for Pm < 1
•
Evidence of regime change in cumulative
PDF across Pm=1
•
Possible emergence of Pm independent
regime
Chicago 2003
Summary
Two related but distinct dynamo problems.
• Large-scale dynamo
– Reproduce cyclic activity
– Reproduce migration pattern
– Reproduce angular momentum distribution (CV and tachocline)
– Needs substantial advances in computational capabilities
• Small scale dynamo
– Non helical generation
– Small Pm  turbulent dynamo