* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Document
Nuclear structure wikipedia , lookup
Hunting oscillation wikipedia , lookup
Relativistic mechanics wikipedia , lookup
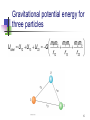
Internal energy wikipedia , lookup
Grand canonical ensemble wikipedia , lookup
Gibbs free energy wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
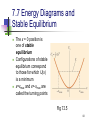
Thermodynamic system wikipedia , lookup
Heat transfer physics wikipedia , lookup
Eigenstate thermalization hypothesis wikipedia , lookup
7.4 Conservative Forces and Potential Energy Define a potential energy function, U, such that the work done by a conservative force equals the decrease in the potential energy of the system The work done by such a force, F, is DU is negative when F and x are in the same direction 1 Conservative Forces and Potential Energy The conservative force is related to the potential energy function through The conservative force acting between parts of a system equals the negative of the derivative of the potential energy associated with that system This can be extended to three dimensions 2 Conservative Forces and Potential Energy – Check Look at the case of an object located some distance y above some reference point: This is the expression for the vertical component of the gravitational force 3 7.6 Potential Energy for Gravitational Forces Generalizing gravitational potential energy uses Newton’s Law of Universal Gravitation: The potential energy then is Fig 7.12 4 Potential Energy for Gravitational Forces, Final The result for the earth-object system can be extended to any two objects: 5 Gravitational potential energy for three particles 6 Electric Potential Energy Coulomb’s Law gives the electrostatic force between two particles This gives an electric potential energy function of 7 8 9 7.7 Energy Diagrams and Stable Equilibrium The x = 0 position is one of stable equilibrium Configurations of stable equilibrium correspond to those for which U(x) is a minimum x=xmax and x=-xmax are called the turning points Fig 7.15 10 Energy Diagrams and Unstable Equilibrium Fx = 0 at x = 0, so the particle is in equilibrium For any other value of x, the particle moves away from the equilibrium position This is an example of unstable equilibrium Configurations of unstable equilibrium correspond to those for which U(x) is a maximum Fig 7.16 11 A particle is attached between two identical springs on a horizontal frictionless table. Both springs have spring constant k and are initially unstressed. (a) The particle is pulled a distance x along a direction perpendicular to the initial configuration of the springs as shown in Figure. Show that the force exerted by the springs on the particle is L F 2 kx 1 x 2 L2 ˆ i (b) Determine the amount of work done by this force in moving the particle from x = A to x = 0. 12 (a) Show that the potential energy of the system is Ux kx2 2kL L x 2 L2 (b) Make a plot of U(x) versus x and identify all equilibrium points. (c) If the particle of mass m is pulled in a distance d to the right and then released, what is its speed when it reaches the equilibrium point x = 0? 13 Exercises of chapter 7 3, 5, 9, 14, 17, 26, 33, 39, 42, 54, 62 14