* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download GRAVITATIONAL POTENTIAL ENERGY
Newton's laws of motion wikipedia , lookup
Classical mechanics wikipedia , lookup
Newton's theorem of revolving orbits wikipedia , lookup
Hooke's law wikipedia , lookup
Relativistic mechanics wikipedia , lookup
Matter wave wikipedia , lookup
Heat transfer physics wikipedia , lookup
Internal energy wikipedia , lookup
Gibbs free energy wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
Centripetal force wikipedia , lookup
Hunting oscillation wikipedia , lookup
Eigenstate thermalization hypothesis wikipedia , lookup
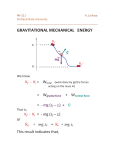
PH-211 Portland State University A. La Rosa ______________________________________________________ For some forces it is possible to associate a corresponding potential energy (friction forces do not qualify). Next we show why the gravitational force qualifies. GRAVITATIONAL POTENTIAL ENERGY zi Ki m N mg Kf zf We know Kf - Ki = Wtotal (work done by all the forces acting on the mass m) = Wgravity-force + Wnormal-force = - mg (zf – zi) + 0 That is, Kf - Ki = - mg (zf – zi) or Kf + mg zf = Ki + mg zi This result indicates that the quantity page - 2 K + mgz remains constant throughout the motion. Such a constant quantity is called the "gravitational mechanical energy E" of the system E = gravitational mechanical energy K Kinetic energy + mgz It is called gravitational potential energy In terms of this definition, our previous result indicates that That is, the gravitational mechanical energy of the system remains constant throughout the motion page - 3 Z E (at A) = E( at B) = E (at C) What we have just learned is: If we know the gravitational mechanical energy of the particle at just one point of its trajectory Then we know its mechanical energy everywhere at any other point of its trajectory Example. Rank the plums according to their speed when they reach the upper level Z v3 v2 v1 v v Each plum is launched from the same bottom level and with the same speed E = Ki + Ui = Kf + Uf (1/2) mv2 + 0 = (1/2) mv12 + mgh (1/2) mv2 + 0 = (1/2) mv22 + mgh (1/2) mv2 + 0 = (1/2) mv32 + mgh Bottom level z=0 This implies v1 = v2 = v3 Upper level z=h page - 4 Example. Three blocks start their motion with zero velocity at level zB. page - 5 B v3 Draw the vector velocity at the level A in each case In which case is the speed at the level A greater? Conservation of mechanical energy implies, A page - 6 Conservation of mechanical energy implies, Conservation of mechanical energy implies, From Work done by a SPRING FORCE page - 7 Frequently (but no always), the spring's equilibrium position (where the spring is neither elongated or compressed) is taken as the coordinate x=0. Spring neither stretched nor compressed 0 Stretched spring F 0 Notice the opposite direction between F and x Compressed spring 0 Spring constant [N / m] This expression assumes the spring's equilibrium position (where the spring is neither elongated or compressed) is taken as the coordinate x=0. Expression valid provided we do not stretch the spring "too much" Frequently, the spring's equilibrium position (where the spring is neither page - 8 elongated or compressed) is taken as the coordinate x=0. This gives F(x)= -k x Otherwise, if the equilibrium position were chose at x= xo, then F(x) = -k (x- xo) X Equilibrium position Calculation of the work done by a spring force 0 x=0 Equilibrium position X page - 9 page - 10 Work done by the spring force on the block when it moves from x=xi to x=xf . At x=0 the spring is neither stretched or compressed Similar to the gravitational force, the work done by the spring force depends only on the final and initial position. Notice, page - 11 v 0 i f f i v i 0 0 f f i Notice, The result implies that the work done on the block by a spring force in a round trip is zero. (Forces with this property are called CONSERVATIVE). Now we show that the spring force can also be associated with a corresponding potential energy. Lets's apply our general result, page - 12 page - 13 This result suggest to define a spring mechanical energy as follows, Spring potential energy Spring mechanical energy Smaller + bigger = const = Eo Bigger smaller = const = Eo + K U= X page - 14 Exercise: Question #8 , Chapter 7, (page 159) page - 15 page - 16 Formal definition of POTENTIAL ENERGY (valid for conservative forces only; i. e. forces for which the work along a trip is independent of the particular trajectory. ) Consider a specific conservative force F We know the value of F at each coordinate (x, y, z) Definition of 'Potential energy difference" UB - UA= = - page - 17 For PH-211 A. La Rosa Portland State University ______________________________________________________ Potential Energy and Conservative Forces & For a given conservative force F , a scalar potential energy U is associated to such a force. & F Vector l U (1) Scalar Such an association is built through the definition of the “potential energy difference UB - UA ” as the negative value of & the work W done by the conservative force F (when taking the particle from an initial potion A to a final position B), & B) UB - UA ≡ - W (A o F (2) By making the point B a general position x, and the point A a reference fixed position, then one obtains the potential energy U as a function of x, (3) UX - Uref point ≡ - W (Ref point Æ X) UX - Uref point ≡ - W (Ref point Æ X) Alternative notation, U(x) = Uref point - W (Ref point Æ X) (4) (We will see below why it is convenient to put the minus sign in the definition above) Examples x In the case of the spring force, for example, we found in the previous pages of these notes that, W (A Æ B) = - (1/2) k [ (xB)2 - (xA)2 ] (5) xA xB 0 Hence, the expression UB - UA ≡ - W (A Æ B) implies UB - UA ≡ + (1/2) k [ ( xB)2 - (xA)2 ] If we take as a reference point A the origin (x=0), and make B a general point of coordinate x, then we obtain, U(x) = U(0) + (1/2) k x2 (6) Arbitrarily we assign, U(0) = 0 which makes (6) to become, U(x) = (1/2) k x2 In short & F F = - kx (7) l l U 2 U(x) = (1/2) k x (8) x Similarly, in the case of the gravitational force. Previously we found, W (A Æ B) = - mg [ zB - zA ] (9) a value that is independent of the particular trajectory followed by the object during its motion from A to B. zB B g m zA A Accordingly, the expression UB - UA ≡ - W (A Æ B) implies UB - UA ≡ + mg ( zB - zA ) (10) This quantity depends only on the initial and final positions of the particle If we take as a reference point A a point of coordinate z0, and make B a general point of coordinate z, then we obtain, U(z) = U(0) + mg ( z - zo ) Arbitrarily we assign, U(0) = U0 which makes (11) to become, (11) U(z) = U0 + mg ( z - zo ) In short & F & F l (12) U (13) = - mg ẑ l U(z) = U0 + mg ( z - zo ) In the definition of the potential energy UB - UA ≡ - W (A Æ B) , the negative sign in front of W is quite convenient for expressing the conservation of the mechanical energy. In effect, as we know, from the work / kinetic-energy theorem we have W (A Æ B) = KB - KA Combining this result with the definition UB - UA ≡ - W (A Æ B) one obtains, UB - UA ≡ - W (A Æ B) = - ( KB - KA ) which leads to KB + UB = KA + UA = const (14) [ Notice, had we chosen VB - VA ≡ + W (A Æ B) we would have ended up with something like KB - VB = KA - VA ] K + U = E is defined as the mechanical energy of the particle Since A and B are two arbitrary points along the trajectory of the particle, the result in the previous page indicates that the mechanical energy conserves thought the motion lternative definition of the Potential Energy In the previous section we defined a potential difference UB - UA & in terms of the work done by the conservative force F , & UB - UA ≡ - W (A o B) . We will offer an alternative, but F equivalent, definition in terms of an external force. B F Conservative force m A & The graph above shows the force lines of a conservative force F . Let’s assume that the particle of mass m moves from A to B along the indicated trajectory. As we know, the particle will pick up some kinetic energy, and some potential energy along the way. Question: What does an external agent will have to do in order to move the particle from A to B, along the same trajectory, but at constant velocity (velocity ~ 0)? Motion at constant velocity implies equilibrium. It means that the external force will have to be of the same magnitude of the conservative force, but pointing in opposite direction. That is, & F external & F (15) z B Fext F Conservative Fext m force X A Fext = - F Then & UB - UA ≡ - W (A o B) F & o B) = Wext (A F ext That is UB - UA ≡ & o B) Wext (A F ext (16) Work done by the external force to take the particle from A to B at constant speed The definitions (2) and (16) should provide the potential-energy difference between the points A and B.