Download GRAVITATIONAL POTENTIAL ENERGY

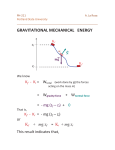
PH-211
Portland State University
A. La Rosa
______________________________________________________
For some forces it is possible to associate a corresponding
potential energy (friction forces do not qualify).
Next we show why the gravitational force qualifies.
GRAVITATIONAL POTENTIAL ENERGY
zi
Ki
m
N
mg
Kf
zf
We know
Kf - Ki = Wtotal (work done by all the forces
acting on the mass m)
= Wgravity-force
+ Wnormal-force
= - mg (zf – zi) + 0
That is,
Kf - Ki = - mg (zf – zi)
or
Kf + mg zf = Ki + mg zi
This result indicates that the quantity
page - 2
K + mgz
remains constant throughout the motion.
Such a constant quantity is called the "gravitational
mechanical energy E" of the system
E =
gravitational
mechanical
energy
K
Kinetic
energy
+ mgz
It is called
gravitational
potential energy
In terms of this definition, our previous result indicates that
That is,
the gravitational mechanical energy of the system
remains constant throughout the motion
page - 3
Z
E (at A) = E( at B) = E (at C)
What we have just learned is:
If we know the gravitational mechanical energy
of the particle at just one point of its trajectory
Then
we know its mechanical energy everywhere at
any other point of its trajectory
Example. Rank the plums according to their speed when they
reach the upper level
Z
v3
v2
v1
v
v
Each plum is launched from the same
bottom level and with the same
speed
E
=
Ki
+ Ui
=
Kf
+
Uf
(1/2) mv2 + 0
=
(1/2) mv12 +
mgh
(1/2) mv2 + 0
=
(1/2) mv22 +
mgh
(1/2) mv2 + 0
=
(1/2) mv32 +
mgh
Bottom level
z=0
This implies v1 = v2 = v3
Upper level
z=h
page - 4
Example. Three blocks start their motion with zero
velocity at level zB.
page - 5
B
v3
Draw the vector velocity at the level A in each case
In which case is the speed at the level A greater?
Conservation of mechanical energy implies,
A
page - 6
Conservation of mechanical energy implies,
Conservation of mechanical energy implies,
From
Work done by a SPRING FORCE
page - 7
Frequently (but no always), the spring's equilibrium position (where the spring is
neither elongated or compressed) is taken as the coordinate x=0.
Spring neither stretched
nor compressed
0
Stretched
spring
F
0
Notice the opposite direction
between F and x
Compressed
spring
0
Spring constant
[N / m]
This expression assumes the
spring's equilibrium position
(where the spring is neither
elongated or compressed) is
taken as the coordinate x=0.
Expression valid provided we do not stretch the spring "too much"
Frequently, the spring's equilibrium
position (where the spring is neither
page - 8
elongated or compressed) is taken as the
coordinate x=0. This gives F(x)= -k x
Otherwise, if the equilibrium position
were chose at x= xo, then F(x) = -k (x- xo)
X
Equilibrium
position
Calculation of the work done
by a spring force
0
x=0
Equilibrium
position
X
page - 9
page - 10
Work done by the
spring force on the
block when it moves
from x=xi to x=xf .
At x=0 the spring
is neither stretched
or compressed
Similar to the gravitational force, the work done by the spring force
depends only on the final and initial position.
Notice,
page - 11
v
0
i
f
f
i
v
i
0
0
f
f
i
Notice,
The result
implies that the work done on the block by a spring
force in a round trip is zero.
(Forces with this property are called CONSERVATIVE).
Now we show that the spring force can also be associated
with a corresponding potential energy.
Lets's apply our general result,
page - 12
page - 13
This result suggest to define a spring mechanical energy as
follows,
Spring
potential
energy
Spring
mechanical
energy
Smaller +
bigger
= const = Eo
Bigger
smaller
= const = Eo
+
K
U=
X
page - 14
Exercise: Question #8 , Chapter 7, (page 159)
page - 15
page - 16
Formal definition of POTENTIAL ENERGY
(valid for conservative forces only; i. e. forces for which the work
along a trip is independent of the particular trajectory. )
Consider a specific conservative force F
We know the
value of F at
each coordinate
(x, y, z)
Definition of 'Potential energy
difference"
UB - UA= = -
page - 17
For
PH-211
A. La Rosa
Portland State University
______________________________________________________
Potential Energy and Conservative Forces
&
For a given conservative force F , a scalar potential energy U is
associated to such a force.
&
F
Vector
l
U
(1)
Scalar
Such an association is built through the definition of the
“potential energy difference UB - UA ” as the negative value of
&
the work W done by the conservative force F (when taking the
particle from an initial potion A to a final position B),
&
B)
UB - UA ≡ - W (A o
F
(2)
By making the point B a general position x, and the point A a
reference fixed position, then one obtains the potential energy U
as a function of x,
(3)
UX - Uref point ≡ - W (Ref point Æ X)
UX - Uref point ≡ - W (Ref point Æ X)
Alternative notation,
U(x) = Uref point - W (Ref point Æ X)
(4)
(We will see below why it is convenient to put the minus
sign in the definition above)
Examples
x In the case of the spring force, for example, we found in the
previous pages of these notes that,
W (A Æ B) = - (1/2) k [ (xB)2 - (xA)2 ]
(5)
xA
xB
0
Hence, the expression UB - UA ≡ - W (A Æ B) implies
UB - UA ≡ + (1/2) k [ ( xB)2 - (xA)2 ]
If we take as a reference point A the origin (x=0), and make B a
general point of coordinate x, then we obtain,
U(x) = U(0) + (1/2) k x2
(6)
Arbitrarily we assign,
U(0) = 0
which makes (6) to become,
U(x) = (1/2) k x2
In short
&
F
F = - kx
(7)
l
l
U
2
U(x) = (1/2) k x
(8)
x Similarly, in the case of the gravitational force. Previously we
found,
W (A Æ B) = - mg [ zB - zA ]
(9)
a value that is independent of the particular trajectory followed
by the object during its motion from A to B.
zB
B
g
m
zA
A
Accordingly, the expression UB - UA ≡ - W (A Æ B) implies
UB - UA ≡ + mg ( zB - zA )
(10)
This quantity depends only on the
initial and final positions of the
particle
If we take as a reference point A a point of coordinate z0, and
make B a general point of coordinate z, then we obtain,
U(z) = U(0) + mg ( z - zo )
Arbitrarily we assign,
U(0) = U0
which makes (11) to become,
(11)
U(z) = U0 + mg ( z - zo )
In short
&
F
&
F
l
(12)
U
(13)
= - mg ẑ
l
U(z) = U0 + mg ( z - zo )
In the definition of the potential energy UB - UA ≡ - W (A Æ B) ,
the negative sign in front of W is quite convenient for expressing
the conservation of the mechanical energy. In effect, as we know,
from the work / kinetic-energy theorem we have
W (A Æ B) = KB - KA
Combining this result with the definition UB - UA ≡ - W (A Æ B)
one obtains,
UB - UA ≡ - W (A Æ B) = - ( KB - KA )
which leads to
KB + UB = KA + UA = const
(14)
[ Notice, had we chosen VB - VA ≡ + W (A Æ B) we would have
ended up with something like KB - VB = KA - VA ]
K + U = E is defined as the mechanical energy of the particle
Since A and B are two arbitrary points along the trajectory of the
particle, the result in the previous page indicates that the
mechanical energy conserves thought the motion
lternative definition of the Potential Energy
In the previous section we defined a potential difference UB - UA
&
in terms of the work done by the conservative force F ,
&
UB - UA ≡ - W (A o
B) . We will offer an alternative, but
F
equivalent, definition in terms of an external force.
B
F Conservative
force
m
A
&
The graph above shows the force lines of a conservative force F .
Let’s assume that the particle of mass m moves from A to B along
the indicated trajectory. As we know, the particle will pick up
some kinetic energy, and some potential energy along the way.
Question: What does an external agent will have to do in order to
move the particle from A to B, along the same
trajectory, but at constant velocity (velocity ~ 0)?
Motion at constant velocity implies equilibrium. It means that the
external force will have to be of the same magnitude of the
conservative force, but pointing in opposite direction. That is,
&
F external
&
F
(15)
z
B
Fext
F Conservative
Fext
m
force
X
A
Fext = - F
Then
&
UB - UA ≡ - W (A o
B)
F
& o B)
= Wext (A 
F
ext
That is
UB - UA ≡
& o B)
Wext (A 
F
ext
(16)
Work done by the external force
to take the particle from A to B at
constant speed
The definitions (2) and (16) should provide the potential-energy
difference between the points A and B.