* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download A Brief History of Planetary Science
Newton's laws of motion wikipedia , lookup
Centripetal force wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
Equations of motion wikipedia , lookup
Eigenstate thermalization hypothesis wikipedia , lookup
Internal energy wikipedia , lookup
Classical central-force problem wikipedia , lookup
Kinetic energy wikipedia , lookup
Hunting oscillation wikipedia , lookup
Relativistic mechanics wikipedia , lookup
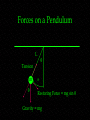
Pendulums Physics 202 Professor Lee Carkner Lecture 4 “The sweep of the pendulum had increased … As a natural consequence its velocity was also much greater.” --Edgar Allan Poe, “The Pit and the Pendulum” PAL #3 SHM Equation of motion for SHM, pulled 10m from rest, takes 2 seconds to get back to rest w= 2p/T = 0.79 How long to get ½ back arccos(5/10)/0.79 = t =1.3 seconds PAL #3 SHM (cont.) Max speed v = -wxm sin(wt) v max when sin =1 Where is max v? Max acceleration a = -w2xm cos(wt) Where is max a? The ends (max force from spring) Simple Harmonic Motion For motion with period = T and angular frequency = w = 2p/T: v=-wxmsin(wt + f) The force is represented as: where k=spring constant= mw2 SHM and Energy A linear oscillator has a total energy E, which is the sum of the potential and kinetic energies (E=U+K) As one goes up the other goes down SHM Energy Conservation Potential Energy 2 1 UFdxkxdx kx 2 From our expression for x U=½kxm2cos2(wt+f) Kinetic Energy K=½mv2 = ½mw2xm2 sin2(wt+f) K = ½kxm2 sin2(wt+f) The total energy E=U+K which will give: E= ½kxm2 Types of SHM Every system of SHM needs a mass to store kinetic energy and something to store the potential energy (to provide the springiness) There are three types of systems that we will discuss: Each system has an equivalent for k Pendulums A mass suspended from a string and set swinging will oscillate with SHM Consider a simple pendulum of mass m and length L displaced an angle q from the vertical, which moves it a linear distance s from the equilibrium point Pendulum Forces Forces on a Pendulum L q Tension m q s Restoring Force = mg sin q Gravity = mg The Period of a Pendulum The the restoring force is: F = -mg sin q We can replace q with s/L Compare to Hooke’s law F=-kx Period for SHM is T = 2p (m/k)½ T=2p(L/g)½ Pendulum and Gravity The period of a pendulum depends only on the length and g, not on mass A pendulum is a common method of finding the local value of g The Pendulum Clock Invented in 1656 by Christiaan Huygens, the pendulum clock was the first timekeeping device to achieve an accuracy of 1 minute per day. Application of a Pendulum: Clocks Since a pendulum has a regular period it can be used to move a clock hand Consider a clock second hand attached to a gear The gear is stopped by a toothed mechanism attached to a pendulum of period = 2 seconds Since the period is 2 seconds the second hand advances once per second Physical Pendulum Properties of a physical pendulum depend on its moment of inertia (I) and the distance between the pivot point and the center of mass (h), specifically: T=2p(I/mgh)½ Non-Simple Pendulum Torsion Pendulum Torsion Pendulum If the disk is twisted a torque is exerted to move it back due to the torsion in the wire: tkq We can use this to derive the expression for the period: T=2p(I/k)½