Download x - UniMAP Portal

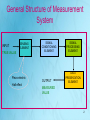
Sensors and Measurements
Penderia & Pengukuran
ENT 164
Piezoelectric Sensors
Hema C.R.
School of Mechatronics Engineering
Northern Malaysia University College of Engineering
Perlis , Malaysia
Contact no: 04 9798442
Email: [email protected]
1
General Structure of Measurement
System
SENSING
ELEMENT
INPUT
TRUE VALUE
Piezo-electric
Hall effect
SIGNAL
CONDITIONING
ELEMENT
OUTPUT
SIGNAL
PROCESSING
ELEMENT
DATA
PRESENTATION
ELEMENT
MEASURED
VALUE
2
Sensing Elements
Resistive
silicon
temperature & strain
Capacitive
Pressure, level ,strain & humidity
Inductive
strain
pressure
temperature
Thermo Electric
temperature
Piezoelectric
O2
vibration , force & acceleration
Electro Chemical
gas composition & ionic concentration
Flow
Hall Effect Sensor
Magnetic field
3
Piezoelectric Sensing
Elements
4
The word piezo is derived from the Greek piezein,
which means to squeeze or press.
The effect known as piezoelectricity was discovered
by brothers Pierre and Jacques Curie in 1880.
Crystals which acquire a charge when compressed,
twisted or distorted are said to be piezoelectric.
Piezoelectric materials also show the opposite effect,
called converse piezoelectricity, where the application
of an electrical field creates mechanical deformation in
the crystal.
5
Further Reading : Crystal classes & Piezoelectric crystal classes
Crystals
Crystals are naturally occurring material
that can be induced to resonate or
vibrate at an exact frequency.
Crystals are anisotropic materials
physical properties depend on the direction
Quartz, a piezoelectric crystal that
provides excellent mechanical and
electrical stability, acquires a charge
when compressed, twisted, or distorted.
Quartz crystals are used as active
elements in oscillators
A Quartz "Crystal"
Isotropic materials have same physical properties in all directions
6
Piezoelectric Materials
Quartz (SiO2)
Barium Titanate (BaTiO3)
Gallium Orthophosphate (GaPO4),
Polymer materials like rubber, wool, wood
and silk exhibit piezoelectricity to some
extent
Applications
Microphones, guitars, sonar, motors
microbalances, clocks and vibration
sensors.
7
Piezoelectric Effect
8
When force is applied to a crystal , the crystal
atoms are displaced from their normal
positions
Displacement x is proportional to applied
force F
1
x F
k
(1)
where k is the stiffness in the order of 2 109 Nm1
The displacement can be summarised using
a transfer function
9
Transfer Function of an Element
When input signal of an element is changed suddenly the
output signal will not change instantaneously. The way in which
an element responds to sudden input changes are termed its
dynamic characteristics, which can be conveniently summarised
using a transfer function

Element Transfer Function: G s  

f 0 s 

f i s 

f 0 s   G s  f i s 
Transfer function of an output signal is the product of
element transfer function and transfer function of the input
signal
10
Transfer Function Of Second Order
Elements
Sensor converts force into
displacement , diagram
shows
the
conceptual
model which has a mass m
kg, a spring of stiffness k
N/m
and
a
damper
constant  Ns/m.
The system is initially at
rest at time t =0so that the

initial velocity x0    0 and
the
initial acceleration

x 0    0 . The initial input
force F(0-) is balanced by
the spring force at the initial
displacement x(0-)
kx
Spring k
F
Mass
m
Damper 
.

x
kx
x=0
Model of an Elastic force sensor
an analogous system to a piezo
force sensor
11
F (0)  kx(0)
(i)
If input force is suddenly increased at t = 0, then element is
no longer in a steady state and its dynamic behavior is
described by Newton ‘s second law
resultant force = mass x acceleration


F  kx   x  m x
(ii)
and


m x   x  kx  F
Defining F and
x to be deviations in F and x
12
F  F  F (0), x  x  x(0)



(iii)

 x  x,  x  x
The differential equation




m x   x  kx  F
now becomes
m x   x  kx(0)  kx  F (0)  F
Which using equation (i) reduces to


m x   x  kx  F
i.e
m d 2 x  dx
1

 x  F
2
k dt
k dt
k
(iv)
Second-order Linear Differential Equation
13
If we define
k
Undamped natural frequency n 
m
and
Damping ratio
then

rad /s

2 km
m / k  1 / n2 ,  / k  2 / n
(v)
Eqn.(iv) can be expressed in standard form
1 d x 2 dx
1

 x  F
2
2
n dt
n dt
k
2
(xi )

(vi)
Second-order Linear Differential Equation
14
d
f (t )  sf ( s )  f (0)
dt
d2
2
f
(
t
)

s
f ( s )  sf (0)  f (0)
2
dt
Laplace Transform of
Time functions f(t)
To find transfer function of the element we use Laplace
transform of equation (vi)



1 2 
2
[ s  x ( s)  sx(0)   x(0)]  [ s x ( s)  x(0)]   x ( s)
2
n
n
1 
  F (s)
k
(vii)

Since

 x ( 0 )  x (0 )  0
and
 x ( 0 )  0
Equation (vii) reduces to
15
 1 2 2
 
1 
s  1  x ( s)   F ( s)
 2s 
n
k
 n

(viii)
Thus

 x(s)

 F ( s)

1
G(s)
k
Where 1/k =steady-state sensitivity K
1
G( s) 
 1 2 2

  2 s   s  1
n
 n

(ix)
Transfer Function for a second–order element
16
Transfer Function of a Piezoelectric Element
Using transfer function for a second order element
G( s ) 
1
1 2 2
s 
s 1
2
n
n
x and F can be represented by the second order transfer function
1
x
k
(s)
1
2
F
( s )
s 1
2
n
n
Where natural frequency   2f
n
n
f n = 10 to 100 kHz

(2)
is large
and damping ratio
= 0.01
17
Further Reading : Page 56 - Bentley
This deformation of crystal lattice results in crystal
acquiring a charge q , proportional to x
q = Kx
(3)
From equation (1) and (3) we get
K
q
F  dF
k
(4)
Direct Piezoelectric Effect
K
CN 1 is the charge sensitivity to force
where d 
k
18
A piezoelectric crystal gives a direct electrical output,
proportional to applied force, so that a secondary
displacement sensor is not required.
Piezoelectric crystals also produce an inverse effect
where an voltage applied to the crystal causes a
mechanical displacement.
x  dV
(5)
Inverse Piezoelectric Effect
inverse effect is used in ultrasonic transmitters
CN 1 is identical with mV 1
19
Measuring ‘q’
Metal electrodes are deposited on opposite
faces of the crystal to form a capacitor to
measure the charge q
t
Piezoelectric
crystal
Metal Plate
Capacitance of the parallel plate capacitor
formed
 0A
(6)
CN 

t
0

Further Reading : Page 160 - Bentley
Permittivity of free space (vacuum)
Relative permittivity or dielectric constant of
the insulating material (here the piezo )
A Area of plate
20
The crystal can be represented as charge
generator q in parallel with a capacitance
C N or a Norton equivalent circuit
consisting of current source iN in parallel
with C N .
Magnitude of iN is
dq
dx
iN 
K
dt
dt
(7)
21
Further Reading : Page 82 - Bentley
transfer function form of iN
iN
( s )  Ks
x
where d/dt is replaced by the Laplace operator
For steady force
(8)
s
F,
F and x are constant with time
Such that dx/dt and iN are zero.
22
Further Reading: http://en.wikipedia.org/wiki/Laplace_transform#Formal_definition
Piezoelectric Force
Measurement System
23
Circuit of a force measurement system
iN
Piezoelectric
Crystal
CN
CC
Capacitive
Cable
RL V
L
Figure 1.
Piezoelectric Force
measurement system
Recorder
Consider a piezoelectric crystal connected to a
recorder where
RL is a pure resistive load
CC is pure capacitance of the cable
VL is the recorder voltage
24
Transfer function relating to VL and
iN
is
VL ( s )
RL

iN ( s ) 1  RL C N  CC s
(9)
Overall system transfer function relating
recorder voltage VL to input force F is
VL
VL iN  x
s  
F
i N  x  F
(10)
25
Further Reading : Page 84 - Bentley
1
x
k
(s)
1
2
F
(
s
)

s 1
n2
n
From equation (2),(8) and (9) we get
1
VL
RL
k
s  
Ks
1 2 2
1  RL C N  CC s
F
s 
s 1
2
iN
( s )  Ks
x
VL ( s )
RL

iN ( s ) 1  RL C N  CC s
n
n
RL C N  CC s
K
1
1

k C N  CC  1  RL C N  CC s 1 s 2  2 s  1
2
n
n
VL
d
s
1
s  
C N  CC  1  s   1 2 2 
F
  2 s   s  1
n
 n

(11)
Transfer Function for basic Piezoelectric force measurement system
where
  RL CN  CC 
(Tau )

26
Disadvantages of the basic piezoelectric system
1.Steady state sensitivity is equal to d / CN  CC . Thus
the system sensitivity depends on the cable
capacitance CC i.e. length and type of cable.
2.The dynamic part of the system transfer function is
(ignoring recorder dynamics)
s
1
G( s) 
s  1  1 2 2 
  2 s   s  1
n
 n

(12)
The second term is characteristic of all elastic
elements and cannot be avoided , however it causes
no problem if the highest signal frequency MAX is
well below  n
(Tau )

27
The first term s / s  1indicates that system cannot be used
for measuring d.c. and slow varying forces.
Illustration
Consider a frequency response
characteristics plot for G j  and arg G j 
of a typical measurement system
iN
Piezoelectric
Crystal
CN
CC
Capacitive
Cable
RL V
L
Figure 1.
Piezoelectric Force
measurement system
Recorder
28
Amplitude Ratio G  j  

1 
2
1
2
  
2 
1


4

 2 
n2
n 

2
(13)
2
 


2

   
n

0
1
1

Phase difference arg G  j   90  tan    tan 
1    2  
  n2  


Figure 2: Approximate
Frequency Response
Characteristics
Piezoelectric
Measurement System
with charge amplifier
29
s
The s  1 term causes a low frequency
roll-off so that G j   0
at
  0 and
system cannot be used for frequencies much
below 1

These disadvantages can be overcome by
introducing a charge amplifier into the
system as shown in Figure 2
30
This system gives an output proportional to  iN dt
i.e. an output proportional to charge q .
Since iN  dq
the system gives a non zero
dt
output for steady force input. From Figure 3 we
Have
i1  iF  i
(14)
and charge on feedback capacitor C F is
qF  CF V  VOUT 
(15)
For an ideal operational amplifier we have
i  i  0 and V  V
In this case we have V  V  0 and iF  dqF dt
so that
i1  iF 
dqF
dVOUT
 C F
dt
dt
(16)
31
Since the potential drop across
C N and CC is zero
dq
i1  iN 
dt
(17)
From equation (16) and (17) we have
dVOUT
1 dq

dt
CF dt
i.e.
VOUT
q

CF
(18)
Transfer Characteristic Of Ideal Charge Amplifier
From equation (18), (3) and (2) the overall transfer function for
force measurement system is
V OUT
d
1
( s) 
C F  1 2 2

F
  2 s   s  1
n
 2

Transfer Function for Piezoelectric system with Ideal Charge Amplifier
(19)
32
The steady state sensitivity is now d C
i.e. it
F
depends only on the capacitance CF of the
charge amplifier and is independent of
transducer and cable capacitance
Common Piezoelectric materials
Quartz
Lead zirconium titanate (PZT)
Barium titanate (BaTi2O3)
PolyVinylidine DiFluoride (PVDT)
33
Piezoresistive Sensing
Elements
34
Piezoresistivity is defined as the change in resistivity 
of a material with applied mechanical strain e and
is represented by the term 1e    in the equation (20)
 




1
G  1  2v 

e  
(20)
Gauge factor of Strain gauge
v is Poisson’s Ratio
Silicon doped with small amounts of n type or p type
materials exhibits a large piezoresistive effect and is
used to manufacture strain gauges.
35
Further Reading : Page 158 - Bentley
Poisson’s Ratio
When a sample of material is stretched in
one direction, it tends to get thinner in the
other two directions. Poisson's ratio (v) is a
measure of this tendency. It is defined as
the ratio of the strain in the direction of the
applied load to the strain normal to the
load. For a perfectly incompressible
material, the Poisson's ratio would be
exactly 0.5. Most practical engineering
materials have v between 0.0 and 0.5..
36
Reference
1. ‘Principles of Measurement Systems’ by John P
Bentley. [Text book]
2. http://www.resonancepub.com/piezoele.htm
3. http://hyperphysics.phyastr.gsu.edu/hbase/solids/piezo.html
4. ‘Piezoelectric Transducers and Applications’ by
Antonio Arnau
37