* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Lecture9 (Motion)
Fictitious force wikipedia , lookup
Newton's theorem of revolving orbits wikipedia , lookup
Nuclear force wikipedia , lookup
Centrifugal force wikipedia , lookup
Virtual work wikipedia , lookup
Fundamental interaction wikipedia , lookup
Centripetal force wikipedia , lookup
Newton's laws of motion wikipedia , lookup
Engineering
Fundamentals
Session 9
Equilibrium
• A body is in Equilibrium if it moves with
constant velocity. A body at rest is a special
case of constant velocity i.e. v = 0 = constant.
• For a body to be in Equilibrium the resultant
force (meaning the vector addition of all the
forces) acting on the body must be zero.
• Resulting force = vector addition of force
vectors
• A Force can be defined as 'that which tends
to cause a particle to accelerate‘.
Equilibrium of Concurrent
F1
Forces
Equilibrant E
Equilibrant E
Force
F2
Resultant R
Equilibrant E are equal and
opposite to Resultant R
R
Fy
E
F2
F1
E = -R
Fx
Particle Vs Rigid Body
• A particle has dimension = 0
• A Rigid body is a non-particle body
and it does not deform (change
shape).
Concurrent forces:
Coplanar
forces: all
forces lie on
the same plane
all forces acting a
the same point
Conditions for Equilibrium
i=n
F 0
i
i =1
Explanation:
Sum of forces = 0,
Or
F1 + F2 + … + Fn = 0
Example
F1 + F2 + F3= 0
Conditions for Equilibrium
• Breaking down into x and y
components
i=n
F
x, i
i =1
i=n
0; and Fy, i 0;
Example: For
three forces
acting on a
particle
i =1
Fx,1 Fx,2 Fx,3 0;
Fy,1 Fy,2 Fy,3 0;
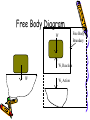
Free Body Diagram
• Free body diagram isolates a rigid
body to describe the system of
forces acting on it.
R
R
R
mg
R
Free Body Diagram
Free Body
W
Boundary
Wr Reaction
W
Wa Action
Definitions
• System of Particles or Bodies
Two or more bodies or particles connected
together are referred to as a system of bodies or
particles.
• External Force
External forces are all the forces acting on a
body defined as a free body or free system of
bodies, including the actions due to other bodies
and the reactions due to supports.
Transmissibility of Force
F
F
F
Load and Reaction
• Loads are forces that are applied to
bodies or systems of bodies.
• Reactions at points supporting bodies
are a consequence of the loads
applied to a body and the equilibrium
of a body.
Tensile and Compressive Forces
Reaction
Action
Compressive Force
Reaction
Action
Tensile Force
• Pushing force on the body -- compressive force
• Pulling force on a body -- a tensile force
Procedure for drawing a free body
diagram
• Step 1: Draw or sketch the body to be
isolated
• Step 2: Indicate all the forces that
act on the particle.
• Step 3: Label the forces with their
proper magnitudes and directions
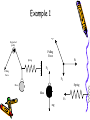
Example 1
Fp
Supported
pulley
Pulling
Force
Fs
Spring
F1
Pulling
Force
F1
Spring
Mass
Mass
Fs
mg
Example 2
Ceiling Support
Ceiling Support
Action Load = 10 N
Ring
Reaction Force = 10 N
Ring
Weight = 10 N
Weight = 10 N
Gravity Load =10 N
Free Body boundary
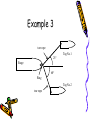
Example 3
tow rope
Tug No.1
25
Barge
60
Ring
.
tow rope
Tug No.2
Solution
• Resultant R of the two forces in two
ropes:
Rx 10 cos 25 30 cos 60 24.06 kN
Ry 10 sin 25 30 sin 60 21.75 kN
Solution
R 24.06 21.75 32.43 kN
2
2
21.75
tan
42.1
24.06
1
Equilibrant E = - R
E = 32.43 kN
42.1
42.1
R = 32.43 kN
Solution
tow rope
Tug No.1
25
Barge
60
Ring
.
Tug No.2
tow rope
Resultant R is the sum of the actions
of the tow ropes on the barge
E=-R
Equilibrant E is the reaction of the barge
to the ropes
Moment and Couple
• Moment of Force
• Moment M of the force F
about the point O is defined
as:
M=Fd
where d is the perpendicular
distance from O to F
• Moment is directional
M
M
oo
dd
FF
Moment and Couple
F
A
r
d
B
M = F.d
= F.r.cos
Moment = Force x Perpendicular Distance
Resultant of a system of forces
l3
O
Rx
F3
l2
l1
l
R
F2
F 3y
F3
R
Ry
F2
F1
F1
F 1x
(a)
F 1y
F 3x
F 2y
F 2x
(b)
An arbitrary body subjected to a number of forces F1, F2 & F3.
Resultant
R = F1 + F2 + F3
Components
Rx = F1x + F2x + F3x
Ry = F1y + F2y + F3y
Resultant Moment
l3
O
Rx
F3
l2
l1
l
R
F2
F 3y
F3
R
Ry
F2
F1
F1
F 1x
(a)
F 1y
(b)
Resultant moment Mo
= Sum of Moments
Mo = F1 l1 + F2 l2 + F3 l3 = R l
F 3x
F 2y
F 2x
Couple
• For a Couple
R =F = 0
But Mo 0
Mo = F(d+l) - Fl = Fd
Moment of couple is
the same about every
point in its plane
O
O
ll
F
F
d
d
F
F
Mo = F d
Example 4
• Calculate the total (resultant)
moment on the body.
300 mm
15 N
30 N
170 mm
30 N
A
100 mm 15 N
50 mm
Example 4 (Solution)
• Taking moments about the corner A
M 30 0.17 15 0.3 30 0.05 15 0.1
30 0.120 15 0.2 6.6 Nm
• Note that the forces form two
couples or pure moments 3.6 Nm and
3.0 Nm (resultant force =0, moment
is the same about any point).
F = 10 N
Exercise
• A
1. What is the moment of the 10 N force
about point A (MA)?
A) 10 N·m
B) 30 N·m
D) (10/3) N·m
E) 7 N·m
C) 13 N·m
d=3m
APPLICATIONS
What is the net effect of the
two forces on the wheel?
APPLICATIONS
What is the effect of the 30 N
force on the lug nut?
MOMENT IN 2-D
The moment of a force about a point provides a measure of the
tendency for rotation (sometimes called a torque).
Moment
F=100
M
L=20
=_____________
Moment
F=32N
L=50cm
L=300mm
+
M=27.5N
F=55N
+
M=-9.6N
EXAMPLE 1
Given: A 400 N force is
applied to the frame
and = 20°.
Find: The moment of the
force at A.
Plan:
1) Resolve the force along x and y axes.
2) Determine MA using scalar analysis.
EXAMPLE 1
Solution
+ Fx = -400 cos 20° N
+ Fy = -400 sin 20° N
+ MA = {(400 cos 20°)(2)
+ (400 sin 20°)(3)} N·m
= 1160 N·m
GROUP PROBLEM SOLVING
Given: A 40 N force is
applied to the wrench.
Find: The moment of the
force at O.
Plan: 1) Resolve the force
along x and y axes.
2) Determine MO using
scalar analysis.
Solution: + Fy = - 40 cos 20° N
+ Fx = - 40 sin 20° N
+ MO = {-(40 cos 20°)(200) + (40 sin 20°)(30)}N·mm
= -7107 N·mm = - 7.11 N·m