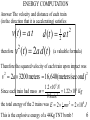* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download bezout identities with inequality constraints
Laplace–Runge–Lenz vector wikipedia , lookup
Photon polarization wikipedia , lookup
Hunting oscillation wikipedia , lookup
Centripetal force wikipedia , lookup
Internal energy wikipedia , lookup
Classical mechanics wikipedia , lookup
Eigenstate thermalization hypothesis wikipedia , lookup
Matter wave wikipedia , lookup
Kinetic energy wikipedia , lookup
Equations of motion wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
Rigid body dynamics wikipedia , lookup
Classical central-force problem wikipedia , lookup
USSC2001 Energy Lecture 2 Kinetic Energy in Motion Wayne M. Lawton Department of Mathematics National University of Singapore 2 Science Drive 2 Singapore 117543 Email [email protected] R:\public_html\courses\Undergraduate\USC\2008\USC2001/ Tel (65) 6516-2749 1 NEWTON’s 2nd LAW The net force on a body is equal to the product of the body’s mass and the acceleration of the body. F ma Question: what constant horizontal force must be applied to make the object below (sliding on a frictionless surface) stop in 2 seconds? v 6m / s 2 FALLING BODIES Consider a particle thrown upward with velocity v0 from the ground at time t = 0 h(t) t h(t 4 ) t2 t1 t4 t t3 Question : What is the particles height h as a function of t and when does the particle hit the ground ? 3 HEIGHT COMPUTATION From Newton’s 2nd Law, the velocity v of the particle as a function of t is given by v(t ) v g t 0 v (t ) v0 therefore h (t ) u t u 0 t1 t v(u ) d u u t u 0 (v0u gu ) | 1 2 2 v0t gt 1 2 and the particle hits the ground at t1 2v0 / g 2 4 ENERGETIC STUPIDITY Fundamentals of Physics by D. Halliday, R. Resnick and J. Walker, p. 117 : "In 1896 in Waco Texas William Crush of the 'Katy' railway parked two locomotives at opposite ends of a 6.4 km long track, fired them up, tied their throttles open, and allowed them to crash head on in front of 30,000 spectators. Hundreds of people were hurt by flying debris; several were killed. Assume that each locomotive weighed 1.2 million Newtons and that its acceleration along the track was equal to a 0.26 meters / second 2 Question : What was the total kinetic energy of the two locomotives just before the collision? 5 ENERGY COMPUTATION Answer The velocity and distance of each train (in the direction that it is accelerating) satisfies v(t ) a t therefore d (t ) a t v (t ) 2a d (t ) 2 1 2 2 (a valuable formula) Therefore the squared velocity of each train upon impact was v 2a 3200 meters 16,640(meters/sec ond ) 2 2 1.2 10 N 5 Since each train had mass m 1 . 22 10 Kg 2 9.8 m/s the total energy of the 2 trains was E 2 12 mv 2 2 108 J 6 This is the explosive energy of a 44Kg TNT bomb ! 6 WORK-KINETIC ENERGY THEOREM Consider a net force that is applied to an object having mass m that is moving along the x-axis The work done is xf W F ( x) dx xi Newton’s 2nd Law F ( x ) ma( x) dv dv dx dv Chain Rule a ( x) v dt dx dt dx Kinetic Energy T ( x ) 1 mv 2 ( x ) 2 xf W m v d v T ( x f ) T ( xi ) xi 7 CONSERVATION OF ENERGY Definition V is a potential energy function if dV ( x) F ( x) dx and in that case we can also compute the work as xf W F ( x) dx V ( xi ) V ( x f ) xi so the total energy E T V is conserved since E ( x f ) T ( x f ) V ( x f ) T ( xi ) V ( xi ) E ( xi ) 8 HARMONIC OSCILLATOR Conservation of energy often provides a method to derive the equations of motion of physical systems. E mx kx 1 2 2 1 2 2 displacement x 0 Energy Conservation E is constant E x x x(t ) a cos ( t ) 0 m x x k x x k m R a 2E k amplitude k angular frequency T 2 period m phase 9 VECTORS AND THEIR GEOMETRY Nonnegative Numbers, Real Numbers, Vectors represent quantities having Magnitude, Magnitude+Sign, Magnitude+Direction u u + multiplication by a scalar v = w geometric vector addition a same vector 1.5u v u -.6u b a b | a | | b | cos scalar product 10 VECTORS AND THEIR ALGEBRA Vectors can be represented by their coordinates u (u1 , u 2 ) u2 u1 and so can vector operations (u1, u 2 ) ( v1, v2 ) (u1 v1, u 2 v 2 ) c (u1, u 2 ) (cv1, cv2 ) (u1, u 2 ) ( v1, v2 ) u1v1 u 2 v2 11 NEWTON’s 3rd LAW & MOMENTUM CONSERVATION When two bodies interact, the forces on the bodies from each other are always equal in magnitude and opposite in direction. F M1 F1 2 M2 The momentum of a body is the product of its mass and velocity, the momentum of a system is the sum of the momenta of its bodies. The momentum of an isolated system is conserved. For two bodies this is derived by applying Newton’s 2nd and 3rd Laws d (M V M V ) F F 1 1 2 2 1 2 dt 0 12 COLLISIONS ALONG A LINE Since when two objects collide the system momentum M1 V1 M2 V2 ' V 1 ' V 2 ' ' is conserved M1V1 M 2 V2 M1V1 M 2 V2 A collision is elastic if the kinetic energy is conserved. 2 2 '2 '2 M1V1 M 2 V2 M1V1 M 2 V2 then M1 M 2 2M2 ' V1 M M V1 M M V2 1 2 1 2 2 M1 M 2 M1 ' V2 M M V1 M M V2 1 2 1 2 13 Inertial Systems and Galilean Transformations Definition 2 physical reference frames are (mutually) inertial if they move with constant relative velocities. This is the case if and only if they admit coordinate systems ( x, y, z , t ) and ( x, y, z , t ) that are related by Definition: Galilean Transformation Equations (GTE) x x vt y y z z t t y y v x vt x x Problem: use GTE to show that the velocities seen in two frames satisfy x V V v 14 TUTORIAL 2 1. (from Halliday, Resnick and Walker, p.162) A 60kg skier starts from rest at a height of 20 m above the end of ski-jump ramp as shown below. As the skier leaves the ramp, his velocity makes an angle of 28 degrees with the horizontal. Ignoring friction and air resistance, use conservation of energy to compute the maximum height h of his jump? 20 m end of ramp 28 h Neglect the effects of air resistance and assume that the ramp is frictionless. 15 TUTORIAL 2 2. Show that for a pendulum with small θ 2 E L m ( g θ Lθ ) 1 2 2 then use conservation of energy to derive the equations of motion for the pendulum. θ L m 3. Derive the two equations on the bottom of page 13. 4. Derive the Principle of Galilean Invariance for elastic collision: kinetic energy is conserved as seen in an inertial reference: Hint: in reference with vel. = v Ebefore 2 2 1 1 M 1 (V1 v) M 2 (V2 v) 2 2 16