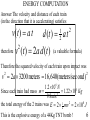Download bezout identities with inequality constraints

USSC2001 Energy
Lecture 2 Kinetic Energy in Motion
Wayne M. Lawton
Department of Mathematics
National University of Singapore
2 Science Drive 2
Singapore 117543
Email [email protected]
R:\public_html\courses\Undergraduate\USC\2008\USC2001/
Tel (65) 6516-2749
1
NEWTON’s 2nd LAW
The net force on a body is equal to the product of
the body’s mass and the acceleration of the body.


F  ma
Question: what constant horizontal force must
be applied to make the object below (sliding on
a frictionless surface) stop in 2 seconds?
v  6m / s
2
FALLING BODIES
Consider a particle thrown upward with velocity v0
from the ground at time t = 0
h(t)
t
h(t 4 )
t2
t1
t4
t
t3
Question : What is the particles height h as a function
of t and when does the particle hit the ground ?
3
HEIGHT COMPUTATION
From Newton’s 2nd Law, the velocity v of the particle
as a function of t is given by v(t )  v  g t
0
v (t )
v0
therefore
h (t )  
u t
u 0

t1

t
v(u ) d u
u t
u 0
 (v0u  gu ) |
1
2
2
 v0t  gt
1
2
and the particle hits the ground at t1  2v0 / g
2
4
ENERGETIC STUPIDITY
Fundamentals of Physics by D. Halliday, R. Resnick and J.
Walker, p. 117 : "In 1896 in Waco Texas William Crush of the
'Katy' railway parked two locomotives at opposite ends of a
6.4 km long track, fired them up, tied their throttles open, and
allowed them to crash head on in front of 30,000 spectators.
Hundreds of people were hurt by flying debris; several were
killed. Assume that each locomotive weighed 1.2 million
Newtons and that its acceleration along the track was equal to
a  0.26 meters / second
2
Question : What was the total kinetic energy of the two
locomotives just before the collision?
5
ENERGY COMPUTATION
Answer The velocity and distance of each train
(in the direction that it is accelerating) satisfies
v(t )  a t
therefore
d (t )  a t
v (t )  2a d (t )
2
1
2
2
(a valuable formula)
Therefore the squared velocity of each train upon impact was
v  2a  3200 meters  16,640(meters/sec ond )
2
2
1.2 10 N
5
Since each train had mass m 

1
.
22

10
Kg
2
9.8 m/s
the total energy of the 2 trains was E  2  12 mv 2  2 108 J
6
This is the explosive energy of a 44Kg TNT bomb !
6
WORK-KINETIC ENERGY THEOREM
Consider a net force that is applied to an object
having mass m that is moving along the x-axis
The work done is
xf
W   F ( x) dx
xi
Newton’s 2nd Law F ( x )
 ma( x)
dv dv dx
dv
Chain Rule a ( x) 

v
dt dx dt
dx
Kinetic Energy T ( x )  1 mv 2 ( x )
2
xf
W   m v d v  T ( x f )  T ( xi )
xi
7
CONSERVATION OF ENERGY
Definition V is a potential energy function if
dV ( x)
F ( x)  
dx
and in that case we can also compute the work as
xf
W   F ( x) dx  V ( xi )  V ( x f )
xi
so the total energy
E  T V
is conserved since
E ( x f )  T ( x f )  V ( x f )  T ( xi )  V ( xi )  E ( xi )
8
HARMONIC OSCILLATOR
Conservation of energy often provides a method to
derive the equations of motion of physical systems.
E  mx  kx
1
2
2
1
2
2
displacement x
 0
Energy Conservation  E is constant  E

x   x
 x(t )  a cos ( t   )
0  m x x  k x x
k
m

R
a  2E k
amplitude
 k
angular frequency T  2 period
m
phase

9
VECTORS AND THEIR GEOMETRY
Nonnegative Numbers, Real Numbers, Vectors
represent quantities having
Magnitude, Magnitude+Sign, Magnitude+Direction
u
u
+
multiplication
by a scalar
v
=
w
geometric vector addition
a
same vector
1.5u
v
u
-.6u

b
a  b  | a | | b | cos 
scalar product
10
VECTORS AND THEIR ALGEBRA
Vectors can be represented by their coordinates
u  (u1 , u 2 )
u2
u1
and so can vector operations
(u1, u 2 )  ( v1, v2 )  (u1  v1, u 2  v 2 )
c (u1, u 2 )  (cv1, cv2 )
(u1, u 2 )  ( v1, v2 )  u1v1  u 2 v2
11
NEWTON’s 3rd LAW & MOMENTUM CONSERVATION
When two bodies interact, the forces on the bodies
from each other are always equal in magnitude
and opposite in direction. F
M1
F1
2
M2
The momentum of a body is the product of its mass
and velocity, the momentum of a system is the sum
of the momenta of its bodies. The momentum of an
isolated system is conserved. For two bodies this is
derived by applying Newton’s 2nd and 3rd Laws
d (M V  M V )  F  F
1 1
2 2
1
2
dt
0
12
COLLISIONS ALONG A LINE
Since when two objects collide the system momentum
M1
V1
M2
V2
'
V
1
'
V
2
'
'
is conserved M1V1  M 2 V2  M1V1  M 2 V2
A collision is elastic if the kinetic energy is conserved.
2
2
'2
'2
M1V1  M 2 V2  M1V1  M 2 V2 then
M1 M 2
2M2
'
V1  M  M V1  M  M V2
1
2
1
2
2 M1
M 2 M1
'
V2  M  M V1  M  M V2
1
2
1
2
13
Inertial Systems and Galilean Transformations
Definition 2 physical reference frames are (mutually)
inertial if they move with constant relative velocities.
This is the case if and only if they admit coordinate
systems ( x, y, z , t ) and ( x, y, z , t ) that are related by
Definition: Galilean Transformation Equations (GTE)
x  x  vt y   y z   z t   t
y
y
v
x
vt
x
x
Problem: use GTE to
show that the velocities
seen in two frames satisfy
x
V V v
14
TUTORIAL 2
1. (from Halliday, Resnick and Walker, p.162)
A 60kg skier starts from rest at a height of 20 m
above the end of ski-jump ramp as shown below. As
the skier leaves the ramp, his velocity makes
an angle of 28 degrees with the horizontal. Ignoring
friction and air resistance, use conservation of energy
to compute the maximum height h of his jump?
20 m
end of ramp

28
h
Neglect the effects of air resistance and assume that
the ramp is frictionless.
15
TUTORIAL 2
2. Show that for a pendulum with small θ
2

E  L m ( g θ  Lθ )
1
2
2
then use conservation of energy to derive
the equations of motion for the pendulum.
θ
L
m
3. Derive the two equations on the bottom of page 13.
4. Derive the Principle of Galilean Invariance for
elastic collision: kinetic energy is conserved as seen in
an inertial reference: Hint: in reference with vel. = v

Ebefore
2
2
1
1
 M 1 (V1  v)  M 2 (V2  v)
2
2
16