Download Potential Energy

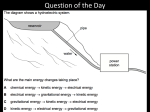
Energy, Work,
and Conservation
Chapters
10 -11
Some Energy Considerations

Energy can be transformed from one form to
another.
◦ The total amount of energy in the Universe never
changes.
◦ This is also true for isolated system.
◦ Energy transformations are essential to the study of
physics, chemistry, biology, geology, astronomy.

Can be used in place of Newton’s laws to solve
certain problems more simply
Mechanical Energy
The focus of this chapter is on mechanical
energy.
 “Mechanical energy is the energy that is
possessed by an object due to its motion
or due to its position.”

Mechanical Energy
Kinetic
Energy
(KE)
Potential
Energy
(PE)
Force, Energy, and Work
Force
Work
Energy
With this relationship we can find
expressions for different forms of PE and
discuss the principle of conservation of
energy and apply it to solving problems.
 The connection between work and energy
can be used in place of Newton’s 2nd law to
solve for certain problems involving force.

What is work?
 “Work”
is the link that ties force and
energy together.
 In physics, work is defined differently than in
everyday life.
 “The work, W, done by a constant force on
an object is defined as the product of the
component of the force along the direction
of displacement and the magnitude of the
displacement.”
Work: General Case
W = (F cos q)x
◦ F is the magnitude of the force
◦ Δ x is the magnitude of the object’s
displacement
◦ q is the angle between F and x
Work: Specific Case
W = F x
◦ This equation applies when the force is in
the same direction as the displacement.
◦ F and x are in the same direction.
Sample Problem
A man cleaning his apartment pulls the
canister of a vacuum cleaner with a force
of magnitude F = 55.0 N. The force makes
an angle of 30.0o with the horizontal. The
canister is displaced 3.00 m to the right.
Calculate the work done by the 55.0 N
force on the vacuum cleaner.
More About Work

This definition of work gives no
information about:
◦ The time it took for the displacement to
occur.
◦ The velocity or acceleration of the object.
◦ These value can be obtained indirectly from
work and then use of PE, KE, and the
conservation of energy.
◦ More on this later.
NO Displacement = NO Work!!


As long as an
object does not
change its
position, no work
is being done.
There are two
other cases when
no work is done.
Can you think of
them?
Force & Displacement Perpendicular
= NO Work!!
If displacement is
horizontal and the applied
force is vertical, the angle
between them will be
90o.
 cos 90° = 0
 Whenever the
displacement and the
applied force are
perpendicular to each
other no work is done.

No Applied Force = NO Work!!
 No
applied
force
means no
work is
done.
 ΣF = 0 N,
W=0J
Multiple Forces and Work
∆x
WT = (ΣFcosθ) ∆x

If there are multiple forces acting on an
object, the total work done is the algebraic
sum of the amount of work done by each
force.
A Quick Summary of Work

Work doesn’t happen by itself.
◦ A net force must be acting on an object and
causing a displacement for work to be done.
Work is done by something in the
environment, on the object of interest.
 The forces discussed here are constant.

◦ The forces could be variable.

Work is related to energy as well.
◦ This will be covered in the next section.
Work and Energy

In the previous section we looked at the
link between work and force.
◦ W = (F cos q)x

In this section we will look at the
relationship between work and energy.
◦ We can use this relationship as an alternative
to solving problems involving Newton’s 2nd
law.
◦ From which we can solve for velocity,
displacement, and acceleration.
Work Causes Displacement
Work does not occur unless displacement
occurs.
 Displacement does not occur unless
speed/velocity is involved.
 Thus, work and speed/velocity are also
related.
 Using work, we can determine the speed
of an object if we know its displacement
and the net forces acting on it.

Determining an object’s speed given
the net force acting on it and the
work done to it.
Kinetic Energy
1
2
KE  mv
2


Energy associated with the motion of an
object.
Scalar quantity with the same dimensions as
work.
◦ SI Units: J

Work is related to kinetic energy.
◦ Wnet = ∆KE = KEf – KEi
Work-Kinetic Energy Theorem
Wnet  KEf  KEi  KE

When work is done by a net force on an object
and the only change in the object is its speed, the
work done is equal to the change in the object’s
kinetic energy.
◦ Speed will increase if work is positive.
◦ Speed will decrease if work is negative.
Work and Kinetic Energy

An object’s kinetic
energy can also be
thought of as the
amount of work a
moving object could
do in coming to
rest.
◦ The moving hammer
has kinetic energy
and can do work on
the nail.
Work and Kinetic Energy

Work can also
be used to
impart KE to an
object.
◦ The golf ball at
rest is given a
velocity and thus
KE because of
the work done
by the club.
Sample Problem
A car of mass 1.40x103 kg being towed
has a net forward force of 4.50x103 N
applied to it. The car starts from rest and
travels down a horizontal highway. Find
the speed of the car after it has traveled
100.0 m. (Ignore kinetic energy losses
caused by friction and air resistance.)
Potential Energy

Potential energy (PE)is associated with
the position of the object within some
system.
◦ Potential energy is a property of the system,
not the object.
◦ A system is a collection of objects interacting
via forces or processes that are internal to
the system.
◦ PE again is only associated with conservative
forces.
Gravitational Potential Energy

Gravitational Potential
Energy is the energy
associated with the
relative position of an
object in space near the
Earth’s surface.
◦ Objects interact with the
earth through the
gravitational force.
◦ The potential energy is for
the earth-object system.
Work and Gravitational Potential
Energy
An expression for PE can be derived using
work.
 The expression for PE shows that it is
determined by the mass of the object, the
gravitational acceleration at the Earth’s
surface, and the vertical location of the
object.

◦ This expression for PE is only valid for object
near the Earth’s surface.
Work and Gravitational Potential
Energy
PE = mgy
 Wgrav ity  PEi  PE f

◦ This equation relates work
to PE.
◦ The work done by PE
depends only on the height
of the object.

A “zero” point must be
established.
◦ More on this in a moment.
Reference Levels for Gravitational
Potential Energy

A location where the gravitational potential
energy is zero must be chosen for each
problem.
◦ The choice is arbitrary since the change in the
potential energy is the important quantity.
◦ Choose a convenient location for the zero
reference height.
 Often the Earth’s surface.
 May be some other point suggested by the problem.
◦ Once the position is chosen, it must remain fixed
for the entire problem.
Example of Reference Levels
At location A, the
desk may be the
convenient reference
level.
 At location B, the
floor could be used.
 At location C, the
ground would be the
most logical reference
level.
 The choice is
arbitrary, though.

Sample Problem
How much work does a bricklayer do to
carry 30.2 kg of bricks from the ground
up to the height of 11.1 m.? What is the
potential energy of the bricks when the
bricklayer reaches this height?
Conservation

Conservation in general:
◦ To say a physical quantity is
conserved is to say that the
numerical value of the quantity
remains constant throughout
any physical process although
the quantities may change
form.
 The form of a physical quantity
may change but the overall
numeric value (or magnitude)
will not.
◦ Conservation plays an
important role in physics and
in other sciences.
Conservation of Mechanical Energy

In conservation of mechanical energy, the total
mechanical energy remains constant.
◦ In any isolated system of objects interacting only through
conservative forces, the total mechanical energy of the
system remains constant.

Total mechanical energy is the sum of the
kinetic and potential energies in the system.
Ei  E f
KEi  PEi  KEf  PEf
◦ Other types of potential energy functions can be
added to modify this equation
Problem Solving with Conservation
of Energy

Define the system
◦ Verify that only conservative forces are present.

Select the location of zero gravitational potential energy,
where y = 0.
◦ Do not change this location while solving the problem.

Identify two points the object of interest moves between.
◦ One point should be where information is given.
◦ The other point should be where you want to find out something.

Apply the conservation of energy equation to the system.
◦ Immediately substitute zero values, then do the algebra before
substituting the other values.

Solve for the unknown:
◦ Typically a speed or a position
◦ Substitute known values
◦ Calculate result
Sample Problem
A sled and its rider together weigh 800 N.
They move down a frictionless hill
through a vertical distance of 10.0 m. Use
conservation of mechanical energy to find
the speed of the sled at the bottom of the
hill, assuming the rider pushes with an
initial speed of 5.00 m/s. Neglect air
resistance.
Potential Energy Stored in a Spring

Spring force is also a conservative force.
◦ Thus a PE expression can be derived for the
spring force and the work a spring does is not
path dependent.
◦ Let’s 1st look at the spring force.


Involves the spring constant, k
Hooke’s Law gives the force
◦ F=-kx
 F is the restoring force
 F is in the opposite direction of x
 k depends on how the spring was formed, the material it
is made from, thickness of the wire, etc.
Potential Energy in a Spring

Elastic Potential Energy
◦ Related to the work required to compress a
spring from its equilibrium position to some
final, arbitrary, position x.
1 2
PEs  kx
2
◦ We can relate this PE to kinetic energy in the
same way we related gravitational PE to
kinetic energy.
Spring Potential Energy
A) The spring is in
equilibrium, neither
stretched or
compressed.
 B) The spring is
compressed, storing
potential energy.
 C) The block is
released and the
potential energy is
transformed to kinetic
energy of the block.

Conservation of Mechanical Energy
Including a Spring

The PE of the spring is added to both sides
of the conservation of mechanical energy
equation to give:
(KE  PEg  PEs )i  (KE  PEg  PEs )f

The same problem-solving strategies apply
to these problems as well.
Sample Problem
A 0.50 kg block rests on a horizontal, frictionless
surface as seen in the figure. The block is pressed
against a light spring having a spring constant of
k=80.0 N/m. The spring is compressed a distance of
2.0 cm and released. Consider the system to be the
spring, block, and Earth and find the speed of the
block when it is at the bottom of the incline.
Energy Transfers

By Work
◦ By applying a force.
◦ Produces a displacement of the system.
◦ Wnc  (KEf  KEi )  (PEf  PEi )

Heat
◦ The process of transferring heat by collisions
between atoms or molecules.
◦ For example, when a spoon rests in a cup of coffee,
the spoon becomes hot because some of the KE of
the molecules in the coffee is transferred to the
molecules of the spoon as internal energy.
More Energy Transfers

Mechanical Waves
◦ A disturbance propagates through a medium.
◦ Examples include sound, water, seismic.

Electrical transmission
◦ Transfer by means of electrical current.
◦ This is how energy enters any electrical device.
More Energy Transfers

Electromagnetic radiation
◦ Any form of electromagnetic waves.
 Light, microwaves, radio waves.
◦ For example
 Cooking something in your microwave oven.
 Light energy traveling from the Sun to the Earth.
Collisions


Momentum is conserved in any collision.
Total KE is not always conserved.
◦ Some KE is converted to other forms of energy (i.e.
internal energy, sound energy, etc.) or is used to do the
work needed to deform an object.

Two broad categories of collisions:
◦ Elastic collisions
◦ Inelastic collisions: Perfectly inelastic and
inelastic
 Elastic
and perfectly inelastic collisions represent ideal
cases of collisions.
 Most real world cases fit somewhere between these
two extremes.
Inelastic Collisions
Momentum is conserved.
 Kinetic energy is not conserved.
 Two categories: inelastic and perfectly
inelastic.

◦ Perfectly inelastic collisions occur when the
objects stick together.
 Not all of the KE is necessarily lost.
 Colliding objects have different initial velocities but
the same final velocities.

Use: m1v1i  m2 v2i  m1v1f  m2 v2f
Perfectly Inelastic Collisions
When two
objects stick
together after the
collision, they
have undergone a
perfectly inelastic
collision.
 Conservation of
momentum
becomes:

m1v1i  m2 v 2i  (m1  m2 )v f
Elastic Collisions

Mostly occurs at the atomic and subatomic
levels.
◦ Macroscopic collisions can only approximate
elastic collisions.

Both momentum and kinetic energy are
conserved for both objects.
◦ No KE is lost as sound, heat, light, etc.

Typically have two unknowns.
◦ Solve the equations simultaneously
m1v1i  m2 v 2i  m1v1f  m2 v 2 f
1
1
1
1
2
2
2
2
m1v1i  m2 v 2i  m1v1f  m2 v 2 f
2
2
2
2
Sample problem
Two billiard balls move
towards one another as
in the figure. The balls
have identical masses,
and assume that the
collision between them
is perfect elastic. If the
initial velocities of the
balls are 30 cm/s and
-20cm/s, what is the
velocity of each ball
after the collision?
Summary of Types of Collisions
In an elastic collision, both momentum and
kinetic energy are conserved.
 In an inelastic collision, momentum is conserved
but kinetic energy is not.
 In a perfectly inelastic collision, momentum is
conserved, kinetic energy is not, and the two
objects stick together after the collision, so
their final velocities are the same.

Final Notes About Conservation of
Energy

We can neither create nor destroy
energy.
◦ The total energy of the universe must always
remain the same.
◦ Another way of saying energy is conserved.
◦ If the total energy of the system does not
remain constant, the energy must have
crossed the boundary by some mechanism.
◦ Applies to areas other than physics.
Power
Often also interested in the rate at which the
energy transfer takes place.
 Power is defined as this rate of energy transfer.

◦

W

 Fv
t
SI units for power are Watts (W).
J kg m2
◦ W  
s
s2
Power

US Customary units are generally hp.
◦ Need a conversion factor
ft lb
1 hp  550
 746 W
s
◦ Can define units of work or energy in terms of units
of power:
 kilowatt hours (kWh) are often used in electric bills.
 This is a unit of energy, not power.
Energy, Work,
and Conservation
THE
END
Chapters
10 -11