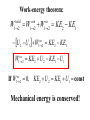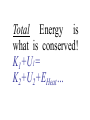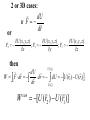Download Lectures 22

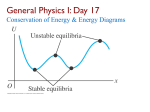
Physics 218: Mechanics
Instructor: Dr. Tatiana Erukhimova
Lectures 22, 23, 24
Work-energy theorem:
total
1 2
W
W
con
1 2
W
nc
1 2
 U 2  U1   W
nc
1 2
nc
1 2
W
nc
1 2
If W
 KE2  KE1
 KE2  KE1
 KE2  U 2  KE1  U1
 0, KE2  U 2  KE1  U1  const
Mechanical energy is conserved!
Examples
Strategy: write down the
total mechanical energy, E,
E = KE + U
at the initial and final
positions of a particle:
Initial E1=KE1+U1…
Final E2=KE2+U2
Then use
nc
1 2
If W
or
 0, KE2  U 2  KE1  U1
H
Water Slide
Who hits the bottom with a faster speed?
The curve of fastest descent
Cycloid – the curve traced by a point on the rim of a circular wheel
as the wheel rolls along a straight line.
Inverted cycloid:
Brachistochrone
http://curvebank.calstatela.edu/brach/brach.htm
Roller Coaster
You are in a roller coaster car of mass M
that starts at the top, height H, with an
initial speed V0=0. Assume no friction.
a) What is the speed at the bottom?
b) How high will it go again?
c) Would it go as high if there were friction?
H
Roller Coaster with Friction
A roller coaster of mass m starts at rest at height
y1 and falls down the path with friction, then
back up until it hits height y2 (y1 > y2).
Assuming we don’t know anything about the
friction or the path, how much work is done by
friction on this path?
Conservative Forces
If there are only conservative forces in the
problem, then there is conservation of
mechanical energy
• Conservative: Can go back and forth along any
path and the potential energy and kinetic energy
keep turning into one another
– Good examples: Gravity and Springs
• Non-Conservative: As you move along a path,
the potential energy or kinetic energy is turned
into heat, light, sound etc… Mechanical energy
is lost.
– Good example: Friction (like on Roller Coasters)
Law of Conservation of Energy
• Mechanical Energy NOT always
conserved
• If you’ve ever watched a roller
coaster, you see that the friction turns
the energy into heating the rails,
sparks, noise, wind etc.
• Energy = Kinetic Energy + Potential
Energy + Heat + Others…
–Total Energy is what is
conserved! K1+U1 = K2+U2+EHeat…
Total Energy is
what is conserved!
K1+U1=
K2+U2+EHeat…



Force of gravity: F  0i  mg j
Potential energy function: U  mgy  Const
Spring:

 
F  kxi  0 j
2
kx
U


Const
Potential energy function:
2
A gun shoots a bullet at angle θ with the x
axis with a velocity of magnitude Vm.
What is magnitude of the velocity when
the bullet returns to the ground? How
high will it go?
Quiz
A block of mass m is placed against a vertical spring,
spring constant k. The spring is unstretched at y=0.
A
If the spring is compressed an amount A and the block
released from rest, how high will it go?
Quiz
A block of mass m is attached to a vertical spring,
spring constant k. The spring is unstretched at y=0.
A
If the spring is compressed an amount A and the block
released from rest, how high will it go?
Block of mass m has a spring connected to
the bottom. You release it from a given
height H and want to know how close the
block will get to the floor. The spring has
spring constant k and natural length L.
H
y=0
ENERGY DIAGRAMS
Potential Energy Diagrams
• For Conservative
forces can draw
energy diagrams
• Equilibrium points
– Motion will move
“around” the
equilibrium
– If placed there with
no energy, will just
stay (no force)
Fx  
dU
dx
0
Stable vs. Unstable Equilibrium
Points
The force is zero at both maxima and minima
but…
– If I put a ball with no velocity there would it stay?
– What if it had a little bit of velocity?
A particle moves along the x-axis while acted on
by a single conservative force parallel to the xaxis. The force corresponds to the potentialenergy function graphed in the Figure. The
particle is released from rest at point A.
a)What is the direction of the force on the particle
when it is at point A?
b) At point B?
c) At what value of x is the kinetic energy of the
particle a maximum?
d) What is the force on the particle when it is at
point C?
e) What is the largest value of x reached by the
particle during its motion?
f) What value or values of x correspond to points
of stable equilibrium?
g) Of unstable equilibrium?
2 or 3D cases:

dU
If F   
dr
or
U ( x, y, z )
U ( x, y, z )
U ( x, y, z )
Fx  
; Fy  
; Fz  
x
y
z
then

U ( r2 )
 


dU 
W   F  dr      dr    dU  U (r2 )  U (r1 )
L

dr
U ( r1 )
W
con


 [U (r2 )  U (r1 )]
Several dimensions: U(x,y,z)
U ( x, y, z )
U ( x, y, z )
U ( x, y, z )
Fx  
; Fy  
; Fz  
x
y
z
Partial derivative is taken assuming all other arguments fixed
Compact notation using vector del, or nabla:

     
F  U ,   i 
j k
x
y
z

dU
Another notation: F   
dr
Geometric meaning of the gradient U
Direction of the steepest ascent;
Magnitude U : the slope in that direction

F  U : Direction of the steepest descent
Magnitude F : the slope in that direction
http://reynolds.asu.edu/topo_gallery/topo_gallery.htm
:
Given the potential energy function
U ( x, y )  
Gm1m2
1
2 2
(x  y )
2
find the x and y components of the corresponding
force.
Have a great day!
Reading: Chapter 9
Hw: Chapter 9 problems and
exercises