Download Work - Regents Physics

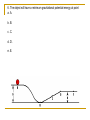
Regents Physics

Work and Energy
Energy and Work


Energy is the ability to Work
Work is the transfer of energy to an object,
or transformation of energy in an object,
when the object moves due to an application
of a force

W = Fd unit is Joules (J)

Energy is also measured in Joules
When is Work Done?



Work is only done when the direction of
motion is in the direction of the force
So we can rewrite the equation to:
W = Fcos  d
F
The F is important!




F = Fg = force due to gravity on an object
In this case, you are doing work against or
with the force of gravity
F = applied force = pushing or pulling
something
F = force of friction  doing work against
friction
The direction is important


The force must be in the direction of motion
For example: A person holds a book and
walks 2 m across the room. Is work being
done against the force of gravity? No!
Force on book
Your motion
Forces are at
90 degrees.
No work is done!
Power  The Rate at Which Work is
Done

Work is done when a force moves an object
in the direction of the force


Work = Force x distance
Power is the rate at which work is done



Power = work (J) / time (s)
Unit of Power is a Watt (W) = J/s
P = Work / time = Fd/t = Fv
Forms of Energy

Energy has many different forms. Here we
discuss the various forms of energy!


Forms of Energy
Stored Energy and Energy of Motion
Forms of Energy

Energy has many forms, including:




Thermal Energy – heat, is the total kinetic energy
possessed by the individual particles of an object
Internal Energy – is the total of the potential and
kinetic energies of an object
Nuclear Energy – is the energy released by nuclear
fission or fusion
Electromagnetic Energy – is the energy associated
with electric or magnetic fields
Stored Energy - Potential Energy



The energy possessed by an object due
to its position or condition
If there is no energy loss due to friction,
the work done to bring an object from its
original position is equal to the object’s
change in potential energy
We can see this in observing changes in
gravitational potential energy
PE = mgh
Gravitational Potential Energy



Objects gravitational potential energy as
they are lifted to a distance above the
Earth’s surface
Work is done against gravity to lift the
object
As long as there is no loss due to friction,
the change in potential energy is due only
to change in height!
PE = mgh
Energy of Motion - Kinetic Energy


Energy associated with
motion
Kinetic energy is gained
as potential energy is
lost
KE = 1/2mv2
M = mass in kilograms
V = velocity in m/s
KE = energy in joules
Conservation of Energy




Just like momentum, energy is also conserved
Energy cannot be created or destroyed, it can only be transferred!
The sum of the changes in a closed system must be equal to zero
We must consider energy conservation under “perfect” and reality
like situations
KE gained = potential energy lost!
Click picture for demo!
Ideal Mechanical Systems


The sum of the kinetic and potential energies in a system is called the
total mechanical energy
Ideal Mechanical System – is a closed system in which no friction or
other nonconservative force acts
 The sum of the kinetic and potential energy changes is equal to zero
 Example: the pendulum
Click above for demo!
Nonideal Mechanical Systems



When a system is acted upon by a nonconservative
force, such as friction, it is called a nonideal mechanical
system
The friction opposes the motion of two objects in contact
with each other and moving relative to each other
The frictional energy is converted into internal energy..an
increase in temperature
Ideal vs. Nonideal
NonIdeal
Ideal
KE = -PE
ET = PE + KE + Q
1/2mv2 = mgh
ET = mgh + 1/2mv2 + Q
Regents Physics

Springs!!
Elastic Potential Energy


Energy is stored in a spring when work is
done stretching or compressing it
This energy is called elastic potential
energy
Compression / Elongation



The compression or elongation of a spring is the change
in spring length from it’s equilibrium position when a
force is applied to it
The compression (elongation) of the spring is directly
proportional to the applied force…provided the elastic
limit of the spring is not exceeded
This gives us an equation!
Hooke’s Law
Fs = kx
The applied force on a spring is proportional
to the distance the spring is displaced (x) and
the spring constant (k)
k is the spring constant and is the constant of
proportionality between the applied force and
the compression/elongation of the spring
Unit is the Newton - meter
Springs Store Energy


Work done to compress/stretch a spring
is equal to the stored potential
energy..just like in gravitation!
Thus…
W = Fsx = ½ kx • x = ½ kx2
PEs = ½ kx2
Click for demo
#1
#2
#3
#4
#5
#6
answers








1) B
2) A takes more work
3) A
4) A
5) A
6) 1000J
7) D
8) B
Use the following diagram to answer questions #5 - #7. Neglect the effect
of friction and air resistance.
5. As the object moves from point A to point D across the frictionless
surface, the sum of its gravitational potential and kinetic energies
a. decreases, only.
b. decreases and then increases.
c. increases and then decreases.
d. remains the same.
6. The object will have a minimum gravitational potential energy at point
a. A.
b. B.
c. C.
d. D.
e. E.
7. The object's kinetic energy at point C is less than its kinetic energy at point
a. A only.
b. A, D, and E.
c. B only.
d. D and E.