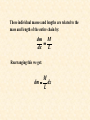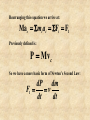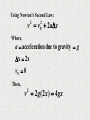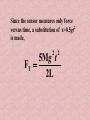* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download The Falling Chain: - College of the Redwoods
Equations of motion wikipedia , lookup
Center of mass wikipedia , lookup
Relativistic mechanics wikipedia , lookup
Fictitious force wikipedia , lookup
Fundamental interaction wikipedia , lookup
Newton's theorem of revolving orbits wikipedia , lookup
Nuclear force wikipedia , lookup
Centrifugal force wikipedia , lookup
Rubber elasticity wikipedia , lookup
Centripetal force wikipedia , lookup
The Force of a Falling Chain By Gina Giacone and Linda Lindsley The Set-up: • “A very flexible uniform chain of length L and mass M is suspended from one end so that it hangs vertically,” the other end is hooked on a force sensor, though it exerts no force at the beginning. The Problem: • To calculate the force that the chain exerts on the sensor as it falls to a position hanging from the hook of the sensor The force exerted by the chain on the sensor is a combination of two forces: •The impulse force(momentum) of each link as it is stopped by the link above it (F1), and •the weight force of the links already hanging from the hook(F2). The total force (FT) exerted on the sensor is: FT = F1 + F2 • The chain itself is made up of links that are individual mass elements (dm), which are associated with their length increments (dx). These individual masses and lengths are related to the mass and length of the entire chain by: dm M dx L Rearranging this we get: M dm dx L Center of Mass: 1 L xc xdm M 0 Velocity of the center of mass: dx c vc dt dx i 1 vc m i M dt m i v i vc M Rearranging the equation: Mvc m i v i p i P The acceleration of the center of mass is: 1 dv c ac M dt dv i 1 a c m i M dt m i a i ac M Rearranging this equation we arrive at: Ma c mi ai Fi F1 Previously defined is: P Mvc So we have a more basic form of Newton’s Second Law: dP dm F1 v dt dt Substituting dm into the previous force equation: M dx F1 v L dt M 2 v L Using Newton’s Second Law: v v 2ax 2 2 0 Where, a acceleration due to gravity g x 2x v0 0 Then, v 2 g( 2 x ) 4 gx 2 Substituting this into the previous equation, M x F1 (4 gx ) 4Mg L L In addition to the force of the falling link, the chain already hanging on the sensor exerts a force equal to its weight force, x F2 Mg L So, the total instantaneous force exerted on the sensor as the final link falls is, FT F1 F2 x x 4M g M g L L x 5M g L Since the sensor measures only force versus time, a substitution of x=0.5gt2 is made, 2 2 5Mg t FT 2L As the final link comes to rest: F Mg Graph of Theoretical Values: 0 -0.05 ____ Falling Force -0.1 ____ Weight Force -0.15 ____ Maximum Force -0.2 -0.25 -0.3 -0.35 -0.4 -0.45 0 0.1 0.2 0.3 0.4 0.5 Experimental Data: Length: 0.7645 m Mass: 0.008479 Kg Weight: 0.0832 N Five times the weight force: 0.4159 N