Download ppt

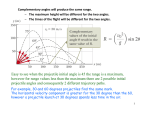
MOTION IN TWO
DIMENSIONS
Some diagrams and simulations from
www.physicsclassroom.com
2 Dimational
Motion
Projectile
Motion
Periodic
Motion
SimpleHarmonic
Motion
Torque
Circular
Motion
Projectile Motion
Newton's laws help to explain the motion (and specifically,
the changes in the state of motion) of objects which are either
at rest or moving in 1-dimension.
One of the most common example of an object which is
moving in two-dimensions is a projectile.
PROJECTILE: is an object upon which the only force
acting is gravity.
EXAMPLES OF PROJECTILES
an object dropped from rest is a projectile
an object which is thrown vertically upwards is also a projectile
an object which is thrown upwards at an angle is also a projectile
MISCONCEPTION:
Some people think that a projectile must have a force acting
upward upon it in order for it to climb. This is not true. A force
is not required to keep an object in motion. A force is only
required to maintain acceleration.
The path of a projectile is not that complicated. Many
projectiles not only undergo a vertical motion, but also
undergo a horizontal motion.
The horizontal and vertical components of the projectile’s
motion are independent of each other.
Vector Combination
Horizontal Motion
Vertical Motion
Forces
Acceleration
No
Yes The force of gravity acts downward
No
Yes "g" is downward at ~ -9.8 m/s/s
Constant
Changing (by ~ 9.8 m/s each second)
Velocity
WHAT IF THE PROJECTILE IS
SHOT UPWARD?
Now assume gravity is turned on
The projectile would
travel with a parabolic
trajectory. The downward
force of gravity will act
upon the cannonball to
cause the same vertical
motion as before - a
downward acceleration.
The cannonball falls the
same amount of distance
in every second as it did
when it was merely
dropped from rest.
Projection Angles
With the same initial speed but different projection angles, a
projectile will reach different altitudes (height above the
ground) and different ranges (distances traveled horizontally).
However, the same range can be obtained from two different
angles, symmetrically around a maximum of 45˚, as shown in
the graph.
Symmetry
The path of a projectile is symmetrical…
It rises to its maximum height in the same time it takes to fall
from that height to the ground.
Because acceleration is the same all of the time, the speed it
loses while going up is the same as the speed it gains while
falling.
Therefore the speeds are the same at equal distances from the
maximum height, where the vertical speed is zero.
Question:
At the instant a horizontally held rifle is fired over level
ground, a bullet held at the side of the rifle is released and
drops to the ground. Ignoring air resistance, which bullet
strikes the ground first?
They strike at the same time.
Question:
A projectile is launched at an angle into the air. If air
resistance is negligible, what is the acceleration of its vertical
component of motion? Of its horizontal component of
motion?
Vertical -9.8 m/s2
Horizontal 0 m/s2
Question:
At what part of its trajectory does a projectile have minimum
speed?
At maximum height.
Question:
A ball tossed into the air undergoes acceleration while it follows a
parabolic path. When the sun is directly overhead, does the
shadow of the ball across the field also accelerate?
NO
Question:
How can an object be moving upward if the only force acting upon it is
gravity?
Newton’s first law
Question:
What launch angle maximizes the range (horizontal distance)?
45°
Question:
What launch angle maximizes the height reached?
90°
Question:
How does the time spent in the air depend on the launch angle?
Time is maximized at 90°
Question:
Compare what happens at complementary launch angles.
Same range (horizontal displacement)
Question:
What happens to the trajectory when the mass of the projectile is
changed?
Nothing
Question:
Compare the trajectories of a projectile that is under the
influence of gravity and one that is not?
NO Gravity (straight line)
Gravity (parabolic trajectory)
Simulation #1
Simulation #2
Do
Q’s 1-4 of Handout
Study Guide 7.1
Q’s 4-8 of Handout
Q’s 1-8 pg 536 & 537 (pdf 67)
Periodic Motion
Periodic Motion
Projectile motion is two-dimensional, but it does not repeat.
Projectiles do not move all along their trajectories more than
once.
Periodic motion can also be an example of 2 dimensional
motion however it involves motion that repeats itself at
regular intervals.
Examples of periodic motion are a yo-yo being swung
horizontally overhead, an object bouncing on a spring or the
pendulum of a clock.
Circular motion
An object that moves in a circle at constant speed is said to
experience UNIFORM CIRCULAR MOTION.
Recall that velocity is a vector quantity so it has both
magnitude and direction.
With circular motion an object may have a constant speed but
a direction that is constantly changing.
If this is the case then the object is said to be undergoing
centripetal acceleration.
Centripetal acceleration: centripetal means center seeking,
or acceleration in the direction of the center of the circle and
can be found using the formula
v v
ac 

t
r
2
Units?
Centripetal acceleration always points towards the center of
the circle and is directly proportional to the square of the
speed and inversely proportional to the radius of the circle.
The velocity of an object undergoing circular motion can
be found using the following formula,
d 2 r
v 
t
T
Where the distance traveled is equal to the circumference of
the circle, and the total time is one period.
PERIOD (T) - the length of time needed to complete one
cycle of motion.
by combining the two above equations we get a second
formula for ac
2
v
ac 
r
 2r 


 T 
ac 
r
2
4 r
ac 
2
T
2
Newton’s second law tells us that an object does not accelerate
unless there is a force that acts on it. For circular motion this
force is called a centripetal force and is also directed radially
inwards.
mv
4 r
f c  mac 
m 2
r
T
2
2
This diagram shows the centripetal force acting in the same
direction as the acceleration. If you remove the centripetal
force, the object will not continue moving in a circular path.
Examples: merry-go-round in the park, tilt-a-whirl, Nascar
banking on the turn at Talledega
Example:
A 0.013 kg rubber stopper is attached to a 0.93 m length of
string. The stopper is swung in a horizontal circle, making
one revolution in 1.18 seconds.
a) Find the speed of the stopper.
b) Find its centripetal acceleration.
c) Find the force that the string exerts on it.
a) 5.0 m/s, b) 26 m/s2, c) 0.34 N
Do
Ring around the collar
Q’s 9-15 Handout
Q’s 15- 19 pg 559 (pdf 68) omit # 17
Simple Harmonic Motion
Simple harmonic motion is another example of periodic
motion.
The key thing with simple harmonic motion is that there
must be a restoring force that causes the object to return
to the equilibrium position.
The restoring force must vary linearly with respect to
displacement.
ie:
small displacement, small force
large displacement, large force
The maximum displacement is called amplitude.
Amplitude: the maximum distance that the object
moves from its equilibrium position.
An example of a type of simple harmonic motion would be
that of a pendulum.
Note that the restoring force here is
the tangential component of the
weight and that it increases with
amplitude.
Similar to the pendulum, the spring is yet another example of
SHM where the restoring force varies linearly with respect to
displacement and is always in the direction of the equilibrium
position.
The period of a simple pendulum and that of a spring can be
found by the following formulas,
Pendulum
Spring
l
T  2
g
m
T  2
k
Example:
On top of a mountain a pendulum 1.55 m long has a period of
2.51 s. What is the acceleration due to gravity at this location?
9.71 m/s2
Example:
A 500 g mass on a spring is displaced by 4.75 cm from its rest
position and is allowed to oscillate. If the period is measured to
be 2.3 sec calculate the spring constant of the spring.
3.7
Example:
Find the length of a pendulum oscillating on the moon that
would have the same period as a 1.0 m long pendulum on earth.
Assuming that the gravity on the moon is 1 sixth that of earth’s.
0.16 m
Example:
A square pig is seen bouncing on a pogo stick with a frequency
on 0.54 Hz. If the pogo stick company advertises that their sticks
have a spring constant of 290, what is the mass of the pig?
25 kg
Do
Q’s 1&2 pg 608 (pdf 75)
Q’s 5-8 pg 614 (pdf 75)
Study Giude7.2
Torque
and
Static Equilibrium
From the chapter on forces we know that if the net force
on an object is zero than the objects net acceleration must
be zero.
if Fnet = 0
than a = 0
Until now we have always assumed that all forces acted on the
center of the object. Now we will look at what would happen if
the forces were located at some distance from the center.
In fact the object would begin to rotate around it’s center of mass.
At first glance this may seem to violate Newton’s laws of motion
because the object begins to rotate even though the net force is zero.
However if you take notice of the center of mass of the object, it
does not move. This is one of the key differences between
translational motion (center of mass moves) and rotational
motion (object rotate around the center of mass)
The force that induces rotational motion is called torque. A
positive torque will cause a counterclockwise rotation and a
negative torque will cause a clockwise rotation.
Torque is measured in Newton meters (Nm), has the symbol
tow (τ) and can be found using the following formula.
  r  f
where r is the distance from the center of mass, or pivot point, to
the position where the tangential component of the force is being
applied.
Example:
Cuddals, a soft and cuddly Rottweiler, wants to go outside.
He pushes on the door with a 45 N force at and angle of 5°
from the perpendicular, 60.0 cm from the hinges. What
perpendicular force is he applying to the door and what is the
final torque?
44.8 N, 26.9 Nm
Example:
Two girls are applying torque to steering wheel (40.0 cm in
diameter) of the bumper car during an amusement park ride.
The girl on the left applies a force of 10.0 N up, while the girl
to write pulls directly down with a force of 15 N. What is the
net torque on the steering wheel?
5 Nm
Conditions for Static Equilibrium
For an object to be truly motionless, it must have a net
force of zero but it also must have a net torque of zero.
Fnet = 0
&
Γnet = 0
Example:
A cable is attached to the
shaft of a 395 kg crane at a
point 5.0 m from the hinged
(pivot) point. When the crane
is horizontal, the cable makes
a 55 degree angle the crane. if
the center of mass is located
halfway between the pivot
point and the cable, and the
Crane is in static equilibrium
what is the tension in the
cable?
2400 N