* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download 198159_WorkEnergy1
Survey
Document related concepts
Transcript
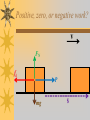
Energy and Work Energy - the ability of a body or system of bodies to perform work. A body is given energy when a force does work on it. But What is Work? A force does work on a body (and changes its energy) when it causes a displacement. If a force causes no displacement, it does no work. Riddle Me This If a man holds a 50 kg box at arms length for 2 hours as he stands still, how much work does he do on the box? ZERO NONE Counterintuitive Results There is no work done by a force if it causes no displacement. Forces perpendicular to displacement, such as the normal force, can do no work. Likewise, centripetal forces never do work. Calculating Work Work is the dot product of force and displacement. Work is a scalar resulting from the interaction of two vectors. Vector Multiplication There are three ways to multiply vectors: •Scalar Multiplication •Dot Product •Cross Product Scalar Multiplication •Magnitude of vector changes. •Direction of vector does not change. F ma If m = 5 kg a = 10 m·s-1 F = 50 N Dot Product Note that the dot W A B product of two vectors gives a scalar . A B AB cos is the angle between A and B. A θ B Dot Product Geometrically, the dot product is the projection of one vector on a second vector multiplied by the magnitude of the second vector. A θ A cos B Calculating Work W F s Fs cos F θ F cos s W F ( x)dx Which does more work? Two forces are acting on the box shown causing it to move across the floor. Which force does more work? F2 θ F1 Vectors and Work F Vectors and Work F s W=F•s W = F s cos 0o W=Fs Maximum positive work Vectors and Work F Vectors and Work F s W=F•s W = F s cos Only the component of force aligned with displacement does work. Work is less. Vectors and Work F Vectors and Work F s W=F•s W = F s cos 180o W=-Fs Maximum negative work. Gravity often does negative work. When the load goes up, gravity does negative work and the crane does positive work. When the load goes down, gravity does positive work and the crane does negative work. F mg Positive, zero, or negative work? A box is being moved with a velocity v by a force P (parallel to v) along a level floor. The normal force is FN, the frictional force is fk, and the weight of the box is mg. Decide which forces do positive, zero, or negative work. Positive, zero, or negative work? v FN fk P mg s Units of Work W F s Fs cos J = N·m J= 2 -2 kg·m ·s Work and variable force The area under the curve of a graph of force vs displacement gives the work done by the force. F(x) xb W = x F(x) dx a xa xb x