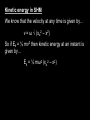Survey
* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download SHM Power points
Document related concepts
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
Relativistic mechanics wikipedia , lookup
Hunting oscillation wikipedia , lookup
Gibbs free energy wikipedia , lookup
Work (thermodynamics) wikipedia , lookup
Kinetic energy wikipedia , lookup
Internal energy wikipedia , lookup
Transcript
Oscillations and Waves Energy Changes During Simple Harmonic Motion Energy in SHM energy velocity Energy-time graphs KE PE Total Note: For a spring-mass system: KE = ½ mv2 KE is zero when v = 0 PE = ½ kx2 PE is zero when x = 0 (i.e. at vmax) Energy–displacement graphs energy KE PE Total -xo displacement +xo Note: For a spring-mass system: KE = ½ mv2 KE is zero when v = 0 (i.e. at xo) PE = ½ kx2 PE is zero when x = 0 Kinetic energy in SHM We know that the velocity at any time is given by… v = ω √ (xo2 – x2) So if Ek = ½ mv2 then kinetic energy at an instant is given by… Ek = ½ mω2 (xo2 – x2) Potential energy in SHM If a = - ω2 x then the average force applied trying to pull the object back to the equilibrium position as it moves away from the equilibrium position is… F = - ½ mω2x Work done by this force must equal the PE it gains (e.g in the springs being stretched). Thus.. Ep = ½ mω2x2 Total Energy in SHM Clearly if we add the formulae for KE and PE in SHM we arrive at a formula for total energy in SHM: ET = ½ mω2xo2 Summary: Ek = ½ mω2 (xo2 – x2) Ep = ½ mω2x2 ET = ½ mω2xo2 Subtitle Text Subtitle Text Subtitle Text Subtitle Text Subtitle Text Subtitle Text Subtitle Text Subtitle Text Subtitle Text Subtitle Text Subtitle Text
