* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Simple Harmonic Motion - The Citadel Physics Department
Survey
Document related concepts
Transcript
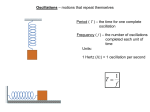
Physics 203 – College Physics I Department of Physics – The Citadel Physics 203 College Physics I Fall 2012 S. A. Yost Chapter 11 Simple Harmonic Motion Physics 203 – College Physics I Department of Physics – The Citadel Announcements Problem set 10B is due Thursday. Read sections 1 – 4 and 7 – 9 if you haven’t Topics: simple harmonic motion, intro to waves. Next Tuesday: Ch. 11, sec. 7 – 9 and 11 – 13 with some material from Ch. 12, sec. 1 – 4 & 7 mixed in. (The topics are related.) Physics 203 – College Physics I Clicker Question Are you here? A = Yes B = No C = Both D = Neither E = Can’t be determined Department of Physics – The Citadel Physics 203 – College Physics I Department of Physics – The Citadel Hooke’s Law From chapter 6: Hooke’s Law describes a linear restoring force when a spring is displaced from its equilibrium position. x F = -k x Elastic potential energy: U = ½ kx2 Physics 203 – College Physics I Department of Physics – The Citadel Simple Harmonic Motion When a mass oscillates under a linear restoring force F = -kx, the acceleration is always opposite the displacement from equilibrium, but proportional to it. a = F/m = -(k/m) x. This is called simple harmonic motion. Physics 203 – College Physics I Department of Physics – The Citadel Circular Motion Analogy y v Where else have we seen a linear restoring force? Look at uniform circular motion in components. m r x Physics 203 – College Physics I Department of Physics – The Citadel Circular Motion Analogy The acceleration vector always points toward the center and has magnitude → y v → a= a v2/r → r v=rw x a= w2 r In vectors: → m → a = - w2 r Physics 203 – College Physics I Department of Physics – The Citadel Circular Motion Analogy The components of the acceleration vector → a= - → 2 w r y → a are m → ax = - w2 x ay = - w2 y The acceleration in each direction is proportional to the displacement. r x Physics 203 – College Physics I Department of Physics – The Citadel Circular Motion Analogy Just focus on the x component: a = - w2 x This is simple harmonic motion, if we match the Hooke’s Law condition: a = F/m =- (k/m) x. Identify the angular velocity for SHM as ___ w = √k/m y → a m → r x Physics 203 – College Physics I Department of Physics – The Citadel Circular Motion Analogy Circular motion x = r cos q = r cos wt The maximum value of x is called the amplitude. In SHM, it is usually written as A: x = A cos wt y → a m q → r x Physics 203 – College Physics I Department of Physics – The Citadel Simple Harmonic Motion General feature of simple harmonic motion: The frequency doesn’t depend on the amplitude. No matter how far you displace the object from equilibrium, w = √ k/m Physics 203 – College Physics I Department of Physics – The Citadel Simple Harmonic Motion x = A cos wt with angular frequency w = √ k/m T = 2p/w is the period of the motion. A x 0 t T -A f = 1/T = w/2p is the frequency of the motion. Units: 1/s = Hz. Physics 203 – College Physics I Department of Physics – The Citadel Circular Motion Analogy The velocity vector in uniform circular motion has magnitude v = rw and is perpendicular to the radius vector: vx = - r w sin q vy = -r w cos q, q = wt For SHM, take the x component, with r →A: v = - A w sin wt → y v q m → q r x Physics 203 – College Physics I Department of Physics – The Citadel Simple Harmonic Motion v = - A w sin wt x= A cos wt Note that v = 0 at the turning points x = ± A. The maximum speed is vmax = Aw, where x = 0. A x v=0 0 t vmax -A Physics 203 – College Physics I Department of Physics – The Citadel Simple Harmonic Motion Acceleration: a = F/m = - k x/m = - w 2 A cos wt Note that a = 0 at the equilibrium points x = 0. The maximum acceleration is amax = w2A a = - w2A A x 0 t a=0 -A a = +w2A Physics 203 – College Physics I Department of Physics – The Citadel Simple Harmonic Motion Energy is conserved: K = ½ mv2, Total energy: U = ½ kx2. E = K + U = ½ kA2. •The potential energy is maximum at the turning points. •The kinetic energy is maximum at the equilibrium position. Kmax = ½ mvmax2 = ½ kA2 → vmax = Aw. Physics 203 – College Physics I Department of Physics – The Citadel Example A 3.0 kg object is attached to a spring with k = 280 N/m and is oscillating in SHM. When it is 2.0 cm from equilibrium, it moves 0.55 m/s. What is the frequency of the motion? ___ ______________ w = √k/m = √(280 N/m) / 3.0 m = 9.66 s-1 f = w/2p = 1.5 Hz Physics 203 – College Physics I Department of Physics – The Citadel Example A 3.0 kg object is attached to a spring with k = 280 N/m and is oscillating in SHM. When it is 2.0 cm from equilibrium, it moves 0.55 m/s. What is the amplitude of the motion? K = ½ mv2, Total energy: U = ½ kx2. E = K + U = ½ kA2 = ½ mv2 + ½ kx2 A2 = (m/k) v2 + x2 = (v/w)2 + x2 = [(0.55 m/s)/(9.66 s-1)]2 + (0.020 m)2 = 0.00364 m2 A = 0.060 m = 6.0 cm. Physics 203 – College Physics I Department of Physics – The Citadel Example A 3.0 kg object is attached to a spring with k = 280 N/m and is oscillating in SHM. When it is 2.0 cm from equilibrium, it moves 0.55 m/s. What is the maximum force on the object? F = kA = (280 N/m) (0.060 m) = 17 N. What is its maximum speed? vmax = Aw = (0.060 m) (9.66 s-1) = 0.58 m/s