* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Making rating curves - the Bayesian approach
Survey
Document related concepts
Transcript
Making rating curves - the
Bayesian approach
Rating curves – what is wanted?
A best estimate of the relationship between
stage and discharge at a given place in a river.
The relationship should be on the form
Q=C(h-h0)b or a segmented version of that.
Q=discharge, h=stage.
It should be possible to deal with the
uncertainty in such estimates.
There should also be other statistical
measures of the quality of such a curve.
These measures should be easy to interpret
by non-statisticians.
Making rating curves the old
fashioned way
For a known zero-stage, the rating curve
can be written as q=a+bx, where
q=log(Q), x=log(h-h0) and a=log(C).
For a set of measurements, one can
then do linear regression with q as
response, x as covariate and a and b as
unknown linear parameters. Minimize SS
analytically (standard linear regression).
The old approach – handling c=-h0
The problem is that the effective bottom level,
h0=-c, is not known.
Solution: Minimize SS by stepping through all
possible values of c.
The advantage: This is the same as
maximizing the likelihood for the regression
problem: qi=a+b log(hi+c)+εi or Qi=C (hi-h0)b Ei
where εi ~ N(0,σ2) is iid noise and Ei= eε .
This model makes hydraulic and statistical
sense!
i
Problems with the old approach
We have prior information about curves
that we would like to use in the
estimation.
Inference and statistical quality
measures are difficult to interpret.
Difficult to get a grip on the discharge
estimate uncertainty.
There is a chance that one gets infinite
parameter estimates using this method!
Bayesian statistics
Frequentistic: treats the parameters as fixed
and finds estimators that will catch their values
approximately.
Bayesian: treats the parameters as having a
stochastic distribution which is derived from
the observations and to prior knowledge.
Bayes’ theorem: f( θ | D) = f( D | θ)f(θ)/f(D)
where f stands for a distribution, D is the data
set and θ is the parameter set.
Prior knowledge
Prior info about a and b can be obtained from
already generated rating curves (using the
frequentistic approach) or by hydraulic
principles.
Prior info about the noise can be obtained
from knowledge about the measurements.
Problem: Difficult to set the prior for the
location parameter h0=-c, but we know it will
not be far below the stage measurements.
Prior knowledge of a and b from the database
Histogram of generated a’s
from the database. Normal
approximation seems ok.
Histogram of generated b’s
from the database. Normal
approximation seems less fine, but
is used for practical reasons.
Bayesian regression
Data given parameters is the same here;
qi=a+b log(hi+c)+εi . D={hi, qi}i=1…n
Problem; even though we have prior info, this
does not give us the form of the prior f(θ),
θ=(a,b,c,σ2).
If the priors are on a certain form, one can do
Bayesian linear regression analytically;
qi=a+b xi+εi for xi=log(hi+c) for a given c.
Same thought as for the frequentistic
approach, handle a,b and σ2 using a linear
model, and handle c using discretization.
Problems with Bayesian regression
While this gives us the form of f(a,b,σ2), it does
not give us the form of f(c).
We know that the stage levels are not too far
above the zero-level. We’d like to code this
prior info but we don’t want to use the stage
measurement (using them both in the prior
and the likelihood).
Jeffrey’s priors containing the covariates is a
general problem with the Bayesian regression
approach! Ok, if you really are in a regression
setting, but this is not the case here.
Problems with the first Bayesian
approach
The form that makes the linear
regression analytical is rather strange.
It requires the form of the prior for σ2
which influences the priors for (a,b).
However, prior info about these two
would be better kept separate.
Difficult to set the prior info for users.
Expected discharge is infinite in this
approach! (Median will be finite.)
A new Bayesian regression
approach
Using a semi conjugate prior, (a,b)~N2,
independent of σ2~IG, we separate
knowledge about a,b and σ2.
We can no longer handle (a,b,σ2) analytically
for known c.
However, (a,b,c,σ2) can be sampled using
MCMC methods.
The sampling method must be effective, since
users do not want to wait to long for the
results.
A graphical overview of the new model
Hyper-parameters:
Parameters:
Measurements:
µa Va ρ µa Vb
σ2
a b
hi
α β
qi
For i in {1,…,number
of measurements}
Sampling methods and efficiency
Naïve MCMC: The Metropolis algorithm. Problem:
(a,b,c) are extremely mutually dependent.
Metropolis or independence-sampler for c, Gibbs
sampling for (a,b, σ2). Dependency of (a,b,c) makes
trouble here, too.
Solution: Sample (a,b,c,σ2) together and then do a
Metropolis-Hastings accepting. Sample c using first
adaptive Metropolis, then indep. sampler. Sample
(a,b,σ2 ) given c and previous σ2 using Gibbs-like
sampling. Then accept/reject all four.
σi-12
Iteration: i-1
ci
i
ai,bi
σi2
Estimation based on simulations
We can estimate parameters using the
sampled parameters by either taking the mean
or the median.
We can estimate the discharge for a given
stage value, either by mean or median
discharge from the sampled parameters or by
discharge from the mean or median
parameters.
Simulations show that median is better than
mean.
Inference based on simulations
Uncertainty in the parameters can be
established by looking at the variance of
sampled parameters.
Credibility intervals can be arrived at
from the quantiles of the parameters.
Discharge uncertainty and credibility
intervals can be obtained by a similar
approach to the discharge for the drawn
parameters.
Example – rating curve with uncertainty:
Rating curve - Q(h) = C (h-h0)^b
m^3/s
Best estimate not conditioned on the parameters - median
Best estimates conditioned on median parameters, h0= -3.076, C=e^a= 11.717, b= 2.486
Upper limit for 95% credibility interval
Lower limit for 95% credibility interval
Frequentist prediction, h0=-99.650000, C=e^a=0.000000, b=65.187747
Measurements
800
700
600
500
400
300
200
100
0
-2
-1
0
1
2
m
Example – prior to posterior
Prior of b.
Posterior of b.
Example - diagnostic plots
Scatter plot of simultaneous
samples from a and b. Note
the extreme correlation
between the parameters.
Residuals. Note the “trumpet” form.
There is heteroscedasticy here, which
the model does not catch.
What has been achieved
Discharge estimates with lower RMSE
than frequentistic estimates.
Measures of estimation uncertainty that
are easy to interpret.
Hopefully, quality measures should be
less difficult to understand.
The distribution of parameters can be
used for decision problems. (Should we
do more measurements?)
What remains
Multiple segmentation.
Need to find good quality measures in addition to
estimation uncertainty. Possibility: Calculate the
probability of more advanced models.
Learning about the priors: A hierarchical approach.
There is still some prior knowledge that has not found
it’s way into the model; namely distance between zerostage and stage measurements.
Heteroscedasticy ought to be removed.
Should have a prior on b that closer reflects both prior
knowledge (positive b) and the database collection of
estimates. For example: b~logN. But this introduces
problems with efficiency.
A graphical view of the model and a
tool for a hierarchical approach
distribution with or without hyper-parameters
hyper- parameters:
parameters:
measurements:
µa Va ρ µb Vb
aj bj
hj,i qj,i
σj2
α β
For j in {1,…,number of stations}
For i in {1,…,number of
measurements for station j}
Solution to the prior for h+c
Possible to go from a regression situation to a model that
has both stochastic discharge and stage values.
~
Possibility: A structural model where real discharge, qi,
~
has a distribution. The real stage,hi , is a deterministic
function of the curve parameters, (a, b, c). Observations,
D=(qi, hi), are the real values plus noise.
The model gives a more realistic description of what
happens in the real world. It also codes the prior
knowledge about the difference between stage
measurements and zero-stage, through the distribution of
q and the distribution of (a, b).
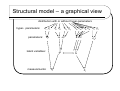
Structural model – a graphical view
distribution with or without hyper-parameters
hyper- parameters:
αε βε
parameters:
µ0 σ0
µq σq2
σε2
q~i
latent variables:
measurements:
αq βq
qi
µb Va ρ µb Vb αδ βδ
σh2
abc
~
hi
hi
Advantage and problems of a
structural model
Advantage:
More realistic modelling of
the measurements and the
underlying structure.
Codes prior knowledge about
the relationship between
stage measurements and the
zero-stage.
Can solve heteroscedasticy.
Gives a more detailed picture
of how measurement errors
occur.
Since b can not be sampled
using Gibbs, we might as well
use a form that insures
positive exponent.
Problem:
Difficult to make an efficient
algorithm.
More complex. Thus even if it
codes more prior knowledge,
the estimates might be more
uncertain. This has not been
tested.