Download Introduction to Statistics - Department of Statistics and Applied

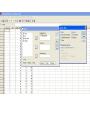
Confidence intervals
Estimation and uncertainty
Theoretical distributions require input parameters.
For example, the weight of male students in NUS follows a Normal(, 2)
distribution. How do we know what should  and 2 be?
We can model the hourly number of admissions to the A&E department at
NUH using a Poisson(2.8) distribution. How is the figure of 2.8 obtained?
In comparing between the heights of male and female students in NUS, one
strategy is to compare the mean heights between the two groups of
students. What does this mean and how do we quantify that there is a
genuine biological difference versus an artefactual difference?
Data exploration and Statistical analysis
1. Data checking, identifying problems and characteristics
2. Understanding chance and uncertainty
3. How will the data for one attribute behave, in a
theoretical framework?
4. Theoretical framework assumes complete information,
need to address uncertainties in real data
Data
Data exploration,
categorical / numerical
outcomes
Model each outcome with
a theoretical distribution
Estimation of parameters,
quantifying uncertainty
Estimation
Generally, before any statistical comparisons can be made, there are always
parameters that need to be estimated.
Recall the bridge between the sample and the population.
In most situations in applied
research, especially in biomedical
sciences, the key interest is what
happens in the population. The
sample is really a way of estimating
what will happen in the population.
Example 1:
Let’s supposed the Science Faculty is interested to compare between the
weights of male and female students in NUS. How will this study be
designed?
- Key interest is to summarise the weight of all the male students in NUS,
and the weight of all the female students in NUS.
- Reasonable assumption that the weight of the students for each respective
gender will be normally distributed.
- Randomly sample 200 male students and 200 female students and
measure their weight.
- Calculate the mean weight of these 200 male students, and use this
quantity to estimate the mean weight of all the male students in NUS.
- Similarly calculate the mean weight of these 200 female students and use
this to estimate the mean weight of all the female students in NUS.
- While we can compare the estimated mean weights of the male and female
students, but how do we know any difference is not due to sampling bias?
- Can we quantify the uncertainty in the estimation, when we use the
calculated sample mean weight to estimate the population mean weight?
Confidence intervals
• Not sufficient to just provide an estimated quantity, need
to quantify the extent of uncertainty involved in the
estimation.
Mean age (54.6 years)
20
30
40
50
60
70
80
AGE
• Assumes data has a bell-shaped / symmetric distribution,
confidence intervals calculated about the mean.
Remarks on Confidence Intervals
• Interval is random, parameter to be estimated is not.
• Width of interval is a measure of precision. Confidence
level as a measure of accuracy.
• Width of CI depends on the magnitude of the uncertainty
(standard error), and level of confidence required.
• Assumptions must be satisfied before constructing CIs.
Mean age (55.2
(54.6 years)
20
30
40
50
60
AGE
70
80
Calculating confidence intervals
• Confidence intervals can be calculated for any estimated
quantities
• Fundamentally related to the concept of quantifying the
degree of uncertainty in the estimation
• Calculate the quantity of interest (sample mean, sample
proportion, etc. – to be covered over the remaining
sessions)
• Calculate the standard error associated with estimating
the quantity.
Quantity of interest
Standard deviation and standard error
• Two extremely different concepts!
Standard deviation (SD)
Used to quantify the variability or dispersion (spread) in a collection of
numbers. It quantifies the ‘distance’ from the average/mean of the data. This
is used to summarize the distribution of a collection of numbers.
A large SD means the collection of numbers is widely dispersed about the
mean, while a small SD means the numbers are concentrated about the
mean value.
Standard error (SE)
Used to quantify the degree of uncertainty in estimating the population mean
with the sample mean.
A large SE indicates that there is considerably uncertainty that the sample
mean is a good estimate for the population mean.
95% Confidence Intervals
• 95% confidence intervals linked to 2 standard errors away
from the mean (or 1.96 SE away from the mean)
• Most common form of CI produced in research.
• Will explore more about CI in subsequent lectures
90% CI
99% CI
Sample mean
Standard deviation
Interpreting Confidence Intervals
• If we were to:
• repeat the experiment 100 times
• construct 95% CI for each time
• Then we would expect 95 of the CIs to cover or include
the true population value.
Confidence intervals and RExcel / SPSS
Consider the mathematics and omega3 consumption dataset that can be
downloaded from
http://www.statistics.nus.edu.sg/~statyy/ST1232/bin/mathematics.xls
Calculate the confidence interval for the mean of the marks before the start
of omega3 consumption.
= (67.95, 70.08)
What about the confidence interval for the mean omega 3 consumption?
Students should be able to
• understand the concept of estimation and how it leads to
uncertainty in statistics
• differentiate between a standard deviation and a standard
error
• understand how a confidence interval is constructed
• understand and interpret a confidence interval
• calculate the confidence interval in RExcel and SPSS when
given the data
• know the assumption required for the use of a confidence
interval