Download Ch13 - People @ TAMU Physics

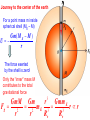
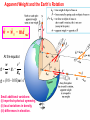
Gravitation
Newton’s law of universal gravitation (1687):
Gm1m 2
F
r2
G  6 . 67  10  1 1 N m 2 / kg 2
Magnitude F~1μN
for m1=m2=
= 100 kg
at r = 1 m
is very
small.
r
Sir Henry Cavendish (1731-1810)
(a torsion balance)
Concept of fields
for forces that
act at a distance
Principle of superposition of forces from different sources:
Weight w  F grav


F   Fj
Gm E m

depends on r.
2
r
On earth’s surface w = mg
Cavendish’s mass of the earth
gR E2
mE 
 6  10 24 kg
G
j
GmE
g 2
RE
(since RE = 6380 km)
Gravitational Potential Energy: Wgrav= U1 - U2
r2
r2
dr GMm GMm
 GMm 
W grav     2 dr  GMm  2 

r 
r
r2
r1
r1 
r1
Let us choose U to be zero at infinity r = ∞:
Gravitational force is conservative !
dU
d  GMm 
GMm
Fr  
  
 2
dr
dr 
r 
r
GMm
U 
r
Derivation of the gravitational potential energy
U = mgy near the earth’s surface ( r = RE+y )
GM E m  GM E m 
 
U E  U (r )  U ( RE )  
  
RE  y 
RE 
y
GM E
 GM E m
m
ymgy
2
RE ( RE  y )
RE
Journey to the center of the earth
For a point mass m inside
spherical shell (ME – M)
Gm(M E  M )
U 
r
The force exerted
by the shell is zero!
Only the “inner” mass M
contributes to the total
gravitational force
3
GmM Gm
r
Gmm E
Fg 
 2 mE 3 
rr
2
3
r
r
Re
Re
Exam Example 27: Motion in the gravitational field of two bodies
(problem 13.58)
M
1

F1
0
m
X
0
X
1
M
ΔX=X-X
0

F2
X
2
X
2
Data: masses M , M , m; positions x , x , x , x; v(t=0)=0
1 2
1 2 0
Find: (a) change of the gravitational potential of the test particle m;
(b) the final speed of the test particle at the final position x;
(c) the acceleration of the test particle at the final position x.
 1
1
 x x  xx
1
 0 1
Solution: (a) U  U  U 0  GM 1m

 1
1
  GM 2 m

 x x  xx
2

 0 2




1 2
(b) Energy conservation: K  U  mv  U  v   2U / m
2
 M2
nd
M1 


(c) Newton’s 2 law: a x  F2 x  F1x  / m  G
2
2 
  x2  x   x1  x  
The Motion of Satellites
Orbits are closed or open.
Open orbits
V2(r→∞) Open orbits are parabolic or hyperbolic.
Closed orbits are elliptical or circular.
There is only one speed that a satellite
can have in a given circular orbit r :
Closed
orbits
V1(r=RE)

v
GM E m mv 2
F g  ma c 

v
2
r
r 3/ 2
2r
2 r

Period: T 
v
GM E
GM E
r
“Synchronous satellites” for digital satellite system TV:
T=1 sidereal day= 24 h(365-1)/365= 23 h 56 m, r =40000 km
Global Positioning System (GPS) : 24 satellites
Space speeds: 1st- to stay in orbit r = RE V1=(GME/RE)1/2=(gRE)1/2=8 km/s
V3
nd- to leave the earth K = - U, mV 2/2 = GM m/R ,
2
2
E
E
Earth V =29.8km/s
e-s
Re=150 Mkm
Sun
V2 =(2GME/RE)1/2 =(2)1/2 V1 =11.2 km/s (parabolic or escape speed)
3rd- to leave the sun V3= 16.7 km/s > V2(sun) – Vearth-sun=
=[(2)1/2-1](GMsun/Rearth’s-orbit)1/2 = 0.41 (29.8 km/s)= 12.3 km/s
since both the sun’s and earth’s grav. attractions act.
Remark: Conservation of energy yields another relation between r and v,
m v 2 / 2  G M m / r  co n st , that does not contradict to r×v=const along a trajectory.
Pioneer-10: Earth (1972)→ Jupiter→ Pluto (1983)→ Solar system’s border (2002)→ star in Mly
On December 18, 2004, Voyager 1 passed the termination shock. This marks the point where the solar wind slows
to subsonic speeds. This is the unofficial date of departure from the Solar System. While the spacecraft still remains
under the sun's influence, at the termination shock particles from the interstellar medium interact with solar
particles, signaling that the hypothetical heliopause is not far from this point. Six years later in 2010 Voyager 1
entered an area of the heliosheath where the solar wind outward speed is 0, or flowing sideways relative to the sun.
This signaled that Voyager 1 was getting very close to entering the interstellar medium.
On December 5, 2011, it was announced that Voyager 1 had entered a new region referred to as a "cosmic
purgatory" by NASA. Within this stagnation region, charged particles streaming from the sun slow and turn inward,
and the solar system's magnetic field has doubled in strength as interstellar space appears to be applying
pressure. Energetic particles originating in the solar system have declined by nearly half, while the detection of
high-energy electrons from outside has increased by 100 fold. The inner edge of the stagnation region is located
approximately 113 astronomical units (AU) from the sun, while the outer edge is unknown.
At a distance of 150 AU as of November 2014, it is the farthest man-made object from Earth and the first probe that
left the Solar System. Voyager 1 had crossed the heliopause (which is the outermost layer of heliosphere) at 121 AU
and entered interstellar space on August 25, 2012. In 300 years it will reach the Oort cloud of long-period comets,
regarded as the outermost zone of the Solar System. It is expected to continue its mission until 2025. "Pale Blue Dot:
A Vision of the Human Future in Space" by Carl Sagan, http://www.youtube.com/watch?v=StN5D3JKB7Y&t=300

v

Exam Example 28: Satellite in a Circular Orbit
Data: r = 2RE , RE = 6380 km
Find: (a) derive formula for speed v and find its value;
(b) derive formula for the period T and find its value;
(c) satellite’s acceleration.
r
Solution: use the value g = GME/RE2 = 9.8 m/s2
(a) The only centripetal force is the gravitational force:
ac
GM E m mv 2
Newton' s 2 nd law  Fg  ma c 

v
2
r
r

GM E RE2

2
RE r
RE2
g

r
m


F grav  F c
ME
RE=6380 km
GM E

r
gRE
 9.8 m / s 2  3.19 10 6 m  5.6 km / s
2
(b) The period T is a time required for one orbital revolution, that is
 r 
2 r
2 r
2 r
2 r
T



 2  
v
RE 
GM E
GM E
GM E

RE
r
RE2
3/ 2
3/ 2
3/ 2
6
RE
6
.
38

10
m
 2 23 / 2
 4h
2
g
9.8 m / s
(c) Newton’s second law with the central gravitational force yields
atan = 0 and arad = ac = Fg/m = GME/r2 = (GME/RE2) (RE/r)2 = g/4 = 2.45 m/s2
Kepler’s Laws of Planetary Motion (1609, 1619)
Heliocentric world system (Copernicus, 1543) vs. Geocentric world system (Ptolemei)
1600-Giordano Bruno burned at the stake by Church for heresy: Copernican system, sun=star, eternal plurality of worlds
1. Each planet moves in an elliptical orbit, with the sun at one focus of the ellipse
Eccentricity e = (Center O to Focus S) / (Semi-major axis a)
The earth’s orbit has e = 0.017. Pluto (e =0.248) is not 9th planet, it is a dwarf planet!
2. A line from the sun to a given planet sweeps out equal areas in equal times.


Proof is based on the angular momentum conservation
from the fact
that follows
that the gravitational force is a central force dL / dt    r  Fgrav  0 


L | r  mv | const  rv sin   2dA / dt  const
3. The periods of the planets are proportional to the
3/2 powers of the major axis lengths of their orbits:
2 a 3 / 2
T
GM sun
Note: Kepler (1571-1630) discovered laws of
planetary motion ~100 years before Newton
(1642-1727) formulated laws of mechanics (1687) !
1633- Galileo Galilei sentenced by Church to imprisonment
Recent discovery: planets in orbit around thousands of other
stars via detection of the apparent “wobble” of a star near the center of mass.
Exam Example 29: Satellite in an Elliptical Orbit (problem 13.67)
Data: hp , ha , RE= 6380 km, ME= 6·1024 kg
Find: (a) eccentricity of the orbit e; (b) period T; (c) arad;
(d) ratio of speed at perigee to speed at apogee vp/va;
(e) speed at perigee vp and speed at apogee va;
hp 2RE
(f) escape speeds at perigee v2p and at apogee v2a.
Solution: (a) rp =hp+RE, ra= ha+RE, a =(rp+ra)/2,
ea = a – rp, e = 1 – rp/a = 1- 2rp/(rp+ra) =
= (ra- rp)/(ra+ rp) = (ha-hp)/(ha+hp+2RE)
 (apogee)
a rad 
(perigee)

v p
v2 p

Fgrav
va
ha
(b) Period of the elliptical orbit is the same as the period of the
circular orbit with a radius equal to a semi-major axis R = a, i.e., T
(c) Newton’s 2nd law and law of gravitation: arad= Fgrav/ m = GME/r2.
2a 3 / 2

GM E
(d) Conservation of angular momentum (La= Lp) or Kepler’s second law:
rava= rpvp, vp/va= ra/rp
(e) Conservation of mechanical energy K + U = const :
mv 2p GM E m mv a2 GM E m mv 2p r p2 GM E m
2GM E ra v  v r p  2GM E r p





 vp 
; a
p
2
ra
ra ( r p  ra )
2
rp
2
ra
2 ra
ra
r p ( r p  ra )
(f) Conservation of mechanical energy for an escape from a distance r
(the second space speed) :
mv 22 G M E m

 v2 
2
r
2G M E
 v2 p 
r
2G M E
,
rp
v 2a 
2G M E
ra
Apparent Weight and the Earth’s Rotation
 

w  w 0  m a rad
At the equator:
w
v2
g   g0 
m
RE
g  (9.8  0.03)m / s 2
Small additional variations:
(i) imperfect spherical symmetry,
(ii) local variations in density,
(iii) differences in elevation.
Circular motion can occur only at r > 1.5 RS.
Black Holes
Event horizon at Schwarzschild radius
At r = 1.5 R its velocity is v = c.
2GM
2GM
RS  2  Vescape 
c
c
RS
RSsun= 3 km, RSearth= 1 cm
GMm
Black-hole potential well U  
r
Energy
E0=K0+U0>0 (free escape)
r
0
E0=K0+U0<0 (trapped state)
E=E0+Wnc (dissipative fall into black hole)
2
mv
GMm

 E 0  W nc
2
r
2 a 3 / 2
4 2 a 3
T
M
GT 2
GM
Objects fall into the black hole in a finite proper time Δt ~ RS/c,
but infinitely long for a distant observer, and are affected by
gravitational red shift, time dilation, and tidal forces effects !
All information is lost inside black hole for outside observers.
“Black holes have no hair” and can be entirely characterized by
energy, momentum, angular momentum, charge, and location.
Supermassive black hole at the center of our Milky Way galaxy
Sagittarius A*: RS = 8·106 km, M = 4·106 Msun = 8·1036 kg
Cone of gravitational capture
( for v2/2 = GM/r )
4RS
Black hole is a bright source
due to an accretion disk !
2RS
Primordial Black Holes and γ-Ray Bursts
1.5RS
RS
M
2a