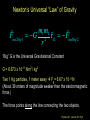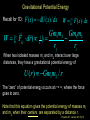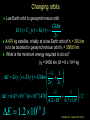Download Physics 207: Lecture 2 Notes

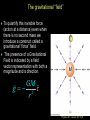
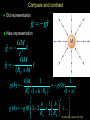
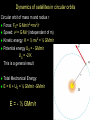
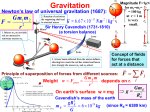
Lecture 25
Jupiter and 4 of its moons
under the influence of
gravity
Goal: To use Newton’s
theory of gravity to analyze
the motion of satellites and
planets.
Physics 201: Lecture 25, Pg 1
Exam results
Mean/Median 59/100
 Nominal exam curve
A 81-100
AB 71-80
B 61-70
BC 51-60
C 31-50
D 25-30
F below 25

Physics 201: Lecture 25, Pg 2
Newton’s Universal “Law” of Gravity
Newton proposed that every object in the universe attracts every
other object.
The Law: Any pair of objects in the Universe attract each other
with a force that is proportional to the products of their masses
and inversely proportional to the square of their distance
Physics 201: Lecture 25, Pg 3
Newton’s Universal “Law” of Gravity


m1m2
Fon 2 by 1  G 2 r̂12   Fon1by 2
r
“Big” G is the Universal Gravitational Constant
G = 6.673 x 10-11 Nm2 / kg2
Two 1 Kg particles, 1 meter away  Fg= 6.67 x 10-11 N
(About 39 orders of magnitude weaker than the electromagnetic
force.)
The force points along the line connecting the two objects.
Physics 201: Lecture 25, Pg 4
Little g and Big G
Suppose an object of mass m is on the surface of a
planet of mass M and radius R. The local gravitational
force may be written as
FG  mg surface
where we have used a local constant acceleration:

mGM
Fon m by M  
r̂M ,m
2
R
GM On Earth, near sea level, it can
g surface  2
be shown that gsurface ≈ 9.8 m/s2.
R
Physics 201: Lecture 25, Pg 5
g varies with altitude

With respect to the Earth’s surface
g (h)  GM E /( RE  h)
2
Physics 201: Lecture 25, Pg 6
At what distance are the Earth’s and moon’s
gravitational forces equal



Earth to moon distance = 3.8 x 108 m
Earth’s mass = 6.0 x 1024 kg
Moon’s mass = 7.4 x 1022 kg
GM E / r  GM M / r
2
E
2
M
r / r  MM / ME
2
M
2
E
rM / rE  M M / M E  0.11
rM  rE  3.8 10 m
8
rE  3.8 10 m/1.11  3.4 10 m
8
8
Physics 201: Lecture 25, Pg 7
The gravitational “field”


To quantify this invisible force
(action at a distance) even when
there is no second mass we
introduce a construct called a
gravitational “force” field.
The presence of a Gravitational
Field is indicated by a field
vector representation with both a
magnitude and a direction.
M
GM

g   2 r̂
r
Physics 201: Lecture 25, Pg 8
Compare and contrast

Old representation

New representation

g   gr̂
GM

g   2 r̂
r
GM

g
r̂
2
( RE  h)
M
GM
1
1
g ( h)   2
  g (0)
2
RE (1  h / RE )
(1  x) 2
2


h 3 h 
g (h)   g (0) 1  2
    ...
RE 2  RE  Physics 201:

 Lecture 25, Pg 9
Gravitational Potential Energy
Recall for 1D:
F ( x)  dU ( x) / dx
W  xx F ( x)  dx
f
i
W
rf
ri

Gm1m2 Gm1m2

1
FG  dr ( r ) 

rf
ri
2
When two isolated masses m1 and m2 interact over large
distances, they have a gravitational potential energy of
U (r )  Gm1m2 / r
The “zero” of potential energy occurs at r = ∞, where the force
goes to zero.
Note that this equation gives the potential energy of masses m1
and m2 when their centers are separated by a distance r.
Physics 201: Lecture 25, Pg 10
A plot of the gravitational potential energy
U (r )  Gm1m2 / r
Ug= 0 at r = ∞
 We use infinity as reference
point for Ug(∞)= 0
 This very different than
 U(r) = mg(r-r0)
 Referencing infinity has
some clear advantages
 All r allow for stable orbits
but if the total mechanical
energy, K+ U > 0, then the
object will “escape”.

Physics 201: Lecture 25, Pg 11
It is the same physics

Shifting the reference point to RE.
GmM E
U ( RE  h)  
RE  h
GmM E GmM E
U ( RE  h)  U ( RE )  

RE  h
RE

RE
( RE  h) 
 Gm1m2 


R
(
R

h
)
R
(
R

h
)
 E E

E
E

 GmM E
h
 GmM E  2

h
2

RE
 RE  RE h 
GM E
m 2 h  mgh
RE
Physics 201: Lecture 25, Pg 12
Gravitational Potential Energy with many masses

If there are multiple particles
U Total  U12  U13  U 23
 m1m2
m1m3
m2 m3 
U (r )  G         
 | r1  r2 | | r1  r3 | | r2  r3 | 

Neglects the potential
energy of the many
mass elements that
make up m1, m2 & m3
(aka the “self energy”
Physics 201: Lecture 25, Pg 13
Dynamics of satellites in circular orbits
Circular orbit of mass m and radius r
 Force: FG= G Mm/r2 =mv2/r
 Speed: v2 = G M/r (independent of m)
 Kinetic energy: K = ½ mv2 = ½ GMm/r
 Potential energy UG = - GMm/r
UG = -2 K
This is a general result


Total Mechanical Energy:
E = K + UG = ½ GMm/r -GMm/r
E = - ½ GMm/r
Physics 201: Lecture 25, Pg 14
Changing orbits
With man-made objects we need to change the orbit
Examples:
1. Low Earth orbit to geosynchronous orbit
2. Achieve escape velocity
 1. We must increase the potential energy but one can
decrease the kinetic energy consistent with

U G (r )  
GMm
r
GMm
K (r )   U G (r ) 
2r
1
2
GMm
E (r )  U G (r )  K (r )  
2r
Physics 201: Lecture 25, Pg 15
Changing orbits

Low Earth orbit to geosynchronous orbit
GMm
E (r )  U G (r )  K (r )  
2r


A 470 kg satellite, initially at a low Earth orbit of hi = 280 km
is to be boosted to geosynchronous orbit hf = 35800 km
What is the minimum energy required to do so?
(rE = 6400 km, M = 6 x 1024 kg
 1 1 

E  E (rf )  E (ri )  GMm


2
r
2
r
i 
 f
1
 1

11
24
E  6.67 10 (6 10 )470

/2
7
6 
 4.2 10 6.7 10 
10
E  1.2 10 J
Physics 201: Lecture 25, Pg 16
Escaping Earth orbit

Exercise: suppose an object of mass m is
projected vertically upwards from the
Earth’s surface at an initial speed v, how
high can it go ? (Ignore Earth’s rotation)
Ei  U G ( RE )  mv
1
2
2
i
E f  U G ( RE  h)  0
E f  Ei  U G ( RE  h)  0
 GmM /( RE  h)  GmM / RE  mv
2
1
 1 /( RE  h)  1/ RE  2 mvi /(GmM )
1
2
2
i
Physics 201: Lecture 25, Pg 17
Escaping Earth orbit

Exercise: suppose an object of mass m is
projected vertically upwards from the
Earth’s surface at an initial speed v, how
high can it go ? (Ignore Earth’s rotation)
 1 /( RE  h)  1 / RE  12 mvi2 /(GmM )
h  ( R  hRE )v /(2GM )
2
E
2
i
h(1  R v /(2GM ))  R v /(2GM )
2
E i
2 2
E i
2 2
E i
Rv
h
2
(2GM  RE vi )
Physics 201: Lecture 25, Pg 18
Escaping Earth orbit

Exercise: suppose an object of mass m is
projected vertically upwards from the
Earth’s surface at an initial speed v, how
high can it go ? (Ignore Earth’s rotation)
2 2
E i
Rv
h
2
(2GM  RE vi )
2GM  RE vi2  0
vEscape
implies infinite height
2GM

 11.2 km/s
RE
Physics 201: Lecture 25, Pg 19
Some interesting numbers
First Astronautical Speed
 Low Earth orbit:
v = 7.9 km/s
 Second Astronautical Speed
 Escaping the Earth:
v = 11 km/s
 Third Astronautical Speed
 Escaping Solar system: v= 42 km/s

Physics 201: Lecture 25, Pg 20
Next time

Chapter 14 sections 1 to 3, Fluids
Physics 201: Lecture 25, Pg 21