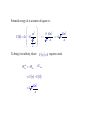* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Q08._Gravity-Ans
Survey
Document related concepts
Transcript
Q08. Gravity 1. Suppose you have a pendulum clock which keeps correct time on Earth (acceleration due to gravity = 9.8 m/s2). Without changing the clock, you take it to the Moon (acceleration due to gravity = 1.6 m/s2). For every hour interval (on Earth) the Moon clock will record: 1. (9.8/1.6) h 2. 1h 3. 9.8 / 1.6 h 4. (1.6/9.8) h 5. 1.6 / 9.8 h 2. The mass density of a certain planet has spherical symmetry but varies in such a way that the mass inside every spherical surface with center at the center of the planet is proportional to the radius of the surface. If r is the distance from the center of the planet to a point mass inside the planet, the gravitational force on the mass is : 1. not dependent on r 2. proportional to r2 3. proportional to r 4. proportional to 1/ r 5. proportional to 1/ r2 Mass inside radius R : M R r 4 r d r R R 2 0 1 r2 Force due to mass shell beyond m vanishes. Force due to mass sphere beneath m is the same as if it’s a point mass M(r) placed at the center. m M r f G r2 r 1 r2 r 3. Each of the four corners of a square with edge a is occupied by a point mass m. There is a fifth mass, also m, at the center of the square. To remove the mass from the center to a point far away the work that must be done by an external agent is given by : 1. 4Gm2/a 2. –4Gm2/a 3. (42) Gm2/a 4. –(42) Gm2/a 5. 4Gm2/a2 Potential energy of m at center of square is : m2 U 0 4 G 2 a 2 U 0 requires work To bring it to infinity, where W0ext W0 8 Gm 2 Gm 2 4 2 a 2 a U0 U U 0 Gm 2 4 2 a 4. A projectile is fired straight upward from Earth's surface with a speed that is half the escape speed. If R is the radius of Earth, the highest altitude reached, measured from the surface, is 1. R/4 2. R/3 3. R/2 4. R 5. 2R 1 v K m esc 2 2 By definition: 2 1 2 M vesc G E 2 R Maximum height H is given by: E K U R U R H 1 v K m esc 2 2 2 1 1 GmM E RH R 1 1 1 4R R R H H R 3 1 3 R H 4R ( Energy conservation ) 5. An object is dropped from an altitude of one Earth radius above Earth's surface. If M is the mass of Earth and R is its radius the speed of the object just before it hits Earth is given by : 1. GM / R 2. GM / 2R 3. 2GM / R 4. GM / R 2 5. GM / 2 R 2 Energy conservation : E U 2R K U R 1 2 1 1 mv GmM 2 2R R v GM R 1 GmM 2 R 6. A planet in another solar system orbits a star with a mass of 4.0 1030 kg. At one point in its orbit it is 250 106 km from the star and is moving at 35 km/s. Take the universal gravitational constant to be 6.67 10–11 m2/s2 kg and calculate the semimajor axis of the planet's orbit. The result is : 1. 79 106 km 2. 160 106 km 3. 290 106 km 4. 320 106 km 5. 590 106 km Energy conservation : 30 1 4.0 10 2 3 11 E K U M 35 10 6.67 10 9 2 250 10 4.547 108 M Using E G M MS 2a ( M = mass of planet ) ( MS = mass of star, a = semimajor axis ) , we have 6.67 10 4.0 10 a 2 4.547 10 11 30 8 2.93 1011 m 290 106 km 7. A spaceship is returning to Earth with its engine turned off. Consider only the gravitational field of Earth and let M be the mass of Earth, m be the mass of the spaceship, and R be the distance from the center of Earth. In moving from position 1 to position 2 the kinetic energy of the spaceship increases by : 1. 2. 3. 4. 5. 1 1 GMm 2 2 R 2 R1 1 1 GMm 2 2 R1 R 2 R R GMm 1 2 22 R1 R 2 R1 R2 GMm R1 R2 GMm R 2 R1 R1 R2 Energy conservation : E K1 U1 K2 U 2 K2 K1 U1 U 2 1 1 GMm R1 R2 R1 R2 GMm R R 1 2