* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Spiral arms in the milky way galaxy and cosmic rays
Survey
Document related concepts
Transcript
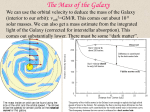
Spiral arms in the milky way galaxy and cosmic rays Smadar Levi The Hebrew University of Jerusalem International School of Cosmic Ray Astrophysics July 2004 Work in progress in collaboration with Nir Shaviv A typical galaxy ~15Kpc ~0.5Kpc The disk The Central Bulge The disk is characterized with stars that move in nearly circular orbits around the galactic center. The Central Bulge is characterized with stars with large random motions. Therefore its distribution is ellipsoidal. The star in the disk has a differential velocity, meaning the star nearer to the center has a shorter period of motion. Density Waves The Lin Shu Hypothesis • Spiral structure is: Quasi – steady density wave. • The arms are a region where the star density is the highest. • The Star velocity is different than the arms velocity. • The spiral arms represent the places where the stars spend more time than in an equivalent area of space elsewhere in the galaxy. Spiral wave – the moving traffic jam Stars=cars spiral arm=jam t1 t2 t3 Direction of movement Finding the arms velocity We wish to work in a frame of reference which rotates with the arms. And P We denote as the circular velocity of the stars. is the circular velocity of the arms, which we call: pattern speed . birth r P t is the measured angle At first we simplify the analysis by assuming that the orbits are circular. Hence: rbirth r Analysis • Open clusters. From Loktin & Dias catalogs. • Fitting the data to a logarithmic arm with 500pc thickness. rarm e abirth b • 3 parameters to find. • a – the slope. • b – the interjection point with the r axis. • P - the pattern speed Analysis Analysis • Fitting 500pc logarithmic arm to the data points: Finding a minimum to a weight function. 1 rarm ~ 500 pc 1 rarm r d • Bootstrap: Replacing ~37% random data points by ~37% different random points. • Extracting the Bootstrap: significant minima's The term derives from the phrase and finding the errors. to pull oneself up by one's bootstraps (Adventures of Baron Munchausen, by Rudolph Erich Raspe). Looking for minimum Two sets of arms!! In The Milky Way .... Two sets of arms!! for : r 8.5kpc V 240 km sec km Pkm 14.2 0.7 km P 14.2 0.7 P sec 30 .4 0.5 kpc sec kpc sec kpc Every ~125 million years Nir Shaviv [2003] higher CR flux future work: ? Improving the position limits Density profile ice age














![Epicycles… the short form. For lurid details, see [CO pp.1018-1030] φ](http://s1.studyres.com/store/data/008843298_1-98c16174ecb2a061ac002b14bc07a0da-150x150.png)






