* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Review 3 - Physics and Astronomy
Spitzer Space Telescope wikipedia , lookup
Corvus (constellation) wikipedia , lookup
Astrophotography wikipedia , lookup
Theoretical astronomy wikipedia , lookup
Aquarius (constellation) wikipedia , lookup
Modified Newtonian dynamics wikipedia , lookup
Hubble Deep Field wikipedia , lookup
Star formation wikipedia , lookup
First observation of gravitational waves wikipedia , lookup
Dialogue Concerning the Two Chief World Systems wikipedia , lookup
International Ultraviolet Explorer wikipedia , lookup
Malmquist bias wikipedia , lookup
Timeline of astronomy wikipedia , lookup
Astronomical unit wikipedia , lookup
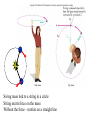
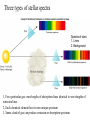
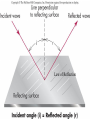
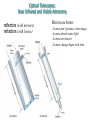
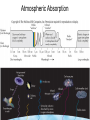
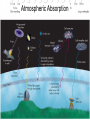
Astronomical Motion Basics terms and concepts Force: action that changes the state of motion of an object. Inertia: the resistance of an object to the change of its state of motion. "mass" has two meanings: • amount of matter • measure of inertia (more massive bodies are more inert) Speed, Velocity and Acceleration • Speed is a scalar quantity which refers to "how fast an object is moving." • 50 mi/h – Instantaneous speed: the speed in an instant – Average speed = total distance covered / duration of travel • Velocity is a vector quantity which refers to "how fast an object is moving and to where.“ • 50 mi/h to the North • Acceleration – how does the velocity change The Second Law of Newton: a = F/m, or F = ma Force a m Acceleration: the rate of change of velocity - speeding up, slowing down, or changing direction of motion "The acceleration of an object is proportional to the net force on it and inversely proportional to its mass". The bigger the force, the bigger the acceleration. The bigger the mass the smaller the acceleration. Swing mass tied to a string in a circle String exerts force on the mass Without the force – motion on a straight line Universal Gravitational Force Every two masses, M and m, attract each other with a force proportional to them, and inversely proportional to the square of the distance between them: M m d Mm F G 2 d G is the gravitational constant, measured experimentally, G=6.67x10-11 Nm2/kg2 Key Ideas •Kepler’s Laws •P 2 = a3 •Newton’s Laws • Speed, velocity, acceleration, force, inertia, mass, balanced and unbalanced forces • F= ma •Law of Universal Gravitation Mm F G 2 d Kepler’s Laws reconsidered Newton’s version of the Kepler’s 3rd empirical law: 4 a P G(m M ) 2 3 2 M m a P Units: P - in seconds, a - in meters. Allows to calculate masses Newton figured out that the gravitational attraction between two objects is given by: mm F G 12 2 r where F is the force of attraction, G is a constant, m1 and m2 are the masses of the two objects, and r is the distance between them. If we increase the mass of the first object twice, the force will become a. 32 times weaker b. 8 times weaker c. 2 times stronger d. 8 times stronger e. none of the above is correct Light Basics How does light travel? fast & straight: 300,000 km/s Macroscopic Properties of Light reflected refracted blocked absorbed and re-emitted Nature of Light electromagnetic wave particle (photon) Properties of Waves Frequency = 1/Period : f = 1/T Wave pulse wave f is measured in 1/sec, or Hz Velocity = wavelength x frequency: v = lf Velocity is measured in m/s Light wave in vacuum : c = 300 000 km/s = lf Huge range in l and f c = lf always!!! Amplitude A tsunami, an ocean wave generated by an earthquake, propagates along the open ocean at 700 km/hr and has a wavelength of 750 km. What is the frequency of the waves in such a tsunami? A) 0.933 Hz B) 0.000259 Hz C) 1.07 Hz D) 0.148 Hz Answer: B Examples of Mechanical Waves Need a medium to propagate Water waves tuning fork: vibrating object can produce sound Waves in a Guitar String Pressure waves Light is a special kind of wave Oscillating electric charges (for example, in antennas) => produce changing magnetic field => which produces changing electric field => which produce changing magnetic field, and so on… Fig.06.05 Types EM waves c = lf White Light Made up of all wavelengths Fig. 16.9 Energy Levels for the Hydrogen atom and possible emission lines Small change in energy – redder color Spectrum Radiation of different wavelength and frequency is obtained The “Fingerprint” of Different Elements Each element has its own family of unique spectral lines. Three types of stellar spectra Spectra of stars 1. Lines 2. Background 1. For a particular gas: wavelengths of absorption-lines identical to wavelengths of emission lines 2. Each chemical element has its own unique spectrum 3. Same cloud of gas can produce emission or absorption spectrum Different stars – different spectra Fig. 7.61. Wien’s law 0.0029 lmax (m) T (K ) 2. Stefan – Boltzmann law E T 4 T (heat) ~ random motion of particles Doppler Effect λ ~ 550 nm Source of light receding from us at high speed Slide 21 λ ~ 600 nm Doppler Effect • Christian Johann Doppler (1803-1853) • Information about the motion of the object • Calculating the Doppler Shift – Normal wavelength – Source approaching the observer: waves bunched up ahead of it – λ decreases – Source receding from the observer: waves are stretched out – λ increases shifted wavelength real wavelength speed of object speed of light real wavelength Refraction Reflection Law of Reflection The optical effect of refraction Speed of light different in different materials Vacuum – c =300 000 km/s Material – v < c Less dense to more dense – bands toward the normal line Index of refraction c/v = n >1 Optical Telescopes: Near Infrared and Visible Astronomy reflectors (with mirrors) refractors (with lenses) Mirrors are better: - Lenses don’t produce clear image - Lenses absorb some light - Lenses are heavier - Lenses change shape with time What is important for a telescope? •Diameter of the objective mirror (lens) • Light-gathering power power ~ diameter 2 •Angular resolution (in arcsec): •The Focal Lengths • Magnification wavelength resolution ~ 250,000 diameter fo m fe Yerkes Observatory Atmospheric Absorption Atmospheric Absorption Astronomy at radio-wavelengths • Earth’s atmosphere largely transparent • Can penetrate dusty regions of interstellar space • Observations in daytime as well as at night • High resolution requires large telescopes Surface of planets (Venus) Planetary magnetic fields Structure of Milky Way and other galaxies Cosmic Background Radiation The 64 meter radio telescope at Parkes Observatory, Australia Fig.06.40 Arecibo Observatory, Puerto Rico Constructed in natural limestone bedrock The very large array (VLA) Central New Mexico 27 independent radio dishes, 25m each, spread over large distance Better resolution Near Infrared and Visible Astronomy •Earth’s atmosphere transparent to visible light, but only partly to IR light •Near IR can penetrate dusty regions of interstellar space •Surface of planets •Physical Properties of Stars •Structure of Milky Way, other galaxies and the Universe •Other Solar Systems •Searching for the first stars and galaxies Existing Large Optical Telescopes 1.5-m 2.5-m 5.0-m 6.5-m 10-m Mt Wilson Mt Wilson Mt Palomar Russia Keck, Mauna Kea, Hawaii 8.2-m VLT, ESO, Chile Many 3 – 3.5 m telescopes Several 6-6.5 m telescopes One of the two Keck telescopes Fig.06.26 Fig.06.35 Exploring Other Solar Systems Very difficult to see small planets Need superb resolution 200 giant planets 1 rocky planet 'Super Earth' Discovered at Nearby Star “OverWhelmingly Large telescope” ~ 25 Earths At the visual range we will be able to distinguish between 2 stars 0.001 arcsec apart Ultraviolet, X-ray, Gamma-ray and Far IR Astronomy •Observations must be made from space •UV and X-ray: special mirror configurations needed to form images •Gamma-rays cannot form images Stellar structure and evolution Structure of Milky Way and other galaxies Fig.06.34 Mauna Kea Observatory, Hawaii Cerro Tololo Inter-American Observatory Fig.06.33 Basic Properties of Stars Stellar parallax 1. Apparent change in the position of a star caused by the motion of the Earth around the Sun. 2. Detecting parallaxes means that Earth orbits around Sun 3. Maximum parallactic shift (two positions of the Earth’s orbit 6 months apart) Earth in December Figure 2 1 b A 2 Earth in November Earth in July d B 3 1 d pc parc sec A simple relationship (often called parallax-distance formula) between distance in parsecs and stellar parallax in arcseconds Proxima Centauri: distance : 4.3 LY = 4.3/3.26 pc = 1.3 pc parallax : 0.76 arcsec Luminosity depends on temperature and size Luminosity ~ T4R2 Measure of true stellar brightness Luminosity • the total amount of energy a star radiates out into space each second •Tells us how much energy is being generated within the star •Amount of generated energy is different for different stellar types !!! Same distance to both !!! !!! Same distance to both !!! Apparent brightness Real Sky: • • • • Stars of different size and color (different luminosity) Different distances Energy reaching us depends on distance, T, R Apparent brightness - the true brightness affected by distance Far away Nearby Need to know stellar distances! The brightness of the source of light decrease as we recede from it. • Imagine an observer located at a distance d from a 150 Watt light bulb. Let’s call the brightness of this bulb, as seen by this observer, B. When the observer recedes from the bulb, the brightness B drops off as the square of the distance d. The brightness B and the distance d are related as 150 B 2 4d Inverse-square dependence Apparent brightness, true brightness, distance, magnitude scale • Apparent brightness – 6 groups of visible star • brightest - 1st magnitude • faintest - 6th magnitude – Apparent brightness and apparent mag m – An increase of 1 mag corresponds to a decrease in brightness by a factor of ~2.5 times – An increase of 5 mag corresponds to a decrease in brightness of 100 times • True brightness – All stars artificially moved at distance from Earth 10 pc: – Intrinsic brightness (luminosity) and absolute mag M • m -M = 5 log (d / 10)