* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Production and Decay of Hadronic Resonances after
Eigenstate thermalization hypothesis wikipedia , lookup
Compact Muon Solenoid wikipedia , lookup
Standard Model wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
Wave packet wikipedia , lookup
Elementary particle wikipedia , lookup
Relativistic quantum mechanics wikipedia , lookup
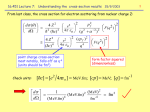
Enhancement of hadronic resonances in RHI collisions Inga Kuznetsova and Johann Rafelski Department of Physics, University of Arizona We explain the relatively high yield of charged Σ±(1385) reported by STAR We show if we have initial hadrons multiplicity above equilibrium the fractional yield of resonances A*/A (A*→Aπ) can be considerably higher than expected in SHM model of QGP hadronization. We study how non-equilibrium initial conditions after QGP hadronization influence the yield of resonances. Work supported by a grant from: the U.S. Department of Energy DE-FG02-04ER4131 Time evolution equation for NΔ, NΣ Δ(1232) ↔ Nπ, width Γ≈120 MeV (from PDG); Σ(1385)↔Λπ ,width Γ ≈ 35 MeV (from PDG). Reactions are relatively fast. We assume that others reactions don’t have influence on Δ (Σ) multiplicity. 1 dN dWN dW N V dt dtdV dtdV dW N dVdt dWN and are Lorentz invariant rates dVdt Phases of RHI collision QGP phase; Chemical freeze-out (QGP hadronization); We consider hadronic gas phase between chemical freeze- out (QGP hadronization) and kinetic freeze-out; the hadrons yields can be changed because of their interactions; M. Bleicher and J.Aichelin, Phys. Lett. B, 530 (2002) 81 M. Bleicher and H.Stoecker,J.Phys.G, 30, S111 (2004) Kinetic freeze-out : reactions between hadrons stop; Hadrons expand freely (without interactions). Motivations How resonance yield depends on the difference between chemical freeze-out temperature (QGP hadronization temperature) and kinetic freezeout temperature? How this yield depends on degree of initial nonequilibrium? Explain yields ratios observed in experiment . Distribution functions 1 f 1 ; exp( u p ) 1 1 f i 1 , i N , , , i exp( u pi ) 1 u pi Ei for u (1,0) in the rest frame of heat bath 3 Multiplicity of resonance: T 2 N i i 2 gi xi K 2 xi V 2 where xi=mi /T; K2(x) is Bessel function; gi is particle i degeneracy; Υi is particle fugacity, i = N, Δ, Σ, Λ; Equations for Lorentz invariant rates dW N g d 3 p d 3 pN d 3 p f 3 3 3 dtdV (2 ) 2 E 2 E N (2 ) 2 E (2 ) 1 (2 ) ( pN p p ) g 4 p M pN p 2 (1 f N )(1 f ) spin dWN g N g d 3 p d 3 pN d 3 p f f 3 3 N 3 dtdV (2 ) 2 E 2 EN (2 ) 2 E (2 ) 1 (2 ) ( pN p p ) g N g 4 spin 2 pN p M p (1 f ) Bose enhancement factor: f 1 1 exp( u p ) f 1 f 1 Fermi blocking factor: i i exp( u pi ) f i using energy conservation and time reversal symmetry: spin pN p M p 2 p M pN p spin dW N dWN we obtained: N dtdV dtdV 1 dN dWN dW N V dt dtdV dtdV 2 We obtained: dWN dN N 1 dt dtdV I. Kuznetsova, T. Kodama and J. Rafelski, ``Chemical Equilibration Involving Decaying Particles at Finite Temperature '' in preparation. Equilibrium condition: N 1 If in initial state 0 eq N eq is global chemical equilibrium. 0 N 0 If in initial state 0 eq 0 N 0 then Δ production is dominant. then Δ decay is dominant. We don’t know decay rate, we know decay width or decay time in vacuum τΔvac =1/Γ. We can write time evolution equation as N dN N 1 dt 1 dN dW N where is decay time in medium V d dtdV N For Boltzmann distributions: V We assume that no medium effects, τΔ≈τΔvac dW N dtdV Model assumptions Δ(1232) ↔ N π is fast. Other reactions do not influence Δ yield or N NN N N N 0 0 N tot 0 const The same for Σ(1385)↔Λπ N N N N const 0 0 tot 0 Large multiplicity of pions does not change in reactions Most entropy is in pions and entropy is conserved during expansion of hadrons as dS 3 dV T const. dy dy Equation for ΥΔ(Σ) 1 dN 1 d d ln( x2 K2 ( x )) dT 1 d (VT 3 ) x m 3 , T N d d dT d VT d d 1 1 1 N d T S τ is time in fluid element comoving frame. d ln( x2 K2 ( x )) dT , T dT d 1 d ln( VT 3 ) 0 S d 1 Expansion of hadronic phase Growth of transverse dimension: R ( ) R0 v( )d 0 v( ) vmax arctan( 4( 0 ) / r ) is expansion velocity dV 3 2 dz 3 2 T T R T R const Taking dy dy dT 1 2( v / R ) 1 we obtain: Td 3 3 At hadronization time τh: 0.5 m 1 0.7 m h T T h T Solution for ΥΔ Using particles number conservation: Δ + N = N0tot we obtain equation : d ~ q( ), d N 1 1 ~ where ( ) 1 , NN T N 0tot 1 q( ) . NN The solution of equation is: ~ ~ 0 ( ) q exp d d exp d h h h Non-equilibrium QGP hadronization γq is light quark fugacity after hadronization q ; q ; 0 N 3 0 Entropy conservation s q ; 2 0 3 q ; 0 2 dS QGP dS HG fixes γ (≠1). q dy dy s q ; 0 2 Strangeness conservation fixes γs (≠1). γq is between 1.6 for T=140 MeV and 1 for T=180 MeV; Initially 0( ) N0 ( ) 0 and Δ (Σ) production is dominant Temperature as a function of time τ The ratios NΔ/NΔ0, NN/NN0 as a function of T NΔ increases during expansion after hadronization when γq>1 (ΥΔ < ΥNΥπ) until it reaches equilibrium. After that it decreases (delta decays) because of expansion. Opposite situation is with NN. If γq =1, there is no Δ enhancement, Δ only decays with expansion. NΔ/Ntot ratio as a function of T. Ntot (observable) is total multiplicity of resonances which decay to N. Dot-dashed line is if we have only QGP freeze-out. Doted line (SHARE) is similar to dot-dashed line with more precise decays consideration. There is strong dependence of resulting ratio on hadronization temperature. NΣ/Λtot ratio as a function of T Observable: tot (1385) 0 (1193) Y * Effect is smaller than for Δ because of smaller decay width Experiment: (1385) (1385) 0.29 tot tot (1385) 3 (1385) (1385) tot 2 tot tot J.Adams et al. Phys.Rev. Lett. 97, 132301 (2006) S.Salur, J.Phys.G, 32, S469 (2006) Future study Γ≈ 150 MeV; K * (892) K Γ≈50 MeV K1 (1400) K * (892) Γ≈170 MeV Conclusions If we have initial hadrons multiplicity above equilibrium the fractional yield of resonances A*/A can be considerably higher than expected in SHM model of QGP hadronization. Because of relatively strong temperature dependence, Δ/Ntot can be used as a tool to distinguish the different hadronization conditions as chemical non-equilibrium vs chemical equilibrium; We have shown that the relatively high yield of charged Σ±(1385) reported by STAR is well explained by our considerations and hadronization at T=140 MeV is favored.