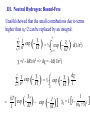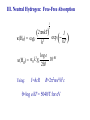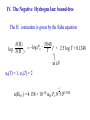Download Spectroscopy – Lecture 1

Spectroscopy – Continuous Opacities
I. Introduction: Atomic Absorption Coefficents
II. Corrections for Stimulated Emission
III. Hydrogen
IV. Negative Hydrogen Ion
V. Negative Helium Ion
VI. Metals
VII. Electron Scattering
VIII. Others
IX. Summary
In order to calculate the transer of radiation through
a model stellar atmosphere, we need to know the
continuous absorption coefficient, kn.
This shapes the continous spectrum → more
absorption, less light.
It also influences the strength of stellar lines →
more continous absorption means a thinner
photosphere with few atoms to make spectral lines.
Also, before we compute a theoretical spectrum, you
need to compute an atmospheric model, and this
also depends on kn.
Recall the radiative transfer equation:
dIn
= –In + jn/kn = –In + Sn
dtn
To solve this you need to know the opacity. You
can have a nice solution, but it will not reproduce
observations. The grey atmosphere has a simple
opacity, but no bearing with reality.
The problem is that there are a lot of opacity
sources which are temperature dependent
B1I V
F0 V
G2 V
I. The atomic absorption coefficent
The total continuous absorption coefficient is the
sum of absorption resulting from many physical
processes. These are in two categories:
• bound-free transition: ionization
• free-free transition: acceleration of a charge when
passing another charge
bound-bound transitions result in a spectral line and
are not included in kn but in cool stars line density is
so great it affects the continuum
I. The atomic absorption coefficent
The atomic absorption coefficient, a, has units of
area per absorber.
The wavelength versus frequency question does not
arise for a:
an = al
a is not a distribution like In and Il, but the power
subtracted from In in interval dn is adn. This is a
distribution and has units of erg/(s cm2 rad2 Hz)
a dn =(c/l2) a dl
II. Corrections for Stimulated Emission
Recall that the stimulated emission (negative
absorption) reduces the absorption:
knr = NℓBℓuhn – NuBuℓhn
= Nℓ Bℓuhn(1– NuBuℓ/NℓBℓu)
= NℓBℓuhn[1– exp(–hn/kT)]
Nu
Blu
Nℓ
Bul
lT cm K
T
0.2
0.4
0.6
0.8
1.0
4000
8000
12000
16000
20000
Teff
30000
3000
1– exp(hn/kT) % decrease
0.999
0.973
0.909
0.834
0.763
l (10% reduction)
2500 Ang
2mm
0.08
2.8
10.0
19.8
31.1
13.60
12.75
12.08
Brackett
Pachen
Balmer
Lyman
III. Atomic Absorption Coefficient for Hydrogen
½ mv2 = hn–hRc/n2
R = 1.0968×105 cm–1
··
n=∞
n=4
n=3
Ha b
10.20
0.00
c = 13.6(1–1/n2) eV
n=2
n=1
½ mv2 = hn–hRc/n2
R = 1.0968×105 cm–1
At the ionization limit v=0, n=Rc/n2
Absorption edges:
n
l Ang
1
912
Lyman
2
3647
Balmer
3
8206
Paschen
4
14588
Brackett
5
22790
Pfund
Name
III. Neutral Hydrogen: Bound-Free
Original derivation is from Kramers (1923) and
modified by Gaunt (1930):
pe6 R g ∕
an = 6.16
n
5
3
h nn
an = 6.16
p2e6
h3c3
R
l3
Per neutral H atom
gn∕ =
a0 gn∕ l3
n5
n5
a0 = 1.044×10–26 for l in angstroms
e = electron charge = 4.803×10–10 esu
gn∕ = Gaunt factor needed to make Kramer´s result in agreement
with quantum mechanical results
n =1
n =2
n =3
n=4
n=5
a0, 10×–17 cm2/H atom
n=6
~l3/n5
Wavelength (Angstroms)
~l3
n=7
III. Neutral Hydrogen: Bound-Free
The sum of absorbers in each level times an
is what is needed.
Recall:
Nn
N
gn
c
exp –
=
u0(T)
kT
(
)
gn=2n2
u0(T) = 2
c =I – hRc/n2 = 13.6(1-1/n2) eV
III. Neutral Hydrogen: Bound-Free
The absorption coefficient in square centimeters per
neutral hydrogen atom for all continua starting at n0
∞
k(Hbf) = Σ
n
0
anNn
N
= a0
= a0
∞
Σ
n0
∞
Σ
n0
l3 ∕
c
g
n3 n exp – kT
(
l3 ∕
gn 10–qc
3
n
q = 5040/T, c in electron volts
)
III. Neutral Hydrogen: Bound-Free
Unsöld showed that the small contributions due to terms
higher than n0+2 can be replaced by an integral:
∞
Σ
n0+3
1 exp – c
n3
kT
(
)
∞
c
= ½ ∫ exp –
kT
n +3
(
0
)
d(1/n2)
c =I – hRc/n2 => dc = –Id(1/n2)
∞
Σ
n0+3
=
1 exp – c
n3
kT
(
kT exp – c3
[
kT
I
( )–
I
) = ½∫
c3
exp
c
exp –
kT
I
(
(– kT) ]
)
dc
I
1
c3 = I [1– (n +3)2 ]
0
III. Neutral Hydrogen: Bound-Free
We can neglect the n dependence on gn∕ and the final
answer is:
k(Hbf) = a0l3
n0+2
[Σ
n0
gn∕ –qc log e
–c q
–Iq)
(10
–
10
+
3
]
2qI
n3 10
This is the bound free absorption coefficient for
neutral hydrogen
n =1
n =2
n =3
n=4
n=5
n=6
n=7
III. Neutral Hydrogen: Bound-Free
=
kbf(n=3) + ...
kbf(n=2) + kbf(n=3) + ...
≈
kbf(n=3)
kbf(n=2)
8
= 27 exp [ –(c3 – c2)/kT
[
kbf(>3647)
kbf(<3647)
= 0.0037 at 5000 K and 0.033 at 10000 K
III. Neutral Hydrogen: Bound-Free
k(red side)/k(blue side)
l edge
(Ang)
T
3000
T
5000
T
10000
T
30000
Lyman
912
9×10–19
6×10–12
9×10–7 0.002
Balmer
3647
0.00021
0.00376
0.033
0.14
Paschen 8206
0.03
0.089
0.177
0.31
Brackett 14588
0.16
0.255
0.36
0.45
Pfund
0.30
0.39
0.48
0.54
22790
III. Neutral Hydrogen: Bound-Free
III. Optical Depth and Height of Formation
3647
8602
continuum
Flux
912
Across a jump
your are seeing
very different
heights in the
atmosphere
Wavelength
Recall: tn = knrdx
tn ~ 2/3 for Grey atmosphere
As an increases, kn increases => dx decreases
You are looking higher in the atmosphere
Temperature profile
of photosphere
Temperature
k(<3647) > k(>3647) =>
dx2 > dx1
l<3647 A
l>3647 A
10000
8000
6000
4000
z=0
z
z=0
dx1
dx2
t=2/3
t=2/3
z
B4 V
But wait, I just said that the Balmer jump should be larger for cooler
stars. Why is this not the case?
For cooler stars other sources of opacity start to dominate, namely H–
Maximum of black body = lT = 0.5099 cm K
But peak implies T=13400 K
But peak implies T=13400 K
The stronger opacity of on the blue side of the Balmer jump distorts the
Planck curve. One cannot use the peak of the intensity, but must fit the full
spectral energy distribution
Amplitude (mmag)
Photometric Amplitude of rapidly oscillating Ap stars:
Wavelength (Ang)
Different wavelengths probe different heights in atmosphere
III. Neutral Hydrogen: Free-Free
The free-free absorption of hydrogen is much
smaller.
When the free electron has a collision with a
proton its unbound orbit is altered.
The electron can absorbs a photon and its energy
increases.
The strength of this absorption depends on the
velocity of the electron
III. Neutral Hydrogen: Free-Free
proton
e–
Orbit is altered
The absorption of the photon is during the
interaction
III. Neutral Hydrogen: Free-Free Absorption
According to Kramers the atomic coefficient is:
daff
h2e2 R 1
= 0.385
pm3 n3 v dv
This is the cross section in square cm per H atom for
the fraction of the electrons in the velocity interval v
to v + dv.
To get complete f-f absorption must integrate over v.
III. Neutral Hydrogen: Free-Free Absorption
Using the Maxwell-Boltzmann distribution for v
h2e2 R 1
aff = 0.385
pm3 n3
∞
1
2
m
kT
3
2
∫ (p ) ( )
2
0
h2e2 R 1
aff = 0.385
pm3 n3
2
mv
v exp –
dv
2kT
(
1
2
( )
2m
pkT
Quantum mechanical derivation by Gaunt is
modified by f-f Gaunt factor gf
)
III. Neutral Hydrogen: Free-Free Absorption
The absorption coefficient in square cm per neutral H
atom is proportional to the number density of
electrons, Ne and protons Ni:
k(Hff) =
afgfNiNe
N0
Density of neutral H
Recall the Saha Equation:
3
2
Ni
N
Pe =
Pe = NekT
( 2pm) ( kT)
h3
5
2
I
2u1(T)
exp –
kT
u0(T)
(
)
III. Neutral Hydrogen: Free-Free Absorption
3
2
k(Hff) = afgf
(2pmkT)
k(Hff) =
a0l3gf
Using:
I=hcR
h3
I
exp –
kT
(
log e
10–qI
2qI
R=2p2me4/h3c
q=log e/kT = 5040/T for eV
)
III. Total Absorption Coefficient for Hydrogen
total
bound-free
free-free
IV. The Negative Hydrogen Ion
The hydrogen atom is capable of holding a second
electron in a bound state.
The ionization of the extra electron requires 0.754 eV
All photons with l < 16444 Ang have sufficient
–
energy to ionize H back to neutral H
Very important opacity for Teff < 6000 K
Where does this extra electron come from?
Metals!
IV. The Negative Hydrogen Ion
For Teff > 6000 K, H– too frequently ionized to be an
effective absorber
For Teff < 6000 K, H– very important
For Teff < 4000 K, no longer effective because there
are no more free electrons
IV. The Negative Hydrogen Ion
The bound free absorption coefficient can be
expressed by the following polynomial
abf = a0 + a1l + a2l2 + a3l3 + a4l4 + a5l5 + a6l6
a0 = 1.99654
a1 = –1.18267 × 10–5
a2 = 2.64243 × 10–6
a3 = –4.40524 × 10–10
a4 = 3.23992× 10–14
a5 = –1.39568 × 10–10
a6 = 2.78701 × 10–23
l is in Angstroms
abf, 10–18 cm2 per H– ion
IV. The Negative Hydrogen Ion: Bound-Free
Wavelength (angstroms)
IV. The Negative Hydrogen Ion: bound-free
–
The H ionization is given by the Saha equation
N(H)
5040
–
–log
P
e
log N(H –) =
T I + 2.5 log T + 0.1248
in eV
u0(T) = 1, u1(T) = 2
–
5
2
k(Hbf ) = 4.158 × 10–10 abf Pe q 100.754q
IV. The Negative Hydrogen Ion: free-free
k(Hff = Peaff =
–)
10–26
× Pe 10
f0+f1logq+f2log2q
f0 = –2.2763–1.685 logl+0.766 log2l–0.0533464 log3l
f1 = 15.2827–9.2846 logl+1.99381 log2l–0.142631 log3l
f3 = –197.789+190.266 logl–67.9775 log2l+10.6913 log3l–0.625151 log4l
IV. The Negative Hydrogen Ion: Total
bound-free
free-free
V. The Negative Helium ion
The bound–free absorption is neglible, but free-free
can be important in the atmospheres of cool stars and
at longer wavelengths
VI. Metals
• In the visible a minor opacity source because
they are not many around
• Contribute indirectly by providing electrons
• In the visible kn(metals) ~ 1% kn(Hbf–)
• A different story in the ultraviolet where the
opacity is dominated by metals
VI. Metals
The absorption coefficient for metals dominate in the
ultraviolet
VII. Electron (Thompson) Scattering
• Important in hot stars where H is ionized
• Only true „grey“ opacity source since it
does not depend on wavelength
• Phase function for scattering ~ 1 + cos q
• Stellar atmosphere people assume average
phase ~ 0
VII. Electron (Thompson) Scattering
The absorption coefficient is wavelength independent:
(
(
8p
ae = 3
e2 2
–24 cm2/electron
=
0.6648
x
10
2
mc
The absorption per hydrogen atom:
k(e) =
aeNe
NH
=
aePe
PH
PH = Partial pressure of Hydrogen
VII. Electron (Thompson) Scattering
PH is related to the gas and electron pressure as
follows:
N = S Nj + Ne = NH S Aj + Ne
Nj particles of the jth element per cubic cm and Aj = Nj/NH
Solving for NH
NH =
N–Ne
S Aj
PH =
Pg–Pe
S Aj
VII. Electron (Thompson) Scattering
k(e) =
aePe S Aj
Pg– Pe
Electron scattering is important in O and Early B stars
If hydrogen dominates their composition Pe = 0.5Pg
k(e) = ae S Aj
Independent of
pressure
PTot = Pe + Pg
Pe /PTot
0.5
Teff
VIII. Other Sources of Opacity
H2 molecules
• H2 (neutral) has no significant absorption in the visible
• H2+, H2– do have significant absorption
• H2+(bf) important in the ultraviolet, in A-type stars it is
~ 10% of H– bound-free opacity
• Peaks in opacity around l ≈ 1100 Å, is dominated by
the Balmer continuum below 3600 Å in most stars
• H2– (free-free) important in the infrared (cool stars)
and fills the opacity minimum of H– at 16400 Å
VIII. Other Sources of Opacity
He I (bound-free), He II (bound-free)
• Important only in O and B-type stars
• He II (bound-free) is hydrogenic → multiply hydrogen
cross sections by Z4 or 16.
VIII. Other Sources of Opacity
Rayleigh Scattering
• Important in cool stars
• Scattering by molecules and atoms
• Has a 1/l4 dependence
VIII. Other Sources of Opacity
Cool Stars
• Molecules and ions:
CN–, C2–, H2, He, N2, O2, TiO,....
Basically Cool Stars are a mess and only for the
bravest theoretical astrophysicist
IX. Summary of Continuous Opacities
Spectral Type
Dominant opacity
O–B
Electron scattering, He I,II (b-f),
H(f-f)
B–A
H I: b-f, f-f
He II: b-f, some electron scattering
A–F
equal contributions from
H I (b-b) H I (f-f), H– (b-f, f-f)
G–K
H I (b-f), H– (b-f, f-f), Rayleigh
Scattering off H I
IX. Summary of Continuous Opacities
Spectral Type
Dominant opacity
K–Early M
H– (b-f, f-f), Rayleigh scattering
(UV) off H I and H2, molecular
opacities (line blanketing)
M:
Molecules and neutral atoms,
H– (b-f, f-f), Rayleigh scattering
off other molecules
Changes in the continuous opacity is the cause of most, if
not all pulsating stars
k Mechanism:
If in a region of the star the opacity changes, then the star can block energy
(photons) which can be subsequently released in a later phase of the pulsation.
Helium and and Hydrogen ionization zones of the star are normally where this
works. Consider the Helium ionization zone in the interior of a star. During a
contraction phase of the pulsations the density increases causing He II to
recombine. Neutral helium has a higher opacity and blocks photons and thus
stores energy. When the star expands the density decreases and neutral helium
is ionized by the emerging radiation. The opacity then decreases.
Cepheid Pulsations are due to an opacity effect:
Contraction
Expansion
He II/He III
ionization zone
During compression He II ionized to
He III, He III has a higher opacity. This
blocks radiation causing star to expand
During expansion He zone cools, He III
recombines, opacity decreases allowing
photons to escape. Star then contracts
under gravity.
Most pulsating stars can be explained by opacity effects
The End….our only friend the End