Download Andrej Cadez - UCLA Physics & Astronomy

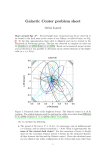
Tidal energy release before
plunging into a black hole
Andrej Čadež
Colaborators
Uroš Kostić
Massimo Calvani
Andreja Gomboc
Andrej Čadež
Uroš Kostić
Massimo Calvani
What would it look like if a light bulb
would be dropped into a black hole?
A far observer, more or less in the
orbital plane would see a signal like:
(Note that typical time scales are about 50M = 1000s for GCBH)
Sending a “realistic” object down a black hole
Observations of
flares from Galactic
center came as an
intriguing surprise;
they not only look
similar, but also
time scales match
• Some sort of a
“comet”,15 106km
long with
brightness
decreasing
exponentially from
head to tail and
exponentially
heating on a
plunging orbit
down the black
hole, would
produce a light
curve that is
strikingly similar to
the first IR flare
observed from the
Galactic center.
Energetics and time scales:
• Typical flare energy ~ 1035erg
• Flare rate
~ 1 /day
Remarkable facts:
1. almost a solar luminosity is turned on in less then
1000s; the turning off is just as fast
2. quasi-periods strongly suggest orbital motion very near
the black hole; accretion into the black hole is almost
inevitable
3. mass involved in producing a single flare could not be
very large: ~1020 g is consistent with the estimated
mass rate and produced energy, but requiering a few
percent mass to energy conversion efficiency.
Dilemma:
Disk oscillations – individual accretion events
• If flares are produced by magnetized disk oscillations,
the magnetic field must be high enough to essentially
influence dynamics, i.e. ½ m0B2~rc2. For example, a
conservatively high field B=100gauss requires r to be
lower then 4.5 10-16g/cm3 and has to fill the volume
4p/3(13 rg)3 to contain a mass 1021g. Such a high volume
could hardly oscillate with a period of ~1000sec.
• If flares are individual accretion events, then quite dense
blobs of material must be brought on orbits finally ending
in the black hole, the blobs must sustain high tidal stress
almost until the last turn down in order not to be smeared
much before falling in.
Stars in the Galactic center
Density of OB supergiants at GC
Paumard et all 2006
If a radial distribution would be
assumed this surface density
would correspond to
n = 0.5 pc-3/(r/pc)3
The distribution extends down to
~0.01 pc (=1’’)
The central pc thus contains ~40
OB supergiants and should
contain more than 104 solar mass
stars if Salpeter function is the
same in GC.
The Kuiper belt still contains
some 108 asteroids larger than
10 kilometer
Roche radius with respect to GC black hole
for stars, planets and asteroids
Note:
0.01pc=5 104 rg
Tidal interaction and its influence
on orbital evolution – Hut diagrams
Time scales
• 
=rRoche/rp
Tidal evolution of the orbit in angular
momentum energy plane
and periastron-apastron evolution
Tidal evolution of Effective potential
as a function of time
Some light curves
Observer almost in the orbital plane
Observer almost perpendicular to orbital plane
Summary
• We favor single individual short duration accretion events (of ~1020g
objects) as explanation of Galactic center flares, opposed to disk hot
spots. The inner Galactic center contains ~104 stars, and a star like
the Sun has ~108 solid satellites with m>1018g.
• In our scenario the maximum emissivity occurs on the way down the
black hole beyond the ISCO orbit and, therefore, high angular
momentum of the black hole is not required to explain the quasiperiodic substructure of flairs.
• Magnetic fields required to explain the synchrotron nature of emitted
radiation and the observed polarization are a natural consequence
of magnetic flux conservation during the exponential stretching of
the accreting object.