Download Slide 1




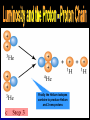
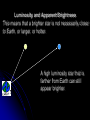
During the nineteenth
century, scientists
suggested that the Earth
was hundreds of millions
of years old.
Today we know the Earth
is 4.5 Billion years old.
PROBLEM – HOW CAN
THE SUN BURN SO HOT
FOR SO LONG A
TIME????

In the 1800’s Lord Kelvin and Hermann von
Helmholtz suggested that as gravity collapsed
the Sun, the gases would heat up. (KelvinHelmholtz contraction)



Kinda like a bicycle pump heats up compressed air.
PEgrav  Thermal Energy as star contracts
This process cannot be


Calculations show that the sun would have had to
start its contraction no more that 25 million years ago.
THE SOLAR SYSTEM IS MUCH, MUCH OLDER


A stars power output is called its LUMINOSITY.
What energy source produces this power???

Recall that Einstein
predicted that there is an
equivalence of mass and
energy according to
E = mc2

Consider the meaning of
this.

A small amount of mass
can release a tremendous
amount of energy
Fusion Requires Extreme
Conditions
Fusion
occurs during collisions
 long
range electrostatic forces work to keep
positively charged nuclei apart
 if nuclei come sufficiently close to one
another, the stronger but shorter range
nuclear forces work to pull nuclei together
requires high
temperatures: ~10 million K
 so
that particles have the velocities or
energies required to overcome electrostatic
repulsion
 the higher the electrostatic force the harder a
species is to fuse
Fusion
 so
requires high densities
that collisions are very common
Repulsive Force
Fusion
Strong electrostatic repulsion
at intermediate separation.
Particle Separation
Strong nuclear attraction at
very small separation.
Figure from Foundations of Astronomy by M. Seeds
The mass
defect is
converte
d into
energy
Positron –
electron
annihilation
Each proton
has a certain
mass
The resulting
Hydrogen atom
is less massive.
Note that one of
the protons
converted into a
neutron
A gamma ray
is given off
Another proton can now
combine with deuterium to
form a low mass isotope of
Helium
Fusion and Mass Defect

Consider this,
If 1kg of Hydrogen is converted into Helium, the
helium will have a mass of 993 grams.
The mass defect is converted to 6.3 x 1014J of
energy.
(like burning 20,000,000 kg of coal)
Finally the Helium isotopes
combine to produce Helium
and 2 new protons

Consider
the picture

Recall
Hydrostatic
Pressure

Now consider a “slab”
of solar material. Aka
a layer of the Sun.

The Suns interior is in
hydrostatic
equilibrium.

In general there is a
balance between


Radiation pressure and
Gravitational pressure
Each layer of a star is in thermal
equilibrium. Otherwise the star
would become too hot or too cold.
ENERGY MUST BE
TRANSPORTED TO THE
SURFACE by radiative diffusion
and convection
A diagram of
the Sun

All stars have a certain
Luminosity (L)

Power output in Watts

This information can tell
us a lot about a stars
history and current state.

First we need to
understand the inverse
square nature of EM
radiation.
d=1
B=1
d=2
B=1/4
d=3
B=1/9

How does the amount of paint caught by a 1
square unit area change with distance?
LUMINOSITY = THE AMOUNT OF ENERGY EMITTED
IN 1 SECOND
IF YOU DIVIDE THE LUMINOSITY BY THE SURFACE
AREA OF A SPHERE (where the detector would
be)YOU GET...
(PSRT)
L
b
4d 2
"Apparent Brighness"
[W m-2 ] or [J s-1m-2 ]

EXAMPLE PROBLEM
A long time ago in a galaxy far
far away
Darth Vader is observing two different stars.
Both stars are equally bright as observed from
his location, but Star A is 10 pc away and star B
is 20 pc away.
Which star is more luminous? By how much?
Summary - Luminosity and Brightness
Luminosity is an absolute value that measures the total
power radiated by a star. Luminosity is measured in
watts and tells us the rate that energy radiates from a
star in all directions. Our Sun has a luminosity of about
3.90 x 1026 W. Luminosity is very important in
providing information about star structure and age.
Apparent brightness is a relative value. As observers
on Earth, we perceive star brightness as the fraction of
the luminosity received by us. We measure brightness
in watts per square meter.
Luminosity and Apparent Brightness
Apparent Brightness
L
b
2
4 d
Apparent brightness depends on two variables:
Apparent brightness is proportional to the
luminosity of the star.
Apparent brightness is inversely proportional to
the square of the distance between the star
and the observer.
Luminosity and Apparent Brightness
This means that a brighter star is not necessarily closer
to Earth, or larger, or hotter.
A high luminosity star that is
farther from Earth can still
appear brighter.
Luminosity and Apparent Brightness
When comparing two stars the same distance from
Earth, the star with the greatest luminosity will appear
brighter.
Both the surface
temperature and size of
a star affect luminosity.
These relationships are
the topics of Wien’s and
the Stefan-Boltzmann
Laws
EXAMPLES

Tsokos 5ed - # 1-3 pg. 504