Download The Celestial Sphere - George Mason University

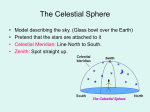
The Celestial Sphere
Lab 2
Celestial sphere
Geocentric model
• zenith - the point on the celestial sphere
that is directly over our heads always 90˚
from the horizon
• celestial meridian - the arc that goes
through the North point on the horizon,
Zenith, and South point on the horizon
Geocentric model
• All objects are slowly changing their
positions on the celestial sphere
• The only noticeable changes (for a human
lifespan) are diurnal and intrinsic motion
• Diurnal motion of celestial sphere – due to
earth’s rotation, does not change relative
positions
• Intrinsic motion – the “wanderers”
Ecliptic
• Ecliptic – “road of the sun”
– imaginary path that the Sun follows on the
celestial sphere over the course of a year
ecliptic
Celestial Coordinate System
• To measure distances on the imaginary
celestial sphere, we use angular
separations instead of miles/km
• There are 360˚ in a full circle and 90˚ in a
right angle
• Each degree is divided into 60 minutes of
arc
• Each minute of arc is divided into 60
seconds of arc
Celestial Coordinate System
• Sun and Moon are both ~0.5˚=30 arc min in
diameter
• The pointer stars in the bowl of the Big Dipper
are about 5˚ apart
• The arc from the N point on the horizon, through
the point directly overhead, to the S point on the
horizon is 180˚, so any object directly overhead
is 90˚ above the horizon
• Similarly any object ½-way up in the sky is ~45˚
above the horizon
NP
A
K
L
A
LA example details
• Los Angeles latitude 34° N.
• The NCP is therefore 34 degrees above the north
horizon.
• Because the Earth's equator is 90° away from the north
pole, the celestial equator as seen in LA will arc up to
90 - 34 = 56˚ above the southern horizon at the point it
crosses the meridian.
• It still intercepts the horizon due east and west.
• The stars rise in the E, move in arcs parallel to the
celestial equator reaching maximum altitude when they
cross your meridian, and set in the W part of the sky
• The star paths make an angle of 90 - 34 = 56˚ with
respect to the horizon.
animation
• http://www.star.ucl.ac.uk/~idh/STROBEL/n
akedeye/csph1t5.htm
Summary so far…..
• Meridian always goes through due North, zenith, and
due South points
• Altitude of zenith always equals 90°
• Altitude of celestial pole = observer's latitude. Observers
in northern hemisphere see NCP; observers in southern
hemisphere see SCP
• Altitude of celestial equator on meridian = 90 - observer's
latitude
• Celestial equator always intercepts horizon at due East
and due West points
• Angle celestial equator (and any star path) makes with
horizon = 90 - observer's latitude
• Stars move parallel to the celestial equator
RA
• Longitude lines run N-S
• Analogous celestial reference are lines of right
ascension
• RA is measured in hours, minutes, and seconds,
instead of degrees, and increases in an easterly
direction on the sky
• Zero RA is where the Sun crosses the celestial
equator
• The full 360 degrees circle is broken up into 24 hours,
so one hour of RA = 15 degrees.
• The lines of RA all converge at the celestial poles, so
two stars one hour of RA apart will not necessarily be
15 degrees in angular separation on the sky (only if
they are on the celestial equator will they be 15˚ apart)
Dec
• Latitude lines run E-W parallel to the equator
• When projected onto the sky, they become lines
of declination
• Like the latitude lines on Earth, declination (Dec)
is measured in degrees away from the celestial
equator, + for objects north of the celestial
equator and - for objects south of the celestial
equator
• Objects on the celestial equator are at 0˚ Dec
• objects ½-way to the NCP are +45˚
• objects at the NCP are +90˚
• objects at the SCP are -90˚
• Polaris's position is RA 2hr 31min, Dec +89˚ 15
arcmin
RA and Dec
Altitude and Azimuth
• Azimuth and altitude are usually used together to give
the direction of an object in the topocentric coordinate
system.
• We use altitude and azimuth to describe the location of
an object in the sky as viewed from a particular location
at a particular time.
• The altitude is the distance an object appears to be
above the horizon. The angle is measured up from the
closest point on the horizon.
• The azimuth of an object is the angular distance along
the horizon to the location of the object. By convention,
azimuth is measured from north towards the east along
the horizon
Altitude
• Altitude is the angle up from the horizon.
Zero degrees altitude means exactly on
your local horizon, and 90 degrees is
"straight up". Hence, "directly underfoot" is
-90 degrees altitude.
Azimuth
• Azimuth is the angle along the horizon,
with zero degrees corresponding to North,
and increasing in a clockwise fashion.
Thus, 90 degrees is East, 180 degrees is
South, and 270 degrees is West. Using
these two angles, one can describe the
apparent position of an object (such as the
Sun at a given time).
Azimuth
• We sometimes include the nearest compass
direction as an abbreviation to help clarify the
azimuth angles value in degrees. Up to three
letters are used and they represent azimuth
angles in the following order;
• N (0°), NNE (22.5°), NE (45°), ENE (67.5°), E
(90°), ESE (112.5°), SE (135°), SSE (157.5°), S
(180°), SSW (202.5°), SW (225°), WSW
(247.5°), W (270°), WNW (292.5°), NW (315°),
NNW (337.5°)
Horizontal Coordinate System
(Alt/Az coordinate system)
• The horizontal coordinates are:
• altitude (Alt), that is the angle between the object
and the observer's local horizon.
• azimuth (Az), that is the angle of the object
around the horizon (measured from the North
point, toward the East).
• The horizontal coordinate system is fixed to the
Earth, not the stars
• Used for determining the rise and set times of an
object in the sky.
• When an object's altitude is 0°, it is rising (if its
azimuth<180°) and setting (if its azimuth >180°)
Summary of Celestial Coordinates
for Positional Astronomy
• Altitude varies from 0 to 90°. Vertical position of
object
• Azimuth varies from 0° to 360°. Due N = 0°, due
E = 90°, due S = 180°, due W = 270°. Horizontal
position of object
• Right ascension varies from 0 to 24 hours.
Horizontal position of object.
• Declination varies from -90° (at SCP) to +90° (at
NCP). Celestial equator declination = 0°
• Meridian altitude of any object = 90 - (observer's
latitude) + declination degrees. If declination is
negative, then addition of declination becomes a
subtraction