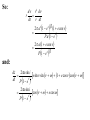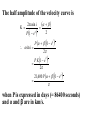Download binary stars instructor notes

Astronomy 2400
Physics of Stars
Examine basic properties of stars:
masses, luminosities, temperatures,
and chemical compositions, and how
they are established — the
observational method.
Examine the Sun as an example of a
typical nearby star — the nearest!
7. Binary Stars and Stellar Parameters
Goals:
1. Recognize different binary star types and
how each is observed.
2. Learn how stellar masses, luminosities,
and radii are measured using specific
binary star types.
3. Learn basic observational formulae for
the mass-luminosity relation and link
individual star types with specific masses.
Types: http://en.wikipedia.org/wiki/Binary_star
Optical double. Two physically unrelated stars
sharing a close coincidence in the line of sight.
Messier 20, the best known example of a line of sight
coincidence: separation 49".2 (1863), 51".7 (1966).
Inferred absolute magnitudes MV for the two stars:
+0.88, +4.0. Also known as Winnecke 4.
http://www.seds.org/messier/m/m040.html
Visual Binary. Two resolved, physically-related
stars sharing a very close spatial coincidence.
Beta Cygni (Albireo)
Changes in position angle for HD 30869.
Astrometric Binary. A single nearby star revealed
as a binary system from its periodic variations in
proper motion reflecting orbital motion about an
unseen companion.
The wobbling proper motion of Sirius — an
indication of orbital motion about a companion.
Eclipsing Binary. A single star revealed as a
binary system from the periodic mutual eclipses
of the two stars as they orbit each other with an
orbital plane lying nearly in the line of sight.
Primary
Minimum
Secondary
Minimum
V-band light curve for YY Sgr.
Spectrum Binary. A single star revealed as a
binary system from the presence of two distinct
spectral types in its spectrum — also referred to
as a composite spectrum binary.
Example spectra for a single hot subdwarf (top),
a composite hot subdwarf (middle), and a K1 V
standard (bottom).
Spectroscopic Binary. A single star revealed as a
binary system from periodic variations in in the
radial velocities measured from its spectral lines:
SB1 = one set of spectral lines detected, SB2 = two
sets of spectral lines detected, varying in velocity
out of phase with each other.
Spectral line shifts for a SB2.
Review: Properties of ellipses.
r = radius vector, foci = F, F', p = semiparameter
θ = position angle, P = periapsis, A = apapsis
e = eccentricity of orbital ellipse
Polar equation of orbit, above right.
Properties of ellipses, 2.
a = semi-major axis
b = semi-minor axis
c = centre distance = ae
Kepler’s eccentric circle, a circle inscribed on an
ellipse.
ν = true anomaly (called θ up until now)
E = eccentric anomaly
M = mean anomaly = 2π × Area in Yellow/πab
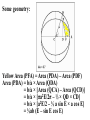
Some geometry:
Yellow Area (PFA) = Area (PDA) – Area (PDF)
Area (PDA) = b/a × Area (QDA)
= b/a × [Area (QCA) – Area (QCD)]
= b/a × [πa2E/2π – ½ × QD × CD]
= b/a × [a2E/2 – ½ a sin E × a cos E]
= ½ab (E – sin E cos E)
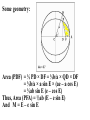
Some geometry:
Area (PDF) = ½ PD × DF = ½b/a × QD × DF
= ½b/a × a sin E × (ae – a cos E)
= ½ab sin E (e – cos E)
Thus, Area (PFA) = ½ab (E – e sin E)
And M = E – e sin E
The equation: M = E – e sin E
is called Kepler’s Equation, which relates the
eccentric anomaly E to the mean anomaly M.
M is simple to calculate since it represents the
amount of orbit swept out over a time interval t
relative to the orbital period P,
i.e. M = 2πt/P, where M is in radians.
M is therefore established by the time t. Once the
eccentricity e is established for an orbit, one can
calculate the eccentric anomaly E for time t using
Kepler’s equation. But the equation is not set up
for simple calculation. Instead, it is solved
iteratively.
Other equations that follow geometrically:
1
2


  1  e
E
 tan  
tan    
 2  1  e 
2
Kepler’s equation: M = E – e sin E
To solve this iteratively…
First reformulate: E = M + e sin E
Next rewrite it in an iterative form called the
Newton-Raphson Formula:
 M  Ei  e sin Ei 
Ei 1  Ei  

 1  e cos Ei 
Note: M and E are in radians.
Adopt E1 = M, solve for E2, substitute that value
into the equation for the next iteration, solve for
E3, then continue iterations until the series of Ei
values converge on a single value.
An example may help to illustrate the technique,
which is readily adapted for Excel.
Example: the orbital elements for the Sirius
binary system from a 1960 study are:
i = 136°.53
a = 7.500 arcseconds (*)
e = 0.592 (*)
ω = 44°.57
Ω = 147°.27
P = 50.090 years (*)
T = 1894.130 (*)
πabs = 0.37921 ±0.00158 arcsecond (Hipparcos) (*)
What is the separation of the two stars, in A.U.,
for 2007.1? Solution uses asterisked parameters.
Most recent periastron passage = 1894.130 + (2 ×
50.090) = 1994.31. So t = 2007.1 – 1994.31 = 12.79
years, or 2π × 12.79/50.090 = 1.604351 radians.
Thus, M = 1.604351 radians.
Successive iterations give:
E1 = 1.604351
E2 = 2.184496
E3 = 2.112776
E4 = 2.111807 (converged)
E5 = 2.111807
E6 = 2.111807
E7 = 2.111807 (fully converged)
Thus, tan(½ν) = (1.592/0.408)½ tan(½ × 2.111807)
= 1.9753381 × 1.7674087
= 3.4912297
And, ν = 2 × tan–1(3.4912297) = 148°.03318
r = a(1 – e2)/(1 + e cos ν)
a(A.U.) = a(")/π(") = 7.5/0.37921 = 19.777959A.U.
So, r = 19.777959(1 – 0.5922)/(1 + 0.592 cos 148°)
= 12.846497/(1 – 0.502226)
= 25.807894 A.U.
or
r = a(1 – e cos E)
So, r = 19.777959[1 – 0.592 cos (2.111807 rad)]
= 19.777959[1 – 0.592 cos (120°.99763)]
= 19.777959 × 1.3048815
= 25.807893 A.U.
i.e. r = 25.81 A.U.
Measurement of Visual Binaries:
separation = ρ (in arcseconds)
position angle = θ (in degrees)
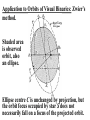
Application to Orbits of Visual Binaries: Zwier’s
method.
Shaded area
is observed
orbit, also
an ellipse.
Ellipse centre C is unchanged by projection, but
the orbit focus occupied by star S does not
necessarily fall on a focus of the projected orbit.
Line CS is portion of the
projected major axis
D1CSA1. Green lines
drawn parallel to D1CSA1
intersect apparent orbit
at ends of the projected
minor axis B1CE1. Or
obtain it by bisecting all
chords parallel to D1CSA1.
Project all chords parallel
to the projected minor axis
B1CE1 by the factor k = 1/(1 – e2)½ to get the
auxiliary ellipse. The auxiliary ellipse is the
projection of Kepler’s eccentric circle, so it can be
used to obtain the inclination angle i.
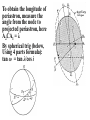
The auxiliary ellipse has a
semi-major axis A2C denoted
α and a semi-minor axis
B2C denoted β. Since it is the
projection of a circle, it
follows that:
a=α
cos i = β/α
Also:
e = ae cos i/a cos i = CS/CA1
To obtain k = 1/(1 – e2)½ .
So from geometry one can
find 3 orbital parameters:
i = orbital inclination
a = semi-major axis
e = orbital eccentricity
That leaves 4 additional
parameters to establish:
P = orbital period
T = time of periastron
passage (most recent)
ω = longitude of periastron (angle from node)
Ω = position angle of the node (descending
usually, ascending denoted by *)
Since the auxiliary ellipse is
Kepler’s eccentric circle
tilted through the angle i, the
axis A2CD2 represents the
line of nodes for the orbit.
So Ω = angle measured from
north (N) eastwards to the
nearest node, A2 as
illustrated here (reverse
view), otherwise D2. Radial
velocity data are needed to
establish whether it is the ascending (going into
the plane of the sky) or descending (coming out of
the plane of the sky) node.
To obtain the longitude of
periastron, measure the
angle from the node to
projected periastron, here
A2CA1 = λ
By spherical trig (below,
Using 4 parts formula):
tan ω = tan λ/cos i
The geometrical analysis therefore yields:
i = orbital inclination
a = semi-major axis
e = orbital eccentricity
ω = longitude of periastron
Ω = position angle of the node
The 2 remaining parameters,
P = orbital period
T = time of periastron passage (most recent)
are established from a temporal analysis of the
basic observations of separation and position
angle.
Spectroscopic Binaries:
Here it is necessary to establish the component of
one star’s orbit position along the line of sight.
sin x sin    

 sin    

sin i
sin 90
The radial velocity is the time derivative of that
component, plus the systemic motion of the
system, V0:
dz
d
VR  V0 
 V0  r sin    sin i 
dt
dt
The various components of the radial velocity are
evaluated with reference to the equation for the
areal constant, h:
d
dr
d
r sin      sin      r cos    
dt
dt
dt
dr d  a 1  e2    ae 1  e2 sin   d
 



dt dt  1  e cos   1  e cos 2  dt
 r 2e sin   d 2a e sin 


1
2 
2 2


a
1

e
dt


P 1  e 
2
1
dr
d

2

ab
2

a
2
2 2

Areal constant 
r


1 e 
dt
dt
P
P
So:
d r 2 d
r

dt
r dt
2 a 1  e  2 1  e cos 

P a 1  e 2 
2

1
2
2 a 1  e cos 
P 1  e
2

1
2
and:
dz
2a sin i

1 e sin  sin      1  e cos  cos    
dt P 1  e2 2
2a sin i

1 cos      e cos  
P 1  e2 2
If the constant terms are denoted as:
K 
then:
VR
2a sin i
P 1  e
2

1
2
 V0  K cos      e cos 
is the equation describing the radial velocity
variations of one star orbiting about another.
The radial velocity VR reaches a maximum value
when cos (ν + ω) = 1, i.e. ν + ω = 0° when the star
is entering the plane of the sky, and it reaches a
minimum value when cos (ν + ω) = –1, i.e. ν + ω =
180° when the star is exiting the plane of the sky.
Measured with respect to V0 maximum VR is
given by:
α = VR – V0 = K (1 + e cos ω),
while minimum VR is given by:
β = V0 – VR = K (1 – e cos ω).
So:
K = (α + β)/2 and e cos ω = (α – β)/(α + β)
Orbital Solutions: Lehmann-Filhés Method
Measured relative to V0:
z2
dz
Area A   dt  z2  z1
dt
z1
z3
dz
Area B   dt  z3  z2
dt
z2
But z3  z1 so Area A  Area B
V0 is therefore found either from planimetry or
mathematical integration software.
Points where VR –V0 = K[cos(ν + ω) + e cos ω] = 0
have cos(ν + ω) = –e cos ω, so:
 α  β 
cos       e cos  
α  β
Now integrate the velocity curve relative to the
points of inflection, which correspond to nodal
passage of the star: ascending node for maximum
VR (1) and descending node for minimum VR (3).
z2
dz
Area A1   dt  z2  z1  Z  0  Z
dt
z1
z3
dz
dt  z3  z2  0  Z   Z
dt
z2
Area A 2  
So Area A1  Area A 2  1
At 2, cos (ν + ω) = –e cos ω. Designate the true
anomaly at that point as ν1.
A positive sign applies since point 2 lies between
the ascending and descending nodes where z
reaches a maximum, i.e.
z2 = r1 sin (ν1 + ω) sin i
A minimum value for z is reached at point 4
where
z4 = r2 sin (ν2 + ω) sin i
 2 
And sin  2    
   
z2
dz
Area 1   dt  r1 sin  1   sin i
dt
z1
Area  2 
But

z1
dz
z dt dt   r2 sin  2   sin i
4
sin  2      sin  1   
1
r sin  1   sin i
r
 1
 1
 2  r2 sin  2   sin i r2
a 1  e 2 
Since r1 
and
1  e cos  1 
a 1  e 2 
r2 
1  e cos  2 
1 r1 1  e cos  2  1  e cos  2      

 

 2 r2 1  e cos  1  1  e cos  1      
1  e cos  2    cos   e sin  2   sin 

1  e cos  1    cos   e sin  1   sin 
2       e sin 

2       e sin 
From which
by substituti on
2    2  1 


e sin  
      2  1 
which, combined with the equation for e cos ω
yields a solution for both e and ω.
Periastron passage T occurs for ν = 0, in other
words for:
VR = V0 + K(1 + e) cos ω
which can be determined since K, e, ω and V0 are
known.
The possible ambiguity in where T falls in the
velocity curve is resolved by noting that (ν + ω)
= 0° at point 1 and (ν + ω) = 180° at point 3.
The orbital period P is established by curve
fitting to the radial velocity data, typically by
Fourier analysis or other similar techniques.
The half amplitude of the velocity curve is
K 
2a sin i
P 1  e
2

1
2

  

2
P    1  e
 a sin i 
2


P K 1  e
2
2
2

1
2

1
2
21,600 P    1  e
2

1
2

when P is expressed in days (= 86400 seconds)
and α and β are in km/s.
Some examples to illustrate how the velocity
curve depends upon the orbital parameters:
Parameters Obtained:
Double-lined systems.
M 1 a2 a2 sin i K 2



M 2 a1 a1 sin i K1
M 1  M 2 sin
3
i
1
2 3
1  e  K
2
3
2
1  K2 
 10.38 10 P 1  e
8
3
2
 K
3
2
1  K2 
3
Single-lined systems:
M 23 sin 3 i P 2
a1 sin i  
 M , the mass function
2
M 1  M 2 
3
3.993  1020 a1 sin i 

P2
3
Eclipsing Binaries:
Eclipse terminology:
Denote the larger star (usually the cooler star) as
star 1 and the smaller star (usually the hotter
star) as star 2.
A transit is an eclipse of star 1 by star 2, and can
be either annular or partial.
An occultation is an eclipse of star 2 by star 1 (the
deeper, primary eclipse) and can be either total or
partial.
The exact situation depends upon the inclination
of the orbit, i, and the radii of the two stars.
Complicating factors:
Stellar limb darkening.
Eccentric orbits.
Irradiation and ellipticity.
At present the light curves of eclipsing binaries
are analyzed using sophisticated computer
models that incorporate limb darkening,
ellipticity, and irradiation effects in a single
package, i.e. the Wilson-Devinney code.
A total eclipse
(occultation):
W Delphini.
The hotter star (more
radiant) is completely
covered at mid-eclipse,
leading to a flatbottomed light curve.
An annular eclipse
(transit):
YZ Cassiopeiae.
The hotter star (more
radiant) is larger than
the cooler star
(secondary), so is not
completely covered at
mid-eclipse, leading to
a round-bottomed
light curve.
The point α = 1
corresponds to what
we would term third
contact.
Planet transits of the
star HD 209458.
Note that the eclipses
are round-bottomed, a
result of limb
darkening on the star.
Summary:
Visual binaries give the sum of the masses of the
stars in a system. If a binary is resolved and close
enough for astrometry to detect the motion of the
system barycentre, the individual masses for the
stars can also be established. Luminosities can be
derived for systems of established distance.
Spectroscopic binaries place constraints on the
masses of stars in the system. SB1s give only a
mass function, while SB2s give mass ratios. An
eclipsing SB2 yields the masses of both stars,
since i is established.
Eclipsing binaries give the luminosities of both
stars in the system (from R and Teff), but only
yield masses if they are also SB2s.
Result:
A relationship between mass and luminosity of
stars, the ML relation, is established from the best
studied systems (Popper, 1980, ARAA, 18, 115).
When calibrated (Smith, 1983, Observatory, 103,
29) one obtains:
log L/Lsun = (3.99 ±0.03) log M/Msun M/Msun > 0.43
i.e. L ~ M4
log L/Lsun = (2.26 ±0.20) log M/Msun – (0.64 ±0.20)
M/Msun < 0.43, i.e. L ~ M2¼
A better calibration from Griffiths, Hicks &
Milone (1988, JRASC, 82, 1):
log L/Lsun = 4.20 sin (log M/Msun – 0.281) + 1.174
for angle argument in radians.
Note
turnover
Results for typical stars:
Main Sequence:
B0 V ~14 Msun
B5 V ~4 Msun
A0 V ~2.1 Msun
F0 V ~1.5 Msun
G2 V ~1.0 Msun
K0 V ~0.8 Msun
M0 V ~0.4 Msun
M supergiants ~15-25 Msun
O5 V ~ 32 Msun
K giants ~ 1-2 Msun
The most massive stars? Perhaps ~60 Msun
Note that the ML relation exists only for stars
lying near the main sequence.
Postscript:
Dynamical parallax, a technique used for binary
systems with dwarf components to estimate the
distance to the system.
 a "    1 
  2 
M 1  M 2   
  "    P 
a " 
so  dyn "   2
1
3
P M 1  M 2  3
3
Iterate beginning with (M1 + M2) = 1 or 2,
estimate πdyn from the above equation, evaluate
the luminosities of the stars in the system,
estimate new masses from the ML relation, and
continue until convergence.
Sample Problem:
Calculate the dynamical parallax for a visual binary system
consisting of two stars, both classified as spectral type G5 V
with magnitudes V = 6.26 and V = 6.36, having an orbital
period of P = 25.0 years and a semi-major axis a = 0".67.
Assume bolometric corrections of BC = –0.05 for G5 V stars
and that the system is close enough to be unreddened by
interstellar dust.
Solution:
From the equation for dynamical parallax,
a" 
0.67
 dyn " 1  2 3

 0.0621972
1
2
1
3
3
3
25.0 2.00
P M1  M 2 
So MV(1) = 6.26 + 5 log 0.0621972 + 5 = 5.23, Mbol(1) = 5.18
MV(2) = 6.36 + 5 log 0.0621972 + 5 = 5.33, Mbol(2) = 5.28
log L1 = [Mbol(Sun) – Mbol)]/2.5 = (4.79 – 5.18)/2.5 = –0.156
log L2 = [Mbol(Sun) – Mbol)]/2.5 = (4.79 – 5.28)/2.5 = –0.196
log M1 = log L1/3.99 = –0.156/3.99 = –0.0391, M1 = 0.914
log M2 = log L2/3.99 = –0.196/3.99 = –0.0491, M2 = 0.893
Our new estimate for M1 + M2 = 0.914 + 0.893 = 1.807 Msun
and
a " 
0.67
 dyn " 2 

 0.0643371
P
2
3
M1  M 2 
1
3
25.0 1.807
2
3
1
3
So MV(1) = 6.26 + 5 log 0.0643371 + 5 = 5.30, Mbol(1) = 5.25
MV(2) = 6.36 + 5 log 0.0643371 + 5 = 5.40, Mbol(2) = 5.35
log L1 = [Mbol(Sun) – Mbol)]/2.5 = (4.79 – 5.25)/2.5 = –0.184
log L2 = [Mbol(Sun) – Mbol)]/2.5 = (4.79 – 5.35)/2.5 = –0.224
log M1 = log L1/3.99 = –0.184/3.99 = –0.0461, M1 = 0.899
log M2 = log L2/3.99 = –0.224/3.99 = –0.0561, M2 = 0.879
Our new estimate for M1 + M2 = 0.899 + 0.879 = 1.778 Msun
and
a " 
0.67
 dyn " 3 

 0.064685
P
2
3
M1  M 2 
1
3
25.0 1.778
2
3
1
3
Further iterations give:
π1 = 0.0621972, π2 = 0.0643371, π3 = 0.064685, π4 = 0.0647336,
π5 = 0.0647824, π6 = 0.0647824 (converged)
So the dynamical parallax of the system is πdyn = 0".065.