Download Helyette Geman - slides - Oxford-Man Institute of Quantitative Finance

Commodity Forward Curves :
The Old and the New
Helyette Geman
Birkbeck, University of London & ESCP Europe
Member of the Board of the UBS- Bloomberg Commodity Index
To be presented at the Workshop on New Commodity Markets
Oxford Man Institute - June 13 to 15, 2011
Commodities and Shipping
→ They have existed as long as humankind, and will continue to be there for a long
time…
→ In the last 100 years, there have been a number of cycles of boom. The end of the
1970s boom can be identified with the crash in 1980 of precious commodities – and
the failure of the famous Hunt brothers’ squeeze of the silver market. Then
followed nearly 20 years of stagnation in commodity prices.
The 2000s decade started with gigantic rises in all commodity prices (at different
points in time across the years 2001 to 2005), witnessed the effect of the financial
crisis on commodities and a rebound afterwards.
As far as theory is concerned, commodities have been up to the late 1980s
essentially part of economic theory, with no major results coming from finance, and
contributions by economists called Keynes (1936), Kaldor (1939), Working (1949)
The Outlook of Commodity Markets in 2010
→ Increasing wealth invested in commodity indexes (DJ –UBS, GSCI, DB, RICI…)
→ Financial investors were usually positioned on the first nearby as the best to the spot
and avoid the hurdles of physical delivery and warehousing. Given the « noise » on
the first nearby and the frequent contango shape of the forward curve, they now go
to more and more distant maturities – which used to be the domain of action of the
specific industry. Hence, correlations and co- movements of the forward curve need
to be taken into account
→ Banks and private equity are buying physical assets, such as power plants, aluminium
smelters, which give them direct exposure to the spot price – in particular for
hedging activities.
→ At the same time, we witness a flurry of M&As, sometimes hostile, in the mining
industry worlwide, with some major actors being partly or fully state- owned
(Chinalco, Petrobras..)
m
ai
-9
oc 1
m t-91
ar
sao 92
ût
ja 92
nv
-9
ju 3
in
no 93
v9
av 3
r-9
se 4
pt
fé 94
vr
-9
ju 5
ildé 95
cm 95
ai
-9
oc 6
m t-96
ar
sao 97
ût
ja 97
nv
-9
ju 8
in
no 98
v9
av 8
rse 9 9
pt
-9
9
180
160
140
120
100
80
60
GSCI TR
DJ-AIGCITR
Growth of $100 invested in two major indexes during the period 1991-1999 :
Mean – Reversion in prices
ar
s00
ju
in
-0
se 0
pt
-0
dé 0
cm 00
ar
s01
ju
in
-0
se 1
pt
-0
dé 1
cm 01
ar
s02
ju
in
-0
se 2
pt
-0
dé 2
cm 02
ar
s03
ju
in
-0
se 3
pt
-0
dé 3
cm 03
ar
s04
m
190
170
150
130
110
90
GSCI TR
DJ-AIGCITR
Commodities as a Valuable Asset Class as of 2000
DJ – AIG Petroleum Index Dec 2001 - June 2006
500
450
400
350
300
250
200
150
100
50
1
3
5
7
9
11 13 15 17 19 21 23 25 27 29 31 33 35 37 39 41 43 45 47 49 51 53 55 57
DJ-AIG Petroleum Sub-index
Is Mean-Reversion Dead ? ( Geman - Sept 2005, J of
Alternative Investments )
CRB Commodity Index – 1990 to 2011
Commodity Prices: Back to Fundamentals
→ The price of a commodity is firstly driven by supply and demand
Quantity
Demand
Supply
Q°
P°
Supply
Demand
Price
Short-term inelastic supply and
demand
→ Another key quantity is the available inventory at the date of analysis, worldwide or
in a given region. This inventory has in impact on prices – hence, is carefully
watched by many CTAs (Commodity Trading Advisers) and on price volatility (see G Nguyen , Management Science, 2005).
→ For exhaustible commodities like crude oil, copper, gold.. reserves are the fourth key
quantity ultimately important
→ In contrast to financial markets, volume risk in commodity markets is as important as
price risk. Commodity markets (electricity, natural gas) have been used to handling
volume risk (Operational research, dynamic programming); financial markets are
used to price risk. The mathematical challenge today is to address both
simultaneously; the financial economics one is the market incompleteness, of various
degrees of profoundity.
Playing the WTI/ Brent spread while being “crude oil price neutral”
Theory of Storage
Keynes (1936), Kaldor (1939), Working (1949), Brennan (1958)
Four fundamentals results:
→ The convenience yield accounts for the benefit that accrues to the holder
of the physical commodity but not to the holder of the futures contract. It
is represented as an implicit dividend
→ The volatility of the commodity spot price is high when inventory is low
→ The volatility of Futures contracts decreases with the maturity:
"Samuelson effect“
→ Moreover, forward curves used to be viewed as being mostly in
backwardation, the so- called “normal backwardation”, due both to the
convenience yield and an assumption of mean- reversion in prices
Spot-Forward Relationship for a Storable Commodity
Under no arbitrage
⎤
⎡
f T (t ) = S(t ) ⎢ 1 + r ( T − t ) + c( T − t ) − y1 ( T − t ) ⎥
123
123
1
424
3 ⎥
⎢
⎣⎢ cos t of financing cos t of storage implicit dividend ⎥⎦
If we define a convenience yield net of cost of storage
f T (t ) = S(t )[1 + (r − y ) ( T − t )]
Or in continuous time, at a fixed date t for a given maturity T
f T (t ) = S(t ) e ( r − y )( T −t )
Correlation Spot- Prompt month (Nordpool):
The standard convenience yield does not apply to electricity
(Eydeland- G, RISK, 1998)
The Forward Curve
→ The set {FT (t) , T > t} is the forward curve prevailing at date t for a given
commodity in a given location
→ It is the fundamental tool when trading commodities, as spot prices may be
unabservable and options not always liquid
→ It allows to identify possible « carry arbitrage » : buy S, sell a future maturity T and
pay the cost of storage and financing as long as the net cashflow is strictly positive
→ The shape of the forward curve is at any date t in a one-to-one mapping with the
convenience yield y
→ It will reflect the seasonality in the case of seasonal commodities such as natural gas or
Agriculturals
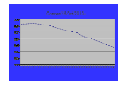
A typically backwardated commodity forward Curve - 27 May 2008
380
Copper COMEX
375
370
365
360
355
350
345
M1
M2
M3
M4
M5
M6
M7
M8
M9
M10
M11
M12
M13
M14
M15
M16
M17
M18
M19
M20
M21
M22
M23
M24
Copper Forward Curve, Oct 2009
Gold as a Numéraire Commodity
→ Historically, gold has been held as an international currency, independent
of individual countries.
→ At various times in history, domestic currencies have been backed by gold:
the “gold standard”
→ The unit of account of the International Monetary Fund (IMF) used to be
denominated in gold; now, a currency basket is used for indexation
→ Over the period following the financial crisis and up to now, gold is viewed
in all nations as a currency of intrinsic value and even as an “asset class”
→ Gold is traded in fine Troy ounces, ounces of actual gold in the ingot (there
are 32.15 Troy ounces in a kilo)
Contract months
déc-11
juin-11
déc-10
juin-10
déc-09
juin-09
déc-08
oct-08
août-08
juin-08
avr-08
févr-08
déc-07
oct-07
août-07
juin-07
mai-07
avr-07
mars-07
Price
COMEX Gold 28/2/2007
850
800
750
COMEX Gold
700
650
600
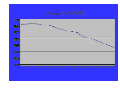
Gold Forward Curve - 27 May 2008
1100
Gold
1050
1000
950
900
850
800
M1
M2
M3
M4
M5
M6
M7
M8
M9
M10
M11
M12
M13
M14
M15
M16
M17
M18
Gold Forward Curve, October 26, 2009
Gold Forward Curve – Feb 2010
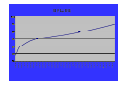
Number of Ounces of Gold that can buy the Average US House:
the Role of the Numéraire in the study of Commodities
Forward Curves and Inventories
→ The importance of inventory in explaining spot price volatility has been
widely documented in the economic literature
→ Brennan (1958) and Telser (1958) analyze in the context of several
agricultural commodities the spread between a long-term future and the
prompt month divided by the prompt month
→ They exhibit a negative correlation between this "relative spread" and the
variance of the commodity
→ Fama & French (1987) take as a given the property of the spread being
an adequate proxy for inventory. This allows them to analyze 21
commodities, including metals, for which good inventory data were
missing in their period of analysis
→ Ng & Pirrong (1994) examine four industrial and one precious metals
over the period 1986-1992 and use the same proxy for inventory to
conclude that fundamentals drive metal price dynamics
→ G. & Nguyen (2005) reconstruct a world database of soybean inventory
(with Brazil and Argentina having become more important than the US
in the last few years) and establish a quasi perfect affine relationship
between scarcity defined as inverse inventory and spot price volatility
Inventory and Forward Curve Adjusted Spread in Oil
and Natural Gas Markets
→ As said before, crude oil is not a seasonal commodity, natural gas is a very
seasonal commodity
→ G- Ohana (Energy Economics, 2009) choose the maturity of the “distant”
Future on criteria of liquidity and ability to filter out the seasonality
→ We used a price database consisting of daily NYMEX Futures prices
˜ for the oil from January 1990 to August 2006
˜ for natural gas from January 1993 to August 2006
→ We use for inventory data the EIA website
˜ for crude oil, we collect the volume of all stored petroleum products in
OECD countries at the end of each month from the end of December
1989 to the end of July 2006. This volume is expressed in billion barrels
for oil
˜ for natural gas, the website provides the volume of stored natural gas in
the United States at the end of each month during the period end of
December 1992 - end of July 2006
This inventory is expressed in Trillion cubic feet
0.2
0.0
-0.2
-0.4
gas relative spread
0.4
→ Using detrended inventory, it becomes
Rel-spread = 0.046 – 0.691 Inv
with
˜ Residual standard error = 0.092
˜ R² = 26%
1.5
2.0
deseasonalized gas inventory
2.5
Crude Oil Adjusted Spread vs Detrended Inventory
Crude Oil
Matthew Simmons, Twilight in the Desert
→ "Sooner or later, the worldwide use of oil must peak because oil, like the
other two fossils - coal and natural gas - is non renewable“
→ Over the past 30 years, daily oil consumption has risen by approximately 33
million barrels, Asia accounting for more than half of this growth in demand
→ Current consumption levels suggest that the world's oil supply should last
until around 2045 (without including tar sands)
→ The world's largest producers are Saudi Arabia (13% of world production),
Russia (12%), the United States (7%), Iran (6%) and China (5%)
→ The Gulf of Mexico region provides about 29% of the US oil production,
hence the disruption created by the long shutdown of many oil rigs after
hurricanes Katrina and Rita in summer 2005, and the recent rig accident
10/30/2007
7/10/2007
3/20/2007
11/28/2006
8/8/2006
4/18/2006
12/27/2005
9/6/2005
5/17/2005
1/25/2005
10/5/2004
6/15/2004
2/24/2004
11/4/2003
7/15/2003
3/25/2003
12/3/2002
8/13/2002
4/23/2002
1/1/2002
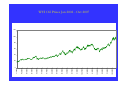
WTI Oil Prices Jan 2002 - Oct 2007
120
100
80
60
40
20
0
c9
av 5
rao 96
ût
-9
dé 6
c9
av 6
rao 97
ût
-9
dé 7
c9
av 7
rao 98
ût
-9
dé 8
c9
av 8
rao 99
ût
-9
dé 9
c9
av 9
rao 00
ût
-0
dé 0
c0
av 0
r
ao -01
ût
-0
dé 1
c0
av 1
r
ao -02
ût
-0
dé 2
c0
av 2
r
ao -03
ût
-0
dé 3
c0
av 3
r
ao -04
ût
-0
dé 4
c0
av 4
r-0
5
dé
Spread of the Oil Forward Curve - Dec 1995 / Dec 2005
Crude Oil Price Spread 29th Versus 1st
6
4
2
0
-2
-4
-6
-8
-10
-12
-14
Price Spread 29th Versus 1st
ar
s-
06
ju
il0
no 6
vm 06
ar
s07
ju
il0
no 7
vm 07
ar
s08
ju
il0
no 8
v
m -0 8
ar
s09
ju
il0
no 9
vm 09
ar
s10
ju
il1
no 0
vm 10
ar
s11
ju
il1
no 1
vm 11
ar
s12
ju
il1
no 2
vm 12
ar
s13
ju
il1
no 3
vm 13
ar
s14
ju
il14
m
Forward Price
Oil Forward Curve - March 2006 (Bid and Ask)
Forward Curv e
68,37
67,37
66,37
65,37
64,37
63,37
62,37
Maturity
WTI Forward Bid
WTI Forward Offer
Back to Backwardation in September 2007
80
78
76
74
72
70
68
M1
M5
M9
M13
M17
M21
M25
M29
M33
M37
M41
M45
M49
M53
M57
M61
Crude Oil Future curve (17/11/2008)
85
80
75
70
65
60
55
50
M1
M4
M7
M10
M13
M16
M19
M22
M25
M28
M31
M34
M37
M40
M43
M46
M49
M52
M55
M58
M61
Crude Oil Forward Curve – Feb 2010
References
H.Geman (2010) “Commodities and Numéraire”, Encyclopedia of Quantitative Finance
H. Geman and Yfong Shi (2009) “ The CEV model for Commodity Prices”, Journal of Alternative Investments
H. Geman and S. Kourouvakalis (2008) "A Lattice-Based Method for Pricing Electricity Derivatives under the GemanRoncoroni Model", Applied Mathematical Finance
H. Geman and C. Kharoubi( 2008) “Diversification with Crude Oil Futures : the Time-to- Maturity Effect, Journal of Banking
and Finance
S. Borovkova and H. Geman (2007) "Seasonal and Stochastic Effects in Commodity Forward Curves", Review of Derivatives
Research
H. Geman and A. Roncoroni (2006) "Understanding the Fine Structure of Electricity Prices", Journal of Business
H. Geman (2005) "Energy Commodity Prices: Is Mean Reversion Dead?", Journal of Alternative Investments
H. Geman and S. Ohana (2009) "Inventory, Reserves and Price volatility in Oil and Natural Gas Markets“,Energy Economics
H. Geman (2005) "Commodities and Commodity Prices: Pricing and Modelling for Agriculturals, Metals and Energy", Wiley
Finance
H. Geman and V. Nguyen (2005) "Soybean inventory and forward curves dynamics", Management Science
H.Geman (2004) “Water as the Next Commodity”, Journal of Alternative Investments
H. Geman and M. Yor (1993) "An Exact Valuation for Asian Option", Mathematical Finance
A. Eydeland and H. Geman (1999) "Fundamentals of Electricity options" in Energy Price Modelling, Risk Books
H. Geman and O. Vasicek (2001) "Forwards and Futures on Non Storable Commodities", RISK
H. Geman (2002) "Pure Jump Lévy Processes in Asset Price Modelling", Journal of Banking and Finance
H. Geman (2003) "DCF versus Real Option for Pricing Energy Physical Assets" Conference of the International Energy Agency - Paris
- March 2003
[email protected]