Download Lecture-2:Definition and Terminologies - Dr. Imtiaz Hussain

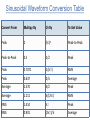
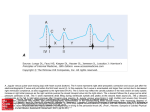
Power Electronics
Lecture-2
Definitions and Terminologies
Dr. Imtiaz Hussain
Assistant Professor
email: [email protected]
URL :http://imtiazhussainkalwar.weebly.com/
1
Measuring a Sine Wave
Peak value
• The PEAK value of the wave is the highest value the wave reaches
above a reference value.
• In a voltage waveform the peak value may be labelled VPK or
VMAX (IPK or IMAX in a current waveform).
c
c
c
c
c
2
Measuring a Sine Wave
Peak to Peak value
• The PEAK TO PEAK value is the vertical distance between the top
and bottom of the wave.
• It is measured in volts on a
voltage waveform, and may
be labelled VPP or VPK−PK.
• In a current waveform it
would be labelled IPP or
IPK−PK as I is used to represent
current.
3
Measuring a Sine Wave
Amplitude
• The AMPLITUDE of a sine wave is the maximum vertical distance
reached, in either direction from the centre line of the wave.
• As a sine wave is symmetrical about its centre line, the amplitude
of the wave is half the peak to peak value.
4
Measuring a Sine Wave
Periodic Time & Frequency
• The PERIODIC TIME is the time, in seconds taken for one complete cycle
of the wave.
• Thus if the periodic time of a wave is 20ms then there must be 50
complete cycles of the wave in one second (50Hz).
c
5
Measuring a Sine Wave
Average Value
• The average voltage (or current) of a periodic waveform whether it is
a sine wave, square wave or triangular waveform is defined as: “the
quotient of the area under the waveform with respect to time”.
• In other words, the averaging of all the instantaneous values along
time axis with time being one full period, (T).
𝑉1 + 𝑉2 + 𝑉3 + ⋯ + 𝑉11 + 𝑉12
𝑉𝑎𝑣 =
12
6
Measuring a Sine Wave
Average Value
• In a pure sine wave if the average value is calculated over the full
cycle, the average value would be equal to zero as the positive and
negative halves will cancel each other out.
• Then the average value is obtained by adding the instantaneous
values of voltage over one half cycle only.
1
𝑉𝑎𝑣 =
𝜋
𝜋
𝑉𝑝 sin 𝜃 𝑑𝜃
0
𝑉𝑝
𝑉𝑎𝑣 =
−cos 𝜃
𝜋
𝜋
0
2𝑉𝑝
𝑉𝑎𝑣 =
= 0.637𝑉𝑝
𝜋
7
Measuring a Sine Wave
RMS Value
Effective DC Value: RMS value gives the same heating effect as an
equivalent DC power.
𝑉𝑅𝑀𝑆 =
2
2
𝑉12 + 𝑉22 + 𝑉32 + ⋯ + 𝑉11
+ 𝑉12
12
8
Measuring a Sine Wave
𝑉𝑅𝑀𝑆 =
1
𝑇
𝑇
𝑉𝑃2 cos 2 (𝜔𝑡) 𝑑𝑡
𝑉𝑅𝑀𝑆 =
0
𝑉𝑅𝑀𝑆 =
𝑉𝑝
2
𝑉𝑃2
1
𝑡+
sin(2𝜔𝑡)
2𝑇
2𝜔
= 0.707𝑉𝑝
9
𝑇
0
Measuring a Sine Wave
INSTANTANEOUS VALUE
• The INSTANTANEOUS value of an alternating voltage or current is
the value of voltage or current at one particular instant.
• The value may be zero if the particular instant is the time in the
cycle at which the polarity of the voltage is changing.
• It may also be the same as the peak value, if the selected instant is
the time in the cycle at which the voltage or current stops
increasing and starts decreasing.
• There are actually an infinite number of instantaneous values
between zero and the peak value.
10
Measuring a Sine Wave
Form Factor
• The form factor of an alternating current waveform is the ratio of
the RMS value to the average value .
𝑉𝐹𝐹
𝑉𝑅𝑀𝑆
=
𝑉𝑎𝑣
• For a pure sinusoidal waveform the Form Factor will always be
equal to 1.11.
𝑉𝐹𝐹
0.707𝑉𝑝𝑘
=
= 1.11
0.637𝑉𝑝𝑘
11
Courtesy of Wikipedia
12
Measuring a Sine Wave
Crest Factor
• Crest Factor is the ratio between the R.M.S. value and the Peak
value of the waveform.
𝑉𝐶𝐹
𝑉𝑝𝑘
=
𝑉𝑅𝑀𝑆
• For a pure sinusoidal waveform the Crest Factor will always be
equal to 1.414.
•
Crest factor indicates how extreme the peaks are in a waveform.
• Both Form Factor and Crest Factor can be used to give information
about the actual shape of the AC waveform.
13
14
Courtesy of Wikipedia
Measuring a Sine Wave
Power Factor
• In an AC circuit, power is used most efficiently when the current is
aligned with the voltage.
• However, most equipment tend to draw current with a delay,
misaligning it with the voltage.
• What this means is more current is being drawn to deliver the
necessary amount of power to run the equipment. And the more
an equipment draws current with a delay, the less efficient the
equipment is.
15
Measuring a Sine Wave
Power Factor
• The power factor is the ratio of the real power that is used to do
work and the apparent power that is supplied to the circuit.
• The power factor can get values in the range from 0 to 1.
• When all the power is reactive power with no real power (usually
inductive load) - the power factor is 0.
• When all the power is real power with no reactive power (resistive
load) - the power factor is 1.
• The power factor is equal to the real or true power P in watts (W)
divided by the apparent power |S| in volt-ampere (VA):
𝑃𝑤𝑎𝑡𝑡
𝑃𝐹 =
𝑆𝑉𝐴
16
Importance of Power Factor
• A power factor of one or "unity power factor" is the goal of any
electric utility company since if the power factor is less than one,
they have to supply more current to the user for a given amount
of power use.
• Industrial facilities tend to have a "lagging power factor", where
the current lags the voltage (like an inductor).
• This is primarily the result of having a lot of electric induction
motors
• Capacitors have the opposite effect and can compensate for the
inductive motor windings.
• Some industrial sites will have large banks of capacitors strictly for
the purpose of correcting the power factor back toward one to
save on utility company charges.
17
A Sinusoidal Waveform
18
Formulae
Peak value of 𝑉 (𝑽𝒑 ) : As the name suggests 𝑉𝑝 = 𝑉 𝑚𝑎𝑥 over all time.
Average (DC) value of 𝑽 (𝑽𝒂𝒗 ): Assuming 𝑉 to be periodic over the time period 𝑇
then 𝑉𝑎𝑣 can be calculated as
1 𝑇
𝑉𝑎𝑣 =
𝑉 𝑑𝑡
𝑇 0
RMS (effective) value of 𝑽 (𝑽𝒓𝒎𝒔 ) : For 𝑉 , periodic over the time period 𝑇,
𝑉𝑟𝑚𝑠 =
1
𝑇
𝑇
𝑉 2 𝑑𝑡
0
Form factor of 𝑽 (𝑽𝑭𝑭 ) : Form factor of ‘𝑉 ‘ is defined as
𝑉𝐹𝐹
𝑉𝑟𝑚𝑠
=
𝑉𝑎𝑣
Power Factor (PF): As for any other equipment, the definition of the power factor of
a rectifier is
𝐴𝑐𝑡𝑢𝑎𝑙 𝑃𝑜𝑤𝑒𝑟 𝐼𝑛𝑝𝑢𝑡 𝑡ℎ𝑒 𝑅𝑒𝑐𝑡𝑖𝑓𝑖𝑒𝑟
𝑃𝐹 =
𝐴𝑝𝑝𝑎𝑟𝑒𝑛𝑡 𝑃𝑜𝑤𝑒𝑟 𝐼𝑛𝑝𝑢𝑡 𝑡𝑜 𝑡ℎ𝑒 𝑅𝑒𝑐𝑡𝑖𝑓𝑖𝑒𝑟
19
Sinusoidal Waveform Conversion Table
Convert From
Multipy By
Or By
To Get Value
Peak
2
(√2)2
Peak-to-Peak
Peak-to-Peak
0.5
1/2
Peak
Peak
0.7071
1/(√2)
RMS
Peak
0.637
2/π
Average
Average
1.570
π/2
Peak
Average
1.111
π/(2√2)
RMS
RMS
1.414
√2
Peak
RMS
0.901
(2√2)/π
Average
20
To download this lecture visit
http://imtiazhussainkalwar.weebly.com/
END OF LECTURE-2
21